山东省临沂市临沭县2021-2022学年八年级上学期期中数学试题
试卷更新日期:2021-12-01 类型:期中考试
一、单选题
-
1. 北京2022年冬奥会会徽如图所示,组成会徽的四个图案中是轴对称图形的是( )
 A、
A、 B、
B、 C、
C、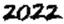 D、
D、 2. 将一副三角板按如图方式重叠,则 的度数为( )
2. 将一副三角板按如图方式重叠,则 的度数为( ) A、 B、 C、 D、3. 一个多边形的内角和是1260°,这个多边形的边数是( )A、6 B、7 C、8 D、94. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )
A、 B、 C、 D、3. 一个多边形的内角和是1260°,这个多边形的边数是( )A、6 B、7 C、8 D、94. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )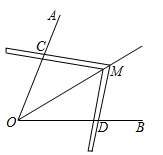 A、 B、 C、 D、5. 一条船从海岛A出发,以15海里/时的速度向正北航行,2小时后到达海岛B处.灯塔C在海岛A的北偏东43°方向上,在海岛B的北偏东86°方向上.则海岛B到灯塔C的距离是( )A、15海里 B、20海里 C、30海里 D、60海里6. 如图, ,过点A作 ,垂足为点F , 若 ,则 的度数为( )
A、 B、 C、 D、5. 一条船从海岛A出发,以15海里/时的速度向正北航行,2小时后到达海岛B处.灯塔C在海岛A的北偏东43°方向上,在海岛B的北偏东86°方向上.则海岛B到灯塔C的距离是( )A、15海里 B、20海里 C、30海里 D、60海里6. 如图, ,过点A作 ,垂足为点F , 若 ,则 的度数为( )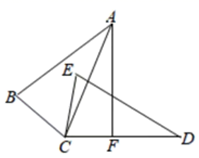 A、15° B、25° C、35° D、65°7. 如图,点B , F , C , E共线,∠B=∠E , BF=EC , 添加一个条件,不能判断△ABC≌△DEF的是( )
A、15° B、25° C、35° D、65°7. 如图,点B , F , C , E共线,∠B=∠E , BF=EC , 添加一个条件,不能判断△ABC≌△DEF的是( ) A、AB=DE B、∠A=∠D C、AC=DF D、AC∥FD8. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 .据此,可求得学校与工厂之间的距离 等于( )
A、AB=DE B、∠A=∠D C、AC=DF D、AC∥FD8. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 .据此,可求得学校与工厂之间的距离 等于( )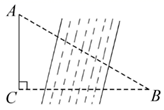 A、 B、 C、 D、9. 如图,点F在正五边形 的内部, 为等边三角形,则 等于( )
A、 B、 C、 D、9. 如图,点F在正五边形 的内部, 为等边三角形,则 等于( )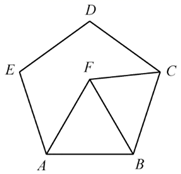 A、 B、 C、 D、10. 若定义: , ,例如 , ,则 =( )A、 B、 C、 D、11. 如果一等腰三角形的周长为27,且两边的差为12,则这个等腰三角形的腰长为( )A、13 B、5 C、5或13 D、112. 如图所示,H是 的高AD , BE的交点,且 ,则下列结论:① ;② ;③ ;④ .正确的有( )
A、 B、 C、 D、10. 若定义: , ,例如 , ,则 =( )A、 B、 C、 D、11. 如果一等腰三角形的周长为27,且两边的差为12,则这个等腰三角形的腰长为( )A、13 B、5 C、5或13 D、112. 如图所示,H是 的高AD , BE的交点,且 ,则下列结论:① ;② ;③ ;④ .正确的有( )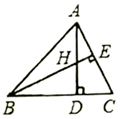 A、1个 B、2个 C、3个 D、4个13. 如图,在 的正方形网格中有两个格点A、B,连接 ,在网格中再找一个格点C,使得 是等腰直角三角形,满足条件的格点C的个数是( )
A、1个 B、2个 C、3个 D、4个13. 如图,在 的正方形网格中有两个格点A、B,连接 ,在网格中再找一个格点C,使得 是等腰直角三角形,满足条件的格点C的个数是( ) A、2 B、3 C、4 D、514. △BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长,则只需知道( )
A、2 B、3 C、4 D、514. △BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长,则只需知道( )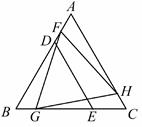 A、△ABC的周长 B、△AFH的周长 C、四边形FBGH的周长 D、四边形ADEC的周长
A、△ABC的周长 B、△AFH的周长 C、四边形FBGH的周长 D、四边形ADEC的周长二、填空题
-
15. 若长度分别为4,5,a的三条线段能组成一个三角形,则整数a的值可以是 . (写出一个即可)16. 如图,点A、B分别在x轴、y轴上, ,分别以点A、B为圆心,以大于 长为半径画弧,两弧交于点P . 若点P的坐标为 ,则a的值为 .
 17. 如图,在 中,BC的垂直平分线分别交BC、AB于点E、F . 若 cm, 周长为12cm,则 的周长为cm.
17. 如图,在 中,BC的垂直平分线分别交BC、AB于点E、F . 若 cm, 周长为12cm,则 的周长为cm. 18. 如图,在 中, , ,以点C为圆心,CA长为半径作弧,交直线BC于点P , 连接AP , 则 的度数是 .
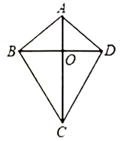
18. 如图,在 中, , ,以点C为圆心,CA长为半径作弧,交直线BC于点P , 连接AP , 则 的度数是 . 19. 如图,在四边形ABCD中, , ,对角线AC , BD相交于点O , 下列结论中:
19. 如图,在四边形ABCD中, , ,对角线AC , BD相交于点O , 下列结论中:① ;②AC垂直平分BD;③AC平分 , ;④BD平分 , ;⑤四边形ABCD的面积 .正确的是 . (填写所有正确结论的序号)
三、解答题
-
20. 如图, 中,CD平分 , , .求 , 的度数.
 21. 生活中处处有数学.
21. 生活中处处有数学. (1)、如图(1)所示,一扇窗户打开后,用窗钩 将其固定,这里所运用的数学原理是;(2)、如图(2)所示,在新修的小区中,有一条“ ”字形绿色长廊 ,其中 ,在 , , 三段绿色长廊上各修一小凉亭 , , ,且 ,点 是 的中点,在凉亭 与 之间有一池塘,不能直接到达,要想知道 与 之间的距离,只需要测出线段 的长度,这样做合适吗?请说明理由.22. 如图,在 中, , .
(1)、如图(1)所示,一扇窗户打开后,用窗钩 将其固定,这里所运用的数学原理是;(2)、如图(2)所示,在新修的小区中,有一条“ ”字形绿色长廊 ,其中 ,在 , , 三段绿色长廊上各修一小凉亭 , , ,且 ,点 是 的中点,在凉亭 与 之间有一池塘,不能直接到达,要想知道 与 之间的距离,只需要测出线段 的长度,这样做合适吗?请说明理由.22. 如图,在 中, , . (1)、通过观察尺规作图的痕迹,可以发现直线DF是线段AB的 , 射线AE是 的;(2)、在(1)所作的图中,求 的度数.23. 在平面直角坐标系中的位置如图所示,A、B、C三点在格点上,点B的坐标为 .
(1)、通过观察尺规作图的痕迹,可以发现直线DF是线段AB的 , 射线AE是 的;(2)、在(1)所作的图中,求 的度数.23. 在平面直角坐标系中的位置如图所示,A、B、C三点在格点上,点B的坐标为 .
( 1 )作出 关于x轴对称的 ,并写出点 的坐标;
( 2 )作出 关于y轴对称的 ,并写出点 的坐标,
24. 如图,在四边形ABCD中, ,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证: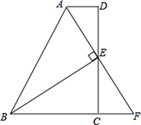 (1)、FC=AD;(2)、AB=BC+AD.
(1)、FC=AD;(2)、AB=BC+AD.