山东省临沂市莒南县2021-2022学年八年级上学期期中数学试题
试卷更新日期:2021-12-01 类型:期中考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是 ( )
 A、①⑤ B、②⑤ C、④⑤ D、①③2. 如图,在 中, 边上的高为( )
A、①⑤ B、②⑤ C、④⑤ D、①③2. 如图,在 中, 边上的高为( ) A、 B、 C、 D、3. 如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°……照这样走下去,他第一次回到出发点A时,共走路程为( )
A、 B、 C、 D、3. 如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°……照这样走下去,他第一次回到出发点A时,共走路程为( ) A、80米 B、96米 C、64米 D、48米4. 如图,△ABC △DEF,点E,C,F,B在同一条直线上.下列结论正确的是( )
A、80米 B、96米 C、64米 D、48米4. 如图,△ABC △DEF,点E,C,F,B在同一条直线上.下列结论正确的是( ) A、 B、 C、 D、5. 如图,在 ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列结论错误的是( )
A、 B、 C、 D、5. 如图,在 ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列结论错误的是( ) A、AD平分∠BAC B、∠ADC=60° C、点D在AB的垂直平分线上 D、 =1:26. 已知三角形两边的长分别是5和9,则此三角形第三边长可能是( )A、1 B、4 C、8 D、147. 一个多边形的内角和等于它的外角和的3倍,则它是( )边形.A、六 B、七 C、八 D、九8. 如图,在正方形 的外侧,作等边三角形 ,则 为( )
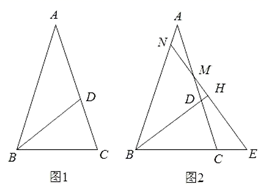
A、AD平分∠BAC B、∠ADC=60° C、点D在AB的垂直平分线上 D、 =1:26. 已知三角形两边的长分别是5和9,则此三角形第三边长可能是( )A、1 B、4 C、8 D、147. 一个多边形的内角和等于它的外角和的3倍,则它是( )边形.A、六 B、七 C、八 D、九8. 如图,在正方形 的外侧,作等边三角形 ,则 为( )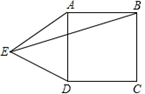 A、45° B、25° C、30° D、40°9. 如图,AD是△ABC的中线,E , F分别是AD和AD延长线上的点,且DE=DF , 连接BF , CE , 下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE . 其中正确的是( )
A、45° B、25° C、30° D、40°9. 如图,AD是△ABC的中线,E , F分别是AD和AD延长线上的点,且DE=DF , 连接BF , CE , 下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE . 其中正确的是( ) A、①② B、①③ C、①③④ D、①④⑤10. 如图,△ABC的面积为9cm2 , BP平分∠ABC , AP⊥BP于P , 连接PC , 则△PBC的面积为( )
A、①② B、①③ C、①③④ D、①④⑤10. 如图,△ABC的面积为9cm2 , BP平分∠ABC , AP⊥BP于P , 连接PC , 则△PBC的面积为( ) A、3cm2 B、4.5cm2 C、5cm2 D、6cm211. 如图,若MB=ND , ∠MBA=∠NDC , 下列条件中不能判定 的是( )
A、3cm2 B、4.5cm2 C、5cm2 D、6cm211. 如图,若MB=ND , ∠MBA=∠NDC , 下列条件中不能判定 的是( ) A、AM=CN B、 C、AB=CD D、∠M=∠N12. 如图, 中, , , , 于点 , 是 的垂直平分线,交 于点 ,交 于点 ,在 上确定一点 ,使 最小,则这个最小值为( )
A、AM=CN B、 C、AB=CD D、∠M=∠N12. 如图, 中, , , , 于点 , 是 的垂直平分线,交 于点 ,交 于点 ,在 上确定一点 ,使 最小,则这个最小值为( ) A、3.5 B、4 C、4.5 D、513. 下列给出的5个图中,能判定 是等腰三角形的有( )
A、3.5 B、4 C、4.5 D、513. 下列给出的5个图中,能判定 是等腰三角形的有( ) A、2个 B、3个 C、4个 D、5个14. 如图,在 的网格中,每一个小正方形的边长都是1,点 , , , 都在格点上,连接 , 相交于 ,那么 的大小是( )
A、2个 B、3个 C、4个 D、5个14. 如图,在 的网格中,每一个小正方形的边长都是1,点 , , , 都在格点上,连接 , 相交于 ,那么 的大小是( )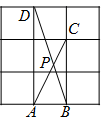 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
15. 如图,在 中,DE垂直平分BC交AB于点E , 若 , 的周长为31,则 的周长为 .
 16. 如图,△ABC中,∠C=90°,AD平分∠CAB , 且BC=12cm , BD=8cm , 则点D到AB的距离为cm .
16. 如图,△ABC中,∠C=90°,AD平分∠CAB , 且BC=12cm , BD=8cm , 则点D到AB的距离为cm . 17. 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为秒时,△ABP和△DCE全等.
17. 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为秒时,△ABP和△DCE全等. 18. 如图,∠ACB=90°,AC=BC , AD⊥CE于点D , BE⊥CD交CD的延长线于点E , AD=2.4 cm,DE=1.7 cm,则BE的长为 .
18. 如图,∠ACB=90°,AC=BC , AD⊥CE于点D , BE⊥CD交CD的延长线于点E , AD=2.4 cm,DE=1.7 cm,则BE的长为 . 19. 如图,已知 ,点 , , , 在射线ON上,点 , , , 在射线OM上, , , , 均为等边三角形,若 ,则 的边长为 .
19. 如图,已知 ,点 , , , 在射线ON上,点 , , , 在射线OM上, , , , 均为等边三角形,若 ,则 的边长为 .
三、解答题
-
20. 如图,
 (1)、画出△ABC关于y轴的对称图形△A1B1C1;(2)、直接写出△ABC关于x轴对称的三角形△A2B2C2的各点坐标.21. 如图,在 中, , 分别是 的高和角平分线,若 , ,求 的度数.
(1)、画出△ABC关于y轴的对称图形△A1B1C1;(2)、直接写出△ABC关于x轴对称的三角形△A2B2C2的各点坐标.21. 如图,在 中, , 分别是 的高和角平分线,若 , ,求 的度数. 22. 如图,已知等边 分别在 上,且 ,连接 交 点.求证:
22. 如图,已知等边 分别在 上,且 ,连接 交 点.求证: 23. 如图,在 中, , ,点 在边 上,点 , 在线段 上,且 , .若 的长为5,求 的长.
23. 如图,在 中, , ,点 在边 上,点 , 在线段 上,且 , .若 的长为5,求 的长. 24. 如图,在 中, , 分别是 , 的角平分线.
24. 如图,在 中, , 分别是 , 的角平分线. (1)、若 , ,则 的度数是;(2)、探究 与 的数量关系,并证明你的结论.
(1)、若 , ,则 的度数是;(2)、探究 与 的数量关系,并证明你的结论.