辽宁省鞍山市铁西区2021-2022学年八年级上学期期中数学试题
试卷更新日期:2021-12-01 类型:期中考试
一、单选题
-
1. 下列式子正确的有( )个.
⑴(a+1)2=a2+1
⑵(3x2y+xy)+xy=3x
⑶(﹣2ab2)3=8a3b6;
⑷(1﹣x)2(x﹣1)2=(1﹣x)4
⑸(﹣a+b)(b﹣a)=a2﹣b2
A、1 B、2 C、3 D、42. 小明用长度分别为5,a,9的三根木棒首尾相接组成一个三角形,则a可能是( ).A、 B、 C、 D、3. 要使分式 有意义,实数a必须满足( )A、a=2 B、a=﹣2 C、a≠2 D、a≠2且a≠﹣24. 如图,用三角板作 的边 上的高线,下列三角板的摆放位置正确的是( )A、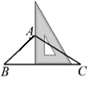 B、
B、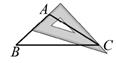 C、
C、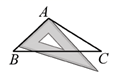 D、
D、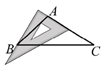 5. 已知xa=4,xb=5,则x3a﹣2b等于( )A、 B、 C、 D、6. 若一个多边形的内角和为 ,则从该多边形的一个顶点出发的对角线条数是( )A、3 B、4 C、5 D、67. 下列四个整式:①x2﹣4x+4;②6x2+3x+1;③4x2+4x+1;④x2+4xy+2y2 . 其中是完全平方式的是( )A、①③ B、①②③ C、②③④ D、③④8. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC , AB于点M , N . 再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧交于点P , 作射线AP交边BC于点D . 若CD=3,AB=10,则△ABD的面积是( )
5. 已知xa=4,xb=5,则x3a﹣2b等于( )A、 B、 C、 D、6. 若一个多边形的内角和为 ,则从该多边形的一个顶点出发的对角线条数是( )A、3 B、4 C、5 D、67. 下列四个整式:①x2﹣4x+4;②6x2+3x+1;③4x2+4x+1;④x2+4xy+2y2 . 其中是完全平方式的是( )A、①③ B、①②③ C、②③④ D、③④8. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC , AB于点M , N . 再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧交于点P , 作射线AP交边BC于点D . 若CD=3,AB=10,则△ABD的面积是( ) A、10 B、15 C、30 D、209. 若c2﹣a2﹣2ab﹣b2=10,a+b+c=﹣5,则a+b﹣c的值是( )A、2 B、5 C、20 D、910. 如图,△ABC中,∠ACF、∠EAC的角平分线BP、AP交于点P , 延长BA、BC , PM⊥BE , PN⊥BF . 则下列结论中:①BP平分∠ABC;②∠ABC+2∠APC=180°;③∠CAB=2∠CPB;④S△PAC=S△MAP+S△NCP . 正确的个数( )
A、10 B、15 C、30 D、209. 若c2﹣a2﹣2ab﹣b2=10,a+b+c=﹣5,则a+b﹣c的值是( )A、2 B、5 C、20 D、910. 如图,△ABC中,∠ACF、∠EAC的角平分线BP、AP交于点P , 延长BA、BC , PM⊥BE , PN⊥BF . 则下列结论中:①BP平分∠ABC;②∠ABC+2∠APC=180°;③∠CAB=2∠CPB;④S△PAC=S△MAP+S△NCP . 正确的个数( )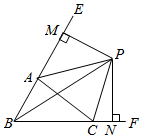 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 计算(﹣0.125)2020×82021的结果是 .12. 在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°-∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有(填序号)13. 已知(a﹣b)2=6,(a+b)2=4,则a2+b2的值为 .14. 如图,∠E=∠F=90°,∠B=∠C , AE=AF , 给出下列结论:①∠1=∠2;②CM=BN;③△ACN≌△ABM;④MD=EM . 其中正确的结论是 (填序号).
 15. (x2﹣mx+6)(4x﹣2)的积中不含x的二次项,则m的值是 .16. 如图所示,若∠DBE=78°,则∠A+∠C+∠D+∠E= .
15. (x2﹣mx+6)(4x﹣2)的积中不含x的二次项,则m的值是 .16. 如图所示,若∠DBE=78°,则∠A+∠C+∠D+∠E= . 17. 计算20212﹣2025×2017= .18. 如图,已知等腰Rt△ABC中,AB=AC , ∠BAC=90°,点A , B分别在x轴和y轴上,点C的坐标为(4,1),则B点坐标为 .
17. 计算20212﹣2025×2017= .18. 如图,已知等腰Rt△ABC中,AB=AC , ∠BAC=90°,点A , B分别在x轴和y轴上,点C的坐标为(4,1),则B点坐标为 .
三、解答题
-
19. 计算与分解因式
计算:
(1)、(2x2y)2•(﹣5xy2)÷(14x4y3)(2)、(x+y﹣m+n)(x﹣y﹣m﹣n).(3)、16x4﹣1;(4)、(a﹣b)(5a+2b)+(a+6b)(b﹣a).20. 如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O , ∠CAB=50°,∠BOA=120°,求∠DAE和∠C的度数. 21. 先化简,再求值:[(2x﹣2y)(x+y)﹣2(x﹣y)2+3y(x﹣y)]÷(4y),其中x=2,y=4.22. 如图,在△AOB和△COD中,OA=OB , OC=OD(OA<OC),∠AOB=∠COD=α,直线AC , BD交于点M , 连接OM , 求证:∠OAM=∠OBM .
21. 先化简,再求值:[(2x﹣2y)(x+y)﹣2(x﹣y)2+3y(x﹣y)]÷(4y),其中x=2,y=4.22. 如图,在△AOB和△COD中,OA=OB , OC=OD(OA<OC),∠AOB=∠COD=α,直线AC , BD交于点M , 连接OM , 求证:∠OAM=∠OBM . 23. 如图,在△ABC中,点E , F分别为AC , AB上的点,连接DE , DF , 且∠BAC+∠EDF=180°.
23. 如图,在△ABC中,点E , F分别为AC , AB上的点,连接DE , DF , 且∠BAC+∠EDF=180°. (1)、求证:∠AFD=∠BED;(2)、若DE=DF请说明AD平分∠BAC .24. 数学教科书中这样写道:“我们把多项式a2+2ab+b2及a2﹣2ab+b2叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:
(1)、求证:∠AFD=∠BED;(2)、若DE=DF请说明AD平分∠BAC .24. 数学教科书中这样写道:“我们把多项式a2+2ab+b2及a2﹣2ab+b2叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等.
例如:分解因式x2+2x﹣3=(x2+2x+1)﹣4=(x+1)2﹣4=(x+1+2)(x+1﹣2)=(x+3)(x﹣1);例如求代数式2x2+4x﹣6的最小值,2x2+4x﹣6=2(x2+2x﹣3)=2(x+1)2﹣8,可知当x=﹣1时,2x2+4x﹣6有最小值,最小值是﹣8.
根据阅读材料用配方法解决下列问题:
(1)、分解因式:m2﹣4m﹣5= .(2)、求代数式x2+2x+4的最小值.(3)、已知a、b、c是△ABC的三边长,且满足a2+c2+2b(b﹣a﹣c)=0,试判断△ABC的形状.25. 已知:CD是经过∠BCA的顶点C的一条直线,CA=CB , E、F是直线CD上两点,∠BEC=∠CFA=∠α.(1)、若直线CD经过∠BCA的内部,∠BCD>∠ACD .①如图1,∠BCA=90°,∠α=90°,写出BE , EF , AF间的等量关系: .
②如图2,∠α与∠BCA具有怎样的数量关系,能使①中的结论仍然成立?写出∠α与∠BCA的数量关系 .
(2)、如图3.若直线CD经过∠BCA的外部,∠α=∠BCA , ①中的结论是否成立?若成立,进行证明;若不成立,写出新结论并进行证明.