江西省赣州市2021-2022学年八年级上学期期中数学试题
试卷更新日期：2021-12-01 类型：期中考试
一、单选题
-
1. 下列四个腾讯软件图标中，属于轴对称图形的是（ ）A、
B、
C、
D、
2. 如图，∠1＝120°，∠E＝80°，则∠A的大小是（ ）
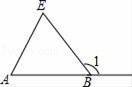A、10° B、40° C、30° D、80°3. 如图，已知：AC＝DF ， AC∥FD ， AE＝DB ， 判断△ABC≌△DEF的依据是（ ）
A、SSS B、SAS C、ASA D、AAS4. 如图，为估计池塘岸边A、B的距离，小方在池塘的一侧选取一点O，测得OA＝15米，OB=10米，A、B间的距离不可能是（ ）
A、20米 B、15米 C、10米 D、5米5. 如图，锐角△ABC的高AD、BE相交于F，若BF＝AC，BC＝7，CD＝2，则AF的长为 （ ）
A、2 B、3 C、4 D、56.在探索“尺规三等分角”这个数学名题的过程中，曾利用了如图，该图中，四边形ABCD是矩形，E是BA延长线上一点，F是CE上一点，∠ACF=∠AFC，∠FAE=∠FEA。若∠ACB=21°，则∠ECD的度数是（ ）
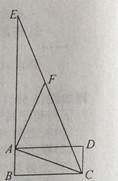A、7° B、21° C、23° D、24°7. 如图，AB∥CD，BE和CE分别平分∠ABC和∠BCD，AD过点E，且与AB互相垂直，点P为线段BC上一动点，连接PE．若AD＝8，则PE的最小值为（ ）
A、8 B、6 C、5 D、48. 如图，AD是△ABC的中线，E ， F分别是AD和AD延长线上的点，且DE＝DF ， 连接BF ， CE ， 下列说法：①CE＝BF；②△ABD和△ACD面积相等；③BF CE；④△BDF≌△CDE ． 其中正确的有（ ）
A、①②④ B、②③④ C、①②③ D、①②③④二、填空题
-
9. 在平面直角坐标系中，点（2021，﹣2021）关于x轴对称的点的坐标为 ．10. 如图所示，△ABC沿AB向下翻折得到△ABD，若∠ABC＝30°，∠ADB＝100°，则∠BAC的度数是 ．
11. 如图所示的方格中，∠1+∠2+∠3=度.
12. 如图，在△ABC中，D、E分别是BC、AD的中点，△ABC的面积为6cm2 ， 则△BDE的面积为 ．
13. 如图，AD=BC ， 要得到△ABD和△CDB全等，可以添加的条件是 ．
14. 我们规定：等腰三角形的顶角与一个底角度数的比值叫作等腰三角形的“特征值”，记作k．若 ，则该等腰三角形的顶角为度．15. 已知：如图， 是 的边 上的中线， ．中线 ．则 的取值范围是
16. 一个多边形切去一个角后，形成的另一个多边形的内角和为1 080°，那么原多边形的边数为.三、解答题
-
17. 如图，D是AB上一点，DF交AC于点E，DE=FE，FC∥AB，求证：
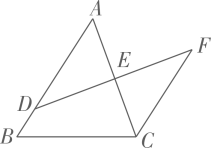18. 如图，已知∠ABC ， D是BC边上一点．求作一点P：
（ 1 ）使△PBD为等腰三角形且底边为BD ，
（ 2 ）点P到∠ABC两边的距离相等．（用尺规作图，保留痕迹，不写作法）
19. 如图所示，线段AC的垂直平分线交线段AB于点D ， ∠A=50°，
(1)、求证：△ADE≌△CDE ．(2)、求∠BDC度数．20. 如图，在边长为1个单位长度的小正方组成的网格中，按要求画出△A1B1C1与△A2B2C2.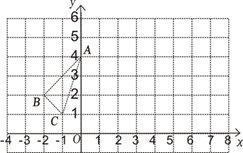
（ 1 ）作出△ABC关于y轴对称的△A1B1C1；
（ 2 ）将△ABC向右平移6个单位，作出平移后的△A2B2C2；
（ 3 ）观察△A1B1C1和△A2B2C2 ， 他们是否关于某直线对称？若是，请用粗线条画出对称轴.
21. 如图，在△ABC中，∠BAC=90°，AB=AC，直线MN经过点A，过点B作BD⊥MN于D，过C作CE⊥MN于E．
(1)、求证：△ABD≌△CAE；(2)、若BD=12cm，DE=20cm，求CE的长度．22. 如图，四边形ABCD中，∠B=90°， AB//CD，M为BC边上的一点，AM平分∠BAD，DM平分∠ADC，
求证：
(1)、AM⊥DM；(2)、M为BC的中点.23. 将纸片△ABC沿DE折叠使点A落在点 处
(1)、如图①，点A落在四边形BCDE的边BE上，则∠A与∠1之间的数量关系是；(2)、如图②，若点A落在四边形BCDE的内部，则∠A与∠1+∠2之间存在怎样的数量关系？并说明理由．(3)、如图③，点A落在四边形BCDE的外部，若∠1＝80°，∠2＝24°，求∠A的度数．24. 如图，已知△ABC中，∠B=∠C，AB=8厘米，BC=6厘米，点D为AB的中点．如果点P在线段BC上以每秒2厘米的速度由B点向C点运动，同时，点Q在线段CA上以每秒a厘米的速度由C点向A点运动，设运动时间为t（秒）（0<t<3）．
(1)、用含t的代数式表示PC的长度；(2)、若点P、Q的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；(3)、若点P、Q的运动速度不相等，当点Q的运动速度a为多少时，能够使△BPD与△CQP全等?