黑龙江省齐齐哈尔市龙沙区2021-2022学年八年级上学期期中数学试题
试卷更新日期：2021-12-01 类型：期中考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 已知三角形两边的长分别是3和7，则此三角形第三边的长可能是（ ）A、1 B、2 C、8 D、113. 若一个多边形的内角和等于其外角和的3倍，则这个多边形的边数是（ ）A、5 B、6 C、7 D、84. 计算（﹣ab）3•a2的结果是（ ）A、a5b3 B、a6b3 C、﹣a5b3 D、﹣a6b35. 如图，D是△ABC中BC边上一点，AB＝AC＝BD ， 则∠2＝24°则∠1＝（ ）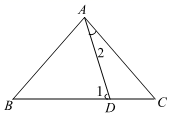
A、44° B、68° C、64° D、54°6. 在△ABC中，AB＝AC ， ∠B＝50°，P是边AB上的一个动点（不与顶点A重合），则∠BPC的值可能是（ ）
A、95° B、140° C、50° D、40°7. （2016福建省莆田市）如图，OP是∠AOB的平分线，点C ， D分别在角的两边OA ， OB上，添加下列条件，不能判定△POC≌△POD的选项是（ ）
A、PC⊥OA ， PD⊥OB B、OC=OD C、∠OPC=∠OPD D、PC=PD8. 下列语句中，正确的是（ ）A、等腰三角形底边上的中线就是底边上的垂直平分线 B、等腰三角形的对称轴是底边上的高 C、腰上的高也是中线的三角形是等边三角形 D、角可看作是以它的角平分线为对称轴的轴对称图形9. 如图，在∠AOB的两边上，分别取OM＝ON，再分别过点M、N作OA、OB的垂线，交点为P，画射线OP，则OP平分∠AOB的依据是 （填判定三角形全等方法的简称）（ ）
A、SSS B、SAS C、ASA D、HL10. 如图，在△ABC 中，∠ABC 的平分线交 AC 于点 D，AD＝6，过点 D 作 DE∥BC 交 AB 于点 E， 若△AED 的周长为 16，则边 AB 的长为（ ）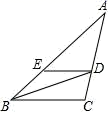
A、6 B、8 C、10 D、111. 如图，在△ACD和△BCE中，AC＝BC ， AD＝BE ， CD＝CE ， ∠ACE＝55°，∠BCD＝155°，AD与BE相交于点P ， 则∠BPD的度数为（ ）
A、110° B、125° C、130° D、155°12. 如图，已知∠MON＝30°，点A1、A2、A3…在射线N上，点B1、B2、B3……在射线OM上；△A1B1A2、△A2B2A3、△A3B3A4……均为等边三角形若OA1＝1，则△A2020B2020A2021的边长（ ）
A、22019 B、4040 C、4038 D、22020二、填空题
-
13. 已知如图，已知BD平分∠ADC ， 要使△ABD≌△CBD ， 还需添加一个条件，你添加的条件是 ． （只需写一个，不添加辅助线）
14. 如图，在△ABC中，∠ACB＝90°，将△ACD沿CD折叠，使点A恰好落在BC边上的点E处．若∠B＝26°，则∠BDE＝ ．
15. 计算：若a3n＝3，b2n＝2，则a6nb4n＝ ．16. 若实数m、n满足等式 ，且m、n恰好是等腰△ABC的两条边的边长，则△ABC的周长是 ．17. 如图，△ABC中，AB＝AC ， AB的垂直平分线交边AB于D点，交边AC于E点，若△ABC的周长是40cm，AB﹣BC＝8cm，则△BEC的周长是 cm．
18. 如图，已知OP平分∠AOB ， ∠AOB＝60°，PD⊥OA于点D ， PE⊥OB于点E ， PE＝2．如果点M是OP的中点，则DM的长是 ．
19. 如图，∠AOB=60°，OC平分∠AOB，如果射线OA上的点E满足△OCE是等腰三角形，那么∠OEC的度数为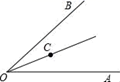
20. 如图，在△ABC中，∠BAC=90°，AD是高，BE是中线，CF是角平分线，CF交AD于点G，交BE于点H，下面说法中正确的序号是 ．①△ABE的面积等于△BCE的面积；②∠AFG=∠AGF；③∠FAG=2∠ACF；④BH=CH．
21. 如图，点P是∠AOB内任意一点，OP＝8cm，点M和点N分别是射线OA和射线OB上的动点，若PN+PM+MN的最小值是8cm，则∠AOB的度数是 ．
22. 如图，在 中，E为AC的中点，AD平分∠BAC，BA：CA＝2：3，AD与BE相交于点O，若 的面积比 的面积大1，则 的面积是.
三、解答题
-
23. 计算：(1)、b2•（﹣b）3•（﹣b2）4(2)、﹣（﹣2a2b3）4+（3a4b6）224. 如图，在直角坐标系中，先描出点A（1，3），点B（4，1）．
（ 1 ）描出点A关于x轴的对称点A1的位置，写出A1的坐标 ；
（ 2 ）在x轴上找一点C ， 使AC+BC的值最小，请描出C点的位置；
（ 3 ）用尺规在y轴上找一点P ， 使PA＝PB（保留作图痕迹）．
25. 如图，在△ABC中，AE平分∠BAC ， AD是BC边上的高．
(1)、在图中将图形按题意补充完整；(2)、当∠B＝28°，∠C＝72°时，求∠DAE的度数．26. 如图，已知等腰三角形ABC中，AB=AC，点D、E分别在边AB、AC上，且AD=AE，连接BE、CD，交于点F．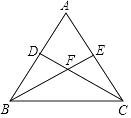
(1)、判断∠ABE与∠ACD的数量关系，并说明理由；(2)、求证：过点A、F的直线垂直平分线段BC．27. 如图，在△ABC中，AB＝AC ， 点D、E、F分别在AB、BC、AC边上，且BE＝CF ， BD＝CE ．
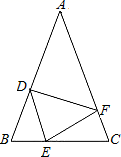(1)、求证：△DEF是等腰三角形；(2)、当∠A＝40°时，求∠DEF的度数．28. 已知如图，AD＝AB ， AC＝AE ， ∠ACB＝∠DAB＝90°，且AG⊥DG ， AE∥CB ， AC、DE交于点F ．
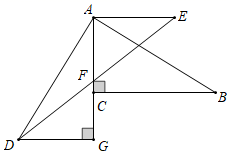(1)、求证：∠DAC＝∠B；(2)、求证：DG＝AE；(3)、猜想线段AF、BC的数量关系是 ， 请说明理由．29. 在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED＝EC ．
(1)、当点E为AB的中点时，如图1，确定线段A与DB的大小关系，请你直接写出结论：AEDB（填“＞”，“＜”或“＝”）．(2)、当E不是AB的中点时，AE与DB的大小关系是：AEDB（填“＞”，“＜”或“＝”）．理由如下：如图2，过点E作EF∥BC ， 交AC点F ． 请你接下来按照这种思路完成全部解答过程．(3)、在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED＝EC ． 若△ABC的边长为2，AE＝4，则CD的长为 ．