安徽省合肥市包河区2021-2022学年八年级上学期期中数学试题
试卷更新日期：2021-12-01 类型：期中考试
一、单选题
-
1. 平面直角坐标系中，点A（﹣2，1）到x轴的距离为（ ）A、﹣2 B、1 C、2 D、2. 若xy＞0，则关于点P（x，y）的说法正确的是（ ）A、在一或二象限 B、在一或四象限 C、在二或四象限 D、在一或三象限3. 一次函数y=2x+3的图像不经过的象限是（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 已知一次函数y=(m－1)x+1的图象上两点A（x1 ， y1）B（x2 ， y2），当x1>x2时，有y1<y2那么m的取值范围是（ ）A、m>0 B、m<0 C、m>1 D、m<15. 象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏.如图，是一局象棋残局，已知表示棋子“馬”和“車”的点的坐标分别为（4，3），（-2，1），则表示棋子“炮”的点的坐标为（ ）
A、 B、 C、 D、6. 在下列条件中，能确定 是直角三角形的条件有（ ）① ，② ，③ ，④
A、1个 B、2个 C、3个 D、4个7. 如图，在 ABC中，∠A＝30°，则∠1＋∠2的度数为（ ）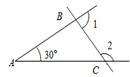
A、210° B、110° C、150° D、100°8. 如图，在平面直角坐标系xOy中，如果一个点的坐标可以用来表示关于x 、y的二元一次方程组 的解，那么这个点是（ ）
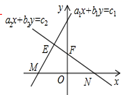A、M B、N C、E D、F9. 若 的三个内角 ， ， 满足关系式 ，则此三角形（ ）A、一定是直角三角形 B、一定是钝角三角形 C、一定有一个内角为45° D、一定有一个内角为60°10. 如图，点A(O，1)、点A1(2，0)、点A2(3，2)、点A3(5，1)、…，按照这样的规律下去，点A2021的坐标为 （ ）
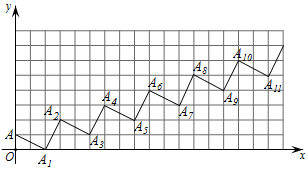A、(2022，2021) B、(3032，1010) C、(3033， 1011) D、(2021，1012)二、填空题
-
11. 点(2，3)关于y轴对称的点的坐标为 ．12. 已知点 在x轴上，则m等于.13. 三角形三边长分别为3，2a -1，8，则a的取值范围是 ．14. 如图，直线y＝kx+b（k、b是常数k≠0）与直线y＝2交于点A（4，2），则关于x的不等式kx+b＜2的解集为 ．
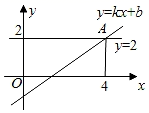15. 将直线y=2x-1向左平移，使其经过点(- ，0)，则平移后的直线所对应的函数关系式为 ．16. △ABC中，AE是角平分线，AD是边BC上的高，过点B做BF∥AE ， 交直线AD于点F ， ∠ABC=a ， ∠ACB=β ， 且a＞β ， 则∠AFB= (用a ， β表示)17. 如果不论k为何值，一次函数y= 的图象都经过一定点， 则该定点的坐标是 ．三、解答题
-
18. 在平面直角坐标系中，点M的坐标为(a ， 1－2a)．(1)、当a＝－1时，点M在坐标系的第象限(直接填写答案)；(2)、将点M向左平移2个单位，再向上平移1个单位后得到点N ， 当点N在第三象限时，求a的取值范围．19. 如图，点A、B、C都落在网格的顶点上．
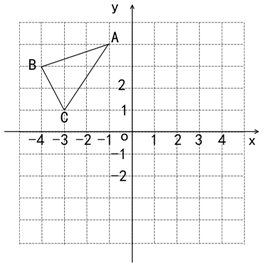(1)、写出点A、B、C的坐标；(2)、求△ABC的面积；(3)、把△ABC先向右平移4个单位长度，再向下平移5个单位长度，得△A´B´C´ ， 画出△A´B´C´20. 已知等腰△ABC ， 解答以下问题：(1)、若有一个内角为40°，求这个等腰三角形另外两个角的度数；(2)、若等腰三角形的周长为27，两条边长分别是a和2a+1，求三边的长21. 已知一次函数y1=(m-1)x+5-m ， y2=(n+1)x+1-n ．(1)、若y1的图象经过点(0，3)，求y1函数的解析式；(2)、若y2的图象经过第一、二、三象限，求n的取值范围；(3)、当m=n ， 且y1＜y2时，求x的取值范围．22. 某水产品商店销售1千克A种水产品的利润为10元，销售1千克B种水产品的利润为15元，该经销商决定一次购进A、B两种水产品共200千克用于销售，设购进A种水产品x千克，销售总利润为y元．(1)、求y与x之间的函数关系式；(2)、若其中B种水产品的进货量不超过A种水产品的3倍，请你帮该经销商设计一种进货方案使销售总利润最大，并求出总利润的最大值．23. 某天中午，小明从文具店步行返回学校，与此同时，小亮从学校骑自行车去文具店购买文具(购买文具时间忽略不计)，然后原路返回学校，两人均匀速行驶，结果两人同时到达学校．小明、小亮两人离书店的路程y1、y2(单位：米)与出发时间x(单位：分)之间的函数图象如图所示．
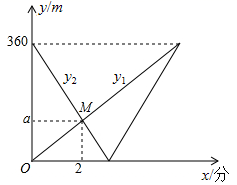(1)、学校和文具店之间的路程是米， 小亮的速度是小明速度的倍；(2)、求a的值，并解释图中点M的横坐标、纵坐标的实际意义；(3)、小明与小亮迎面相遇以后，再经过多长时间两人相距20米？