山西省太原市2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-12-01 类型：期中考试

进入出卷网下载

一、单选题

1. 一元二次方程x²＝3x的解是（）

A、x＝3 B、x＝﹣3 C、x₁＝3，x₂＝0 D、x₁＝﹣3，x₂＝0

查看试题解析
2. 菱形和矩形都具有的性质是（）

A、四条边相等 B、四个角相等 C、对角线互相垂直 D、对角线互相平分

查看试题解析
3. 在一个不透明的袋子里，装有6枚白色棋子和若干枚黑色棋子，这些棋子除颜色外都相同．将袋子里的棋子摇匀，随机摸出一枚棋子，记下它的颜色后再放回袋子里．不断重复这一过程，统计发现，摸到白色棋子的频率稳定在0.1，由此估计袋子里黑色棋子的个数为（）

A、60 B、56 C、54 D、52

查看试题解析
4. 已知关于x的一元二次方程2x²+3x+m﹣4＝0有一根是0，则m的值等于（）

A、4 B、±1 C、±4 D、﹣4

查看试题解析
5. 从1，2，3中任取一个数作为十位上的数字，从4，5中任取一个数作为个位上的数字，组成的两位数是偶数的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
6. 如图是一个活动的平行四边形ABCD框架，∠ABC＝40°，拉动两个不相邻的顶点B和D ，当边BA绕点B逆时针旋转α（0°＜α＜90°）时成为了矩形ABCD框架，则旋转角α的度数为（）

A、40° B、50° C、60° D、90°

查看试题解析
7. 方程2x²+3x﹣5＝0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
8. 某蔬菜种植基地2019年蔬菜产量为520吨，2021年蔬菜产量为1170吨．设该基地这两年蔬菜产量的年平均增长率为x ，根据题意列出的方程是（）

A、520（1+x）+520（1+x）²＝1170 B、520（1+x）²＝1170 C、520（1+2x）＝1170 D、520+520（1+x）+520（1+x）²＝1170

查看试题解析
9. 如图，在活动课上，老师画出边长为2的正方形ABCD ，让同学们按以下步骤完成画图：
⑴画出AD的中点E ，连接BE；

⑵以点E为圆心，EB长为半径画弧，交DA的延长线于点F；

⑶以AF为边画正方形AFGH ，点H在AB边上．在画出的图中有一条线段的长是方程x²+2x﹣4＝0的一个根．这条线段是（）

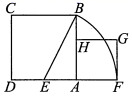A、线段BH B、线段BE C、线段AE D、线段AH

查看试题解析
10. 如图，BE和CD是 $△$ ABC的高，点G ， F分别是DE ， BC的中点，连接DF ， FE ， FG ．下列结论正确的是（）

A、DE＝FG B、DF＝EF C、DF⊥FE D、DF平分线段BE

查看试题解析
11. 如图，BE和CD是 $△$ ABC的高，点G ， F分别是DE ， BC的中点，连接DF ， FE ， FG ．若BC＝6，DE＝4，则FG的长为（）

A、3 B、 $\sqrt{5}$ C、2 D、 $\sqrt{3}$

查看试题解析

二、填空题

12. 写出一个四边形，使它既是中心对称图形又是轴对称图形，则这个四边形可能是．

查看试题解析

13. 小麦是中国重要的粮食作物之一，传入中国的时间较早据考古发掘新疆孔雀河流域新石器时代遗址出土的炭化小麦，距今400年以上．今年某乡村振兴实验室，从某小麦新品种的种子中抽取6批，在相同条件下进行发芽实验，数据统计如表：

种子粒数	100	400	800	1000	2000	5000
发芽种子粒数	95	358	744	893	1804	4505
发芽频率	0.950	0.895	0.930	0.893	0.902	0.901

据此可知，该种子发芽的概率为（精确到0.1）．

查看试题解析

14. 学校秋季运动会上，九年级准备队列表演，一开始排成8行12列，后来又有84名同学积极参加，使得队列增加的行数比增加的列数多1．现在队列表演时的列数是．

查看试题解析
15. 在探究一元二次方程x²+12x﹣15＝0的近似解时，小明所在的小组采用了赋值法，计算结果如表：

　x

1.1

1.2

1.3

1.4

x²+12x﹣15

-0.59

0.84

2.29

3.76

小组同学说，他们发现了该方程的一个近似解．这个近似解的十分位是．

查看试题解析
16. 如图，在平行四边形ABCD中，对角线AC与BD相交于点O ， △ABO是等边三角形，BC＝8．AE平分∠BAD交BC于点E ，连接OE ．请从A ， B两题中任选一题作答

(1)、线段AE的长等于．

(2)、线段OE的长等于．

查看试题解析

三、解答题

17. 解方程：

(1)、x²﹣3x﹣5＝0；

(2)、（x﹣2）²＝x﹣2．

查看试题解析
18. 如图，锐角 $△$ ABC中，AD平分∠BAC交BC于点D

(1)、尺规作图：作AD的垂直平分线交AB于点E ，交AC于点F ，连接DE ， DF；

(2)、证明（1）中的四边形AEDF是菱形．

查看试题解析

19. 阅读解关于x的一元二次方程ax²+bx+c＝0（a≠0）的过程，解答下列问题：

解：两边同乘以4a ，得4a²x²+4abx+4ac＝0．……第一步

移项，得4a²x²+4abx＝﹣4ac ． ……第二步

配方，得4a²x²+4abx+b²＝b²﹣4ac ． ……第三步

（2ax+b）²＝b²﹣4ac ． ……第四步

两边开平方，得 $2 a x + b = \pm \sqrt{b^{2} - 4 a c}$ ……第五步

$2 a x = - b \pm \sqrt{b^{2} - 4 a c}$ ．……第六步

所以， $x_{1} = \frac{- b + \sqrt{b^{2} - 4 a c}}{2 a} ， x_{2} = \frac{- b - \sqrt{b^{2} - 4 a c}}{2 a}$ ．……第七步

(1)、第一步变形的依据是；

(2)、从第步开始出现错误，错误的原因是；

(3)、采用上述解方程的思路，求3x²﹣4x﹣2＝0的根．

查看试题解析

20. 2021年8月5日，全红婵连获三跳满分以总分466.2分打破世界纪录，夺得2020东京奥运会跳水女子单人10米跳台金牌，令世界为之瞩目．训练中，教练要求她在距水面5m前完成规定的翻腾动作，教练组经过长期数据分析，得出她起跳后的运动时间t（s）和距离水面的高度h（m）之间的关系式基本满足h＝10 $+ \frac{5}{2}$ t﹣5t² ．求她最多用多长时间完成规定动作．

查看试题解析
21. 小明、小亮和小颖三人做“石头、剪刀和布”的游戏．小颖说：你俩玩，我裁判，并制定了如下的游戏规则：如果你俩的手势相同，我获胜；如果你俩的手势不同，按“石头胜剪刀，剪刀胜布，布胜石头”的规则决定获胜者．假设小明与小亮每次出这三种手势的可能性相同，通过列表或画树状图的方法，分析这个游戏规则是否公平．

查看试题解析
22. 如图，在菱形ABCD中，点E ， F是对角线BD的三等分点，连接AE ， EC ， CF和FA ．已知AB＝2 $\sqrt{10}$ ，四边形AECF是正方形，求BD的长．

查看试题解析
23. 今年是中国共产党建党100周年，中华人民共和国成立72周年！在国庆前夕，社区便民超市调查了某种水果的销售情况获得如下信息：
信息一：进价是每千克12元；

信息二：当销售价为每千克27元时，每天可售出120千克；

若每千克售价每降低2元，则每天的销售量将增加80千克．根据以上信息解答问题：该超市每天想要获得3080元的销售利润，又要尽可能让顾客得到实惠，求这种水果的销售单价应为多少元．

查看试题解析
24. 综合与实践
折叠操作

操作1：如图1，矩形纸片ABCD的边AB＝10cm，将纸片沿MN折叠使得BC与AD重合，得到图2；

操作2：沿过点M的直线折叠，使得点A落在MN上；沿过点N的直线折叠，使得点D落在MN上，两条折痕交于点E ，得到图3；

操作3：把所有折叠部分展开铺平，折痕的交点分别为点E ，点E'，ME交AD于点F ，得到图4．

问题探究

(1)、判断四边形MENE'的形状，并说明理由；

(2)、请从AB两题中任选一题作答．
A ．若EN＝ND ，求AD的长．

B ．连接AE ，若 $△$ AME是等腰三角形，求AD的长．

查看试题解析

x	1.1	1.2	1.3	1.4
x²+12x﹣15	-0.59	0.84	2.29	3.76