山东省烟台市芝罘区(五四制)2021-2022学年九年级上学期期中考试数学试题
试卷更新日期:2021-12-01 类型:期中考试
一、单选题
-
1. 在Rt△ABC中,∠C=90°,cosA= ,则sinA的值是( )A、 B、 C、 D、2. 若抛物线y=x2+bx+c的对称轴为y轴,且点P(2,6)在该抛物线上,则c的值为( )A、﹣2 B、0 C、2 D、43. 已知抛物线 上部分点的横坐标x 与纵坐标y的对应值如表:
…
1
2
3
4
5
…
…
-5
…
根据如表,下列判断正确的是 ( )
A、该抛物线开口向上 B、该抛物线的对称轴是直线x=1 C、该抛物线一定经过点 D、该抛物线在对称轴左侧部分y随x的增大而减小4. 二次函数y=x2+4x+3的图象可以由二次函数y=x2的图象平移而得到,下列平移正确的是( )A、先向左平移2个单位,再向上平移1个单位 B、先向左平移2个单位,再向下平移1个单位 C、先向右平移2个单位,再向上平移1个单位 D、先向右平移2个单位,再向下平移1个单位5. 如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )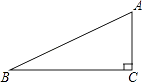 A、
A、 B、
B、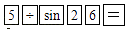 C、
C、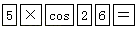 D、
D、 6. 如图,一块矩形木板ABCD斜靠在墙边,( OC⊥OB , 点A、B、C、D、O在同一平面内),已知AB=a , AD=b , ∠BCO=α . 则点A到OC的距离等于( )
6. 如图,一块矩形木板ABCD斜靠在墙边,( OC⊥OB , 点A、B、C、D、O在同一平面内),已知AB=a , AD=b , ∠BCO=α . 则点A到OC的距离等于( ) A、asinα+bsinα B、acosα+bcosα C、asinα+bcosα D、acosα+bsinα7. 若点A(﹣4,y1),B(﹣1,y2),C(1,y3)都是二次函数y=x2+4x+k的图象上的点,则( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y2<y1 D、y3<y1<y28. 如图,在Rt△ABC中,∠BAC=90°,过A作AD⊥BC于点D , 若 = .则tanC的值为( )
A、asinα+bsinα B、acosα+bcosα C、asinα+bcosα D、acosα+bsinα7. 若点A(﹣4,y1),B(﹣1,y2),C(1,y3)都是二次函数y=x2+4x+k的图象上的点,则( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y2<y1 D、y3<y1<y28. 如图,在Rt△ABC中,∠BAC=90°,过A作AD⊥BC于点D , 若 = .则tanC的值为( ) A、 B、 C、 D、9. 已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )A、
A、 B、 C、 D、9. 已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )A、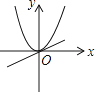 B、
B、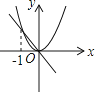 C、
C、 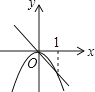 D、
D、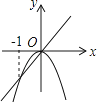 10. 如图, 的顶点都在边长相等的小正方形的顶点上,则 等于( )
10. 如图, 的顶点都在边长相等的小正方形的顶点上,则 等于( ) A、 B、 C、 D、11. 如图,已知二次函数 图象的对称轴为直线 ,下列结论:( )
A、 B、 C、 D、11. 如图,已知二次函数 图象的对称轴为直线 ,下列结论:( )
① ;
② ;
③ ;
④若图象经过点(-3,-2),方程 的两根为 , ,则 .其中正确的结论的个数是( )
A、4个 B、3个 C、2个 D、1个12. 如图,矩形纸片ABCD中,BC=4,AB=3,点P是BC边上的动点(点P不与点B、C重合).现将△PCD沿PD翻折,得到△PC′D , 作∠BPC′的角平分线,交AB于点E . 设BP=x , BE=y , 则下列图象中,能表示y与x的函数关系的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 二次函数 的图象经过原点,则 .14. 如图,在 中, , , 的垂直平分线 交 于 ,连接 .若 ,则 .
 15. 已知抛物线 的顶点在坐标轴上,则 .16. 如图甲、乙两艘船同时从港口 A 出发,甲船沿北偏东45°的方向前进,乙船沿北偏东75°方向以每小时30海里的速度前进,两船航行两小时分别到达B , C处,此时测得甲船在乙船的正西方向,则此时甲、乙两船之间的距离是海里.
15. 已知抛物线 的顶点在坐标轴上,则 .16. 如图甲、乙两艘船同时从港口 A 出发,甲船沿北偏东45°的方向前进,乙船沿北偏东75°方向以每小时30海里的速度前进,两船航行两小时分别到达B , C处,此时测得甲船在乙船的正西方向,则此时甲、乙两船之间的距离是海里. 17. 已知二次函数y= x²+2若自变量x的取值范围是-1≤x≤2,则函数y的取值范围是 .18. 如图,平面直角坐标系中,点A、B坐标分别为(3,0)、(0,4),点C是x轴正半轴上一点,连接BC . 过点A垂直于AB的直线与过点C垂直于BC的直线交于点D , 连接BD , 则sin∠BDC的值是 .
17. 已知二次函数y= x²+2若自变量x的取值范围是-1≤x≤2,则函数y的取值范围是 .18. 如图,平面直角坐标系中,点A、B坐标分别为(3,0)、(0,4),点C是x轴正半轴上一点,连接BC . 过点A垂直于AB的直线与过点C垂直于BC的直线交于点D , 连接BD , 则sin∠BDC的值是 .
三、解答题
-
19. 计算:(sin30°﹣1)0﹣ sin45°+tan60°cos30°20. 在体育测试时,初三的一名高个子男同学推铅球,已知铅球所经过的路线是某个二次函数图象的一部分,如图所示,如果这个男同学的出手处 点的坐标 ,铅球路线的最高处 点的坐标为 (单位:米)
 (1)、求这个二次函数的解析式;(2)、该男同学把铅球推出去多远?21. 如图,在平面直角坐标系中,OB=5,sin∠AOB= ,点A的坐标为(10,0).
(1)、求这个二次函数的解析式;(2)、该男同学把铅球推出去多远?21. 如图,在平面直角坐标系中,OB=5,sin∠AOB= ,点A的坐标为(10,0).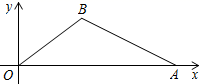 (1)、求点B 的坐标;(2)、求sin∠OAB的值.22. 如图,有长为21m的篱笆,一面利用墙(墙的最大可用长度为10m)围成中间隔有一道篱笆的长方形养鸡场,设养鸡场的宽 为x m,面积为 .
(1)、求点B 的坐标;(2)、求sin∠OAB的值.22. 如图,有长为21m的篱笆,一面利用墙(墙的最大可用长度为10m)围成中间隔有一道篱笆的长方形养鸡场,设养鸡场的宽 为x m,面积为 . (1)、y与x的函数关系为 , 其中x的取值范围为 , 函数图象的对称轴为;(2)、当养鸡场的面积为 时,求养鸡场的宽;(3)、求养鸡场面积的最大值.23. 某校为了更好的记录学生们在秋季运动会中精彩的瞬间,学校特意邀请了一名摄影师携带无人机来进行航拍.如图,摄影师在水平地面上点A测得无人机位置点C的仰角为53°;当摄影师迎着坡度为1:2.4的斜坡从点A走到点B时,无人机的位置恰好从点C水平飞到点D , 此时,摄影师在点B测得点D的仰角为45°,其中AB=2.6米,CD=3米,无人机与水平地面之间的距离始终保持不变,且A、B、C、D四点在同一平面内,求无人机距水平地面的高度.(参考数据: , , )
(1)、y与x的函数关系为 , 其中x的取值范围为 , 函数图象的对称轴为;(2)、当养鸡场的面积为 时,求养鸡场的宽;(3)、求养鸡场面积的最大值.23. 某校为了更好的记录学生们在秋季运动会中精彩的瞬间,学校特意邀请了一名摄影师携带无人机来进行航拍.如图,摄影师在水平地面上点A测得无人机位置点C的仰角为53°;当摄影师迎着坡度为1:2.4的斜坡从点A走到点B时,无人机的位置恰好从点C水平飞到点D , 此时,摄影师在点B测得点D的仰角为45°,其中AB=2.6米,CD=3米,无人机与水平地面之间的距离始终保持不变,且A、B、C、D四点在同一平面内,求无人机距水平地面的高度.(参考数据: , , ) 24. 某品牌钢笔进价为每支20元,经销商小周在销售中发现,每月销售量y(支)与销售单价x(元)之间满足一次函数y=﹣10x+500的关系,在销售中销售单价不低于进价,而每支钢笔的利润不高于进价的60%,设小周每月获得利润为w(元).(1)、当销售单价定为每支多少元时,每月可获得最大利润?每月的最大利润是多少?(2)、如果小周想要每月获得的利润不低于2000元,那么小周每月的成本最少需要多少元?(成本=进价×销售量).25. 如图①,在平面直角坐标系中,抛物线 ( )与x轴交于点A、B , 与y轴交于点C , 且OA=2,OB=OC=6.
24. 某品牌钢笔进价为每支20元,经销商小周在销售中发现,每月销售量y(支)与销售单价x(元)之间满足一次函数y=﹣10x+500的关系,在销售中销售单价不低于进价,而每支钢笔的利润不高于进价的60%,设小周每月获得利润为w(元).(1)、当销售单价定为每支多少元时,每月可获得最大利润?每月的最大利润是多少?(2)、如果小周想要每月获得的利润不低于2000元,那么小周每月的成本最少需要多少元?(成本=进价×销售量).25. 如图①,在平面直角坐标系中,抛物线 ( )与x轴交于点A、B , 与y轴交于点C , 且OA=2,OB=OC=6. (1)、求抛物线的解析式;(2)、点D是第一象限内抛物线上的动点,连接OD交BC于点E , 求 的最大值,并求出此时点D的坐标;(3)、如图②,点P是抛物线对称轴l上一点,是否存在点P的位置,使△BCP是直角三角形?若存在,请直接写出相应点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点D是第一象限内抛物线上的动点,连接OD交BC于点E , 求 的最大值,并求出此时点D的坐标;(3)、如图②,点P是抛物线对称轴l上一点,是否存在点P的位置,使△BCP是直角三角形?若存在,请直接写出相应点P的坐标;若不存在,请说明理由.