山东省烟台市栖霞市2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-12-01 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各问题中，两个变量之间的关系不是反比例函数的是

A、小明完成100m赛跑时，时间t（s）与跑步的平均速度v（m/s）之间的关系. B、菱形的面积为48cm² ，它的两条对角线的长为y（cm）与x（cm）的关系. C、一个玻璃容器的体积为30L时，所盛液体的质量m与所盛液体的体积V之间的关系. D、压力为600N时，压强p与受力面积S之间的关系.

查看试题解析
2. 已知，一个小球由桌面沿着斜坡向上前进了 $10 cm$ ，此时小球距离桌面的高度为 $5 cm$ ，则这个斜坡的坡度 $i$ 为（）

A、 $2 ： 1$ B、 $1 ： 2$ C、 $1 ： \sqrt{2}$ D、 $1 ： \sqrt{3}$

查看试题解析
3. 若函数 $y = (3 - 2 m) x^{m^{2} - 7} - x + 1$ 是二次函数，则m的值为（）

A、3 B、-3 C、 $\pm 3$ D、9

查看试题解析
4. 已知反比例函数 $y = - \frac{2}{x}$ ，则下列结论正确的是（）

A、点(1，2)在它的图象上 B、其图象分别位于第一、三象限 C、 $y$ 随 $x$ 的增大而减小 D、如果点 $P (m, n)$ 在它的图象上，则点 $Q (n, m)$ 也在它的图象上

查看试题解析
5. 在 $△ A B C$ 中，(2sinA-1)²+ $\sqrt{\cos B - \frac{1}{2}}$ =0，则 $△ A B C$ 是（）

A、等边三角形 B、等腰三角形 C、直角三角形 D、无法确定

查看试题解析
6. 已知二次函数 $y = x^{2} + 2 x + 4$ ，下列说法正确的是（）

A、抛物线开口向下 B、当 $x > 3$ 时， $y$ 随 $x$ 的增大而减小 C、二次函数的最小值是2 D、抛物线的对称轴是直线 $x = - 1$

查看试题解析
7. 函数 $y = a x$ 与 $y = \frac{b}{x} (a b \neq 0)$ 的图象的两个交点的坐标分别为 $(3 ， m)$ ， $(n ， - 2)$ ，则 $m$ ， $n$ 的值分别是（）

A、2，﹣3 B、﹣2，﹣3 C、﹣2，3 D、2，3

查看试题解析
8. 如图，在△ABC中，sinB= $\frac{1}{3}$ ， tanC=2，AB=3，则AC的长为（）

A、 $\sqrt{2}$ B、 $\frac{\sqrt{5}}{2}$ C、 $\sqrt{5}$ D、2

查看试题解析
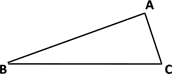9. 如图，小明以抛物线y=x²-2x+4为灵感设计了一款杯子，若AB=4，DE=2，则杯子的高CE为（）

A、4 B、5 C、6 D、7

查看试题解析
10. 如图，在平面直角坐标系中，反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象上有A、B两点，它们的横坐标分别为2和4， $△ A B O$ 的面积为6，则 $k$ 的值为（）

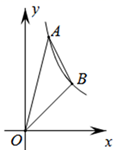A、4 B、8 C、10 D、12

查看试题解析
11. 如图，是直立在高速公路边水平地面上的交通警示牌，经测量得到如下数据：AM=4米，AB=8米，∠MAD=45°，∠MBC=30°，则警示牌的高CD为（）

A、4 $\sqrt{3}$ 米 B、（2 $\sqrt{3}$ +2）米 C、（4 $\sqrt{2}$ ﹣4）米 D、（4 $\sqrt{3}$ ﹣4）米

查看试题解析
12. 对称轴为直线x＝1的抛物线 $y = a x^{2} + b x + c$ （a、b、c为常数，且a≠0）如图所示，小明同学得出了以下结论：①abc＜0，②b²＞4ac，③4a＋2b＋c＞0，④3a＋c＞0，⑤a＋b≤m(am＋b)（m为任意实数）， ⑥当x＜－1时，y随x的增大而增大，其中结论正确的个数为（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

13. 如图，B(2，﹣2)，C(3，0)，以OC，CB为边作平行四边形OABC，则经过点A的反比例函数的解析式为．

查看试题解析
14. 计算： $2 \sin^{2} 45 ° + \tan 60 ° \cdot \tan 30 ° - \cos 60 ° =$ ．

查看试题解析
15. 若点M是反比例函数 $y = \frac{k}{x} (k \neq 0)$ 图象上任意一点， $M N ⊥ y$ 轴于 $N$ ，点 $p$ 在 $x$ 轴上， $Δ M N P$ 的面积为 $2$ ，则 $k$ 的值为
．

查看试题解析
16. 如图，若被击打的小球飞行高度 $h$ （单位： $m$ ）与飞行时间 $t$ （单位： $s$ ）之间具有的关系为 $h = 20 t - 5 t^{2}$ ，则小球从飞出到落地所用的时间为 $s$ ．

查看试题解析
17. 如图， $Δ A B C$ 的顶点都在边长相等的小正方形的顶点上，则 $\cos ∠ B A C$ 等于．

查看试题解析

三、解答题

18. 泡茶需要将电热水壶中的水先烧到100℃，然后停止烧水，等水温降低到适合的温度时再泡茶，烧水时水温y(℃)与时间x(min)成一次函数关系；停止加热过了1分钟后，水壶中水的温度y(℃)与时间x(min)近似于反比例函数关系(如图)．已知水壶中水的初始温度是20℃，降温过程中水温不低于20℃．

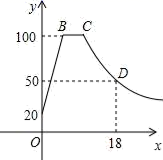(1)、分别求出图中所对应的函数关系式，并且写出自变量x的取值范围：

(2)、从水壶中的水烧开(100℃)降到90℃就可以泡茶，问从水烧开到泡茶需要等待多长时间？

查看试题解析
19. 如图，一轮船在海上以每小时 $30$ 海里的速度向西方向航行，上午 $8$ 时，在 $B$ 处测得小岛 $A$ 在北偏东 $30^{\circ}$ 方向，之后轮船继续向正西方向航行，于上午 $9$ 时到达 $C$ 处，这时测得小岛 $A$ 在北偏东 $60^{\circ}$ 方向．如果轮船仍继续向正西方向航行，于上午 $11$ 时到达 $D$ 处，这时轮船与小岛 $A$ 相距多远？

查看试题解析
20. 新冠肺炎疫情期间，某药店进了一批口罩，每包进价10元，每包销售价定为25元时，每天销售1000包．经一段时间调查，发现每包销售单价每上涨1元，每天就少卖40包．其销售单价不低于进价，销售利润率不高于180% ．设每包销售价为x元（x为正整数）．

(1)、请直接写出 $x$ 的取值范围．

(2)、设每天的总利润为 $w$ 元，当每包销售价定为多少元时，该药店每天的利润最大？最大利润是多少元？

查看试题解析
21. 如图，一次函数 $y = - x + 3$ 的图像与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 在第一象限的图像交于 $A (1 ， a)$ 和B两点，与x轴交于点C ．

(1)、求反比例函数的解析式；

(2)、求出另一个交点B的坐标，并直接写出当 $x > 0$ 时，不等式 $- x + 3 < \frac{k}{x}$ 的解集；

(3)、若点P在x轴上，且 $△ A P C$ 的面积为5，求点P的坐标．

查看试题解析
22. 如图，已知抛物线 $y = a x^{2} + b x + c$ 是由 $y = x^{2}$ 平移得到的，且经过 $A (1 ， 0)$ ， $B (0 ， 2)$ 两点，顶点为点 $M$ ．

(1)、求抛物线的解析式并求出点 $M$ 的坐标；

(2)、将 $Δ O A B$ 绕点 $A$ 顺时针旋转 $90 °$ 后，点 $B$ 落在点 $C$ 的位置，将抛物线沿 $y$ 轴平移后经过点 $C$ ，求平移后所得图象的函数关系式．

查看试题解析
23. 如图1是一种手机平板支架，由托板、支撑板和底座构成，手机放置在托板上，图2是其侧面结构示意图．量得托板长AB＝130mm，支撑板长CD＝80mm，底座长DE＝90mm．托板AB固定在支撑板顶端点C处，且CB＝40mm，托板AB可绕点C转动，支撑板CD可绕点D转动．（结果保留小数点后一位）

(1)、若∠DCB＝80°，∠CDE＝60°，求点A到直线DE的距离；

(2)、为了观看舒适，在（1）的情况下，把AB绕点C逆时针旋转10°后，再将CD绕点D顺时针旋转，使点B落在直线DE上即可，求CD旋转的角度．（参考数据：sin40°≈0.643，cos40°≈0.766，tan40°≈0.839，sin26.6°≈0.448，cos26.6°≈0.894，tan26.6°≈0.500， $\sqrt{3}$ ≈1.732）

查看试题解析
24. 如图，在平面直角坐标系中，二次函数y＝x²+bx+c的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，﹣3）点，点P是直线BC下方的抛物线上一动点．

(1)、求这个二次函数的解析式；

(2)、当点P运动到什么位置时，四边形ABPC的面积最大，求出此时P点的坐标和四边形ABPC的最大面积．

查看试题解析