山东省临沂市蒙阴县2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-12-01 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 抛物线 $y = - \frac{1}{2} {(x + 1)}^{2} - 2$ 的顶点坐标是（）

A、 $(- 1 ， - 2)$ B、 $(- 1 ， 2)$ C、 $(1 ， - 2)$ D、 $(1 ， 2)$

查看试题解析
3. 将一元二次方程 $x (x + 4) = 8 x + 12$ 化为一般形式，正确的是（）

A、 $x^{2} + 4 x + 12 = 0$ B、 $x^{2} + 4 x - 12 = 0$ C、 $x^{2} - 4 x - 12 = 0$ D、 $x^{2} - 4 x + 12 = 0$

查看试题解析
4. 方程 2x ² - x + 1 = 0的根的情况是（）

A、有一个实数根 B、有两个不相等的实数根 C、没有实数根 D、有两个相等的实数根

查看试题解析
5. 如图，PA是⊙O的切线，A为切点，PO的延长线交⊙O于点B ，若∠B＝32°，则∠P的度数为（）

A、24º B、26º C、28º D、32º

查看试题解析
6. 如图， $△ A B C$ 内接于⊙ $O$ ， $∠ B A C = 30 °$ ， $B C = 8$ ，则⊙ $O$ 半径为（）

A、4 B、6 C、8 D、12

查看试题解析
7. 如图，在Rt $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A B C = 30 °$ ，将 $△ A B C$ 绕点 $C$ 顺时针旋转 $α$ 角 $(0 ° < α < 180 °)$ 至 $△ A^{'} B^{'} C$ ，使得点 $A^{'}$ 恰好落在 $A B$ 边上，则 $α$ 等于（）

A、 $150 °$ B、 $90 °$ C、 $30 °$ D、 $60 °$

查看试题解析
8. 抛物线 $y = a x^{2} + b x + c$ 经过点 $A (- 3 ， 0)$ ，对称轴是直线 $x = - 1$ ，则 $a + b + c =$ （）

A、6 B、8 C、9 D、0

查看试题解析
9. 将抛物线 $y = x^{2} - 6 x + 5$ 向上平移两个单位长度，再向右平移一个单位长度后，得到的抛物线解析式是（）

A、 $y = {(x - 4)}^{2} - 6$ B、 $y = {(x - 1)}^{2} - 3$ C、 $y = {(x - 2)}^{2} - 2$ D、 $y = {(x - 4)}^{2} - 2$

查看试题解析
10. 一元二次方程 $x^{2} - 6 x - 6 = 0$ 配方后化为（）

A、 ${(x - 3)}^{2} = 15$ B、 ${(x - 3)}^{2} = 3$ C、 ${(x + 3)}^{2} = 15$ D、 ${(x + 3)}^{2} = 3$

查看试题解析
11. 铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式为y＝－ $\frac{1}{12}$ x²＋ $\frac{2}{3}$ x＋ $\frac{5}{3}$ .则该运动员此次掷铅球的成绩是(　　)

A、6 m B、12 m C、8 m D、10 m

查看试题解析
12. 目前以5G等为代表的战略性新兴产业蓬勃发展．某市2019年底有5G用户2万户，计划到2021年底全市5G用户数达到9.68万户．设全市5G用户数年平均增长率为x ，则x值为（　　）

A、120% B、130% C、140% D、150%

查看试题解析
13. 二次函数y＝-x²+（6-m）x+8，当x＞-2时，y随x的增大而减小；当x＜-2时，y随x的增大而增大，则m的值为（　　）

A、10 B、8 C、6 D、4

查看试题解析
14. 对称轴为直线x＝1的抛物线 $y = a x^{2} + b x + c$ （a、b、c为常数，且a≠0）如图所示，小明同学得出了以下结论：①abc＜0，②b²＞4ac，③4a＋2b＋c＞0，④3a＋c＞0，⑤a＋b≤m(am＋b)（m为任意实数）， ⑥当x＜－1时，y随x的增大而增大，其中结论正确的个数为（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

15. 已知 $x = 1$ 是方程 $x^{2} + b x - 2 = 0$ 的一个根，则方程的另一个根是．

查看试题解析
16. 已知关于x的一元二次方程（m﹣1）x²+2x+1＝0有实数根，则m的取值范围是．

查看试题解析
17. 在平面直角坐标系中，点A的坐标为 $(a ， - 3)$ ，点B的坐标是 $(4 ， b)$ ，若点A与点B关于原点O对称，则 $a b =$ ．

查看试题解析
18. 若二次函数 $y = x^{2} - 6 x + c$ 的图象过 $A (- 1 ， y_{1})$ ， $B (2 ， y_{2})$ ， $C (5 ， y_{3})$ ，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是．

查看试题解析
19. 已知抛物线 $y = x^{2} + b x + c$ 的部分图象如图所示，当 $y < 0$ 时， $x$ 的取值范围是．

查看试题解析

三、解答题

20. 解方程：

(1)、 $x^{2} + 4 x + 1 = 0$ ；

(2)、 $x^{2} - 10 x + 9 = 0$ ；

查看试题解析
21. 如图，在边长为1的正方形组成的网格中建立直角坐标系， $△ A O B$ 的顶点均在格点上，点O为原点，点A ， B的坐标分别是 $A (3 ， 2)$ 、 $B (1 ， 3)$ ．

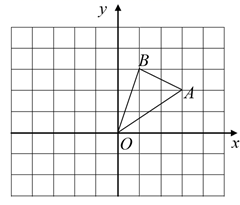(1)、将 $△ A O B$ 向下平移3个单位后得到 $△ A_{1} O_{1} B_{1}$ ，则点 $B_{1}$ 的坐标为；

(2)、将 $△ A O B$ 绕点O逆时针旋转90°后得到 $△ A_{2} O B_{2}$ ，请在图中作出 $△ A_{2} O B_{2}$ ，并求出这时点 $A_{2}$ 的坐标为；

(3)、在（2）中的旋转过程中，求出线段 $O A$ 扫过的图形的弧长．

查看试题解析
22. 某水果超市以每千克20元的价格购进一批樱桃，规定每千克樱桃售价不低于进价又不高于40元，经市场调查发现，樱桃的日销售量y（千克）与每千克售价x（元）满足一次函数关系 $y = - 2 x + 160$ ，

(1)、该超市要想获得1000元的日销售利润，每千克樱桃的售价应定为多少元？

(2)、当每千克樱桃的售价定为多少元时，日销售利润最大？最大利润是多少？

查看试题解析
23. 如图，在 $△ A B C$ 中， $A C = B C$ ， $∠ A C B = 120 °$ ， $A C$ 的垂直平分线 $M N$ 交 $A B$ 于点O ，以O为圆心， $O A$ 为半径作 $⊙ O$ ．

(1)、求证： $B C$ 是 $⊙ O$ 的切线；

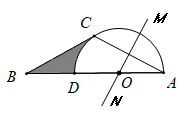(2)、若 $⊙ O$ 的半径为6，求图中阴影部分的面积．

查看试题解析
24.

(1)、如图①，在 $R t △ A B C$ 中， $A B = A C$ ， $D$ 为 $B C$ 边上一点(不与点 $B$ ， $C$ 重合)，将线段 $A D$ 绕点 $A$ 逆时针旋转90°得到 $A E$ ，连接 $E C$ ，试探索线段 $B C$ ， $D C$ ， $E C$ 之间满足的等量关系，并证明你的结论．

(2)、如图②，在 $R t △ A B C$ 与 $R t △ A D E$ 中， $A B = A C$ ， $A D = A E$ ，将 $△ A D E$ 绕点 $A$ 旋转，使点 $D$ 落在 $B C$ 边上，试探索线段 $A D$ ， $B D$ ， $C D$ 之间满足的等量关系，并证明你的结论．

查看试题解析
25. 如图，抛物线 $y = a x^{2} + b x + 8 (a \neq 0)$ 与x轴交于点 $A (- 2 ， 0)$ 和点 $B (8 ， 0)$ ，与y轴交于点C ，顶点为D ，连接 $A C$ ， $B C$ ．

(1)、求抛物线的表达式；

(2)、点E是抛物线的对称轴上一点，使得 $A E + C E$ 最短，求点E的坐标；

(3)、点P是第一象限内抛物线上的动点，连接 $P B$ ， $P C$ ．当 $S_{△ P B C}$ 最大时，求点P的坐标．

查看试题解析