山东省临沂市罗庄区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-12-01 类型:期中考试
一、单选题
-
1. 下列银行标志中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 方程 的根是( )A、 B、 C、 D、3. 如图,将△ABC绕点C顺时针旋转90°得到△EDC , 若点A、D、E在同一条直线上,∠ACB=25°,在∠ADC的度数是( )
2. 方程 的根是( )A、 B、 C、 D、3. 如图,将△ABC绕点C顺时针旋转90°得到△EDC , 若点A、D、E在同一条直线上,∠ACB=25°,在∠ADC的度数是( ) A、45° B、60° C、70° D、75°4. 抛物线 的对称轴是( )A、x= B、x=3 C、x=-3 D、x=65. 如图, 的内切圆 与 分别相切于点D , E , F , 连接 , , , , ,则阴影部分的面积为( )
A、45° B、60° C、70° D、75°4. 抛物线 的对称轴是( )A、x= B、x=3 C、x=-3 D、x=65. 如图, 的内切圆 与 分别相切于点D , E , F , 连接 , , , , ,则阴影部分的面积为( ) A、 B、 C、 D、6. 若实数x满足方程 ,那么 的值为( )A、-2或4 B、2或-4 C、-2 D、47. 如图,先将该图沿着它自己的右边缘翻折,再绕着右下角的一个端点按顺时针方向旋转 ,之后所得到的图形是( )
A、 B、 C、 D、6. 若实数x满足方程 ,那么 的值为( )A、-2或4 B、2或-4 C、-2 D、47. 如图,先将该图沿着它自己的右边缘翻折,再绕着右下角的一个端点按顺时针方向旋转 ,之后所得到的图形是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 在同一直角坐标系中,一次函数y=﹣kx+1与二次函数y=x2+k的大致图象可以是( )A、
8. 在同一直角坐标系中,一次函数y=﹣kx+1与二次函数y=x2+k的大致图象可以是( )A、 B、
B、 C、
C、 D、
D、 9. 若二次函数y=ax2+bx+c(a<0)的图象,过不同的五点A(-2,n)、B(6,n)、C(0,y1)、 D( ,y2)、E(3,y3),则y1、y2、y3的大小关系是( )A、 B、 C、 D、10. 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1 , 它与x轴交于点O , A1;将C1绕点A1旋转180°得C2 , 交x轴于点A2;将C2绕点A2旋转180°得C3 , 交x轴于点A3;…如此进行下去,直至得C5 . 若P(14,m)在第5段抛物线C5上,则m值为( )
9. 若二次函数y=ax2+bx+c(a<0)的图象,过不同的五点A(-2,n)、B(6,n)、C(0,y1)、 D( ,y2)、E(3,y3),则y1、y2、y3的大小关系是( )A、 B、 C、 D、10. 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1 , 它与x轴交于点O , A1;将C1绕点A1旋转180°得C2 , 交x轴于点A2;将C2绕点A2旋转180°得C3 , 交x轴于点A3;…如此进行下去,直至得C5 . 若P(14,m)在第5段抛物线C5上,则m值为( ) A、2 B、1.5 C、-2 D、-2.2511. 以半径为4的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( ).A、 B、 C、 D、12. 抛物线 的对称轴是直线 ,其图象如图所示.下列结论:① ;② ;③若 和 是抛物线上的两点,则当 时, ;④抛物线的顶点坐标为 ,则关于 的方程 无实数根.其中正确结论的个数是( )
A、2 B、1.5 C、-2 D、-2.2511. 以半径为4的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( ).A、 B、 C、 D、12. 抛物线 的对称轴是直线 ,其图象如图所示.下列结论:① ;② ;③若 和 是抛物线上的两点,则当 时, ;④抛物线的顶点坐标为 ,则关于 的方程 无实数根.其中正确结论的个数是( ) A、4 B、3 C、2 D、113. 阅读理解:设 ,若 ,则 ,即 ,已知 =(-2,x+1), =(3,x+2),且 ,则x的值为( )A、2或-2 B、1或-4 C、-1或4 D、114. 如图,在Rt 中,OA=OB=4 ,⊙O的半径为2, 点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长的最小值为( )
A、4 B、3 C、2 D、113. 阅读理解:设 ,若 ,则 ,即 ,已知 =(-2,x+1), =(3,x+2),且 ,则x的值为( )A、2或-2 B、1或-4 C、-1或4 D、114. 如图,在Rt 中,OA=OB=4 ,⊙O的半径为2, 点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长的最小值为( )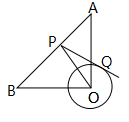 A、2 B、 C、1 D、2
A、2 B、 C、1 D、2二、填空题
-
15. 关于x的方程kx2+3x-1=0有实数根,则k的取值范围是.16. 函数y=2x2-8x+1的最小值是.17. 在⊙O中,若弦 垂直平分半径 ,则弦 所对的圆周角等于°.18. 如图, 中, ,点D是斜边上任意一点,将点D绕点C逆时针旋转 得到点E , 则线段DE长度的最小值是 .
 19. 如图是足球守门员在O处开出一记手抛高球后足球在空中运动到落地的过程,它是一条经过A、M、C三点的抛物线.其中A点离地面1.4米,M点是足球运动过程中的最高点,离地面3.2米,离守门员的水平距离为6米,点C是球落地时的第一点.那么足球第一次落地点C距守门员的水平距离为米.
19. 如图是足球守门员在O处开出一记手抛高球后足球在空中运动到落地的过程,它是一条经过A、M、C三点的抛物线.其中A点离地面1.4米,M点是足球运动过程中的最高点,离地面3.2米,离守门员的水平距离为6米,点C是球落地时的第一点.那么足球第一次落地点C距守门员的水平距离为米.
三、解答题
-
20. 已知关于x的方程x2+ax+a﹣3=0.(1)、若该方程的一个根为2,求a的值及方程的另一个根;(2)、求证:不论a取何实数,该方程都有两个不相等的实数根.21. 如图,在△ 中,三个顶点的坐标分别为A(2,3),B(5, ),C(1,1),将△ 向左平移4个单位长度,再向下平移2个单位长度,得到△ ,其中点A的对应点为点D,点B的对应点为点E,点C的对应点为点F.
 (1)、直接写出平移后的△ 的顶点坐标:D、E、F;(2)、在网格中画出△ABC绕原点顺时针旋转90°后的图形△A1B1C1;(3)、求出△A1B1C1的面积.22. 某地区在2020年开展脱贫攻坚的工作中大力种植有机蔬菜.某种蔬菜的销售单价与销售月份之间的关系如图(1)所示,每千克成本与销售月份之间的关系如图(2)所示.(其中图(1)的图象是直线,图(2)的图象是抛物线,其最低点坐标是(6,1)).
(1)、直接写出平移后的△ 的顶点坐标:D、E、F;(2)、在网格中画出△ABC绕原点顺时针旋转90°后的图形△A1B1C1;(3)、求出△A1B1C1的面积.22. 某地区在2020年开展脱贫攻坚的工作中大力种植有机蔬菜.某种蔬菜的销售单价与销售月份之间的关系如图(1)所示,每千克成本与销售月份之间的关系如图(2)所示.(其中图(1)的图象是直线,图(2)的图象是抛物线,其最低点坐标是(6,1)). (1)、求每千克蔬菜销售单价y与销售月份x之间的关系式;(2)、判断哪个月份销售每千克蔬菜的收益最大?并求最大收益;(3)、求出一年中销售每千克蔬菜的收益大于1元的月份有哪些?23. 如图,O为菱形 ABCD对角线上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点M .
(1)、求每千克蔬菜销售单价y与销售月份x之间的关系式;(2)、判断哪个月份销售每千克蔬菜的收益最大?并求最大收益;(3)、求出一年中销售每千克蔬菜的收益大于1元的月份有哪些?23. 如图,O为菱形 ABCD对角线上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点M . (1)、求证:CD与⊙O相切;(2)、若菱形ABCD的边长为1,∠ABC=60°,求⊙O的半径.
(1)、求证:CD与⊙O相切;(2)、若菱形ABCD的边长为1,∠ABC=60°,求⊙O的半径.