山东省滨州市滨城区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-12-01 类型:期中考试
一、单选题
-
1. 下列方程一定是一元二次方程的是( )A、x2+ ﹣1=0 B、2x2﹣y﹣3=0 C、ax2﹣x+2=0 D、3x2﹣2x﹣1=02. 我国民间,流传着许多含有吉祥意义的文字图案,表示对幸福生活的向往,良辰佳节的祝贺.比如下列图案分别表示“福”、“禄”、“寿”、“喜”,其中是轴对称图形,但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 将抛物线 平移,得到抛物线 ,下列平移方式中,正确的是( )A、先向左平移1个单位,再向上平移2个单位 B、先向左平移1个单位,再向下平移2个单位 C、先向右平移1个单位,再向上平移2个单位 D、先向右平移1个单位,再向下平移2个单位4. 一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是( )A、 B、 C、 D、5. 如图,AB是⊙O的直径,C,D是圆上两点,连接AC,BC,AD,CD.若∠CAB=55°,则∠ADC的度数为( )
3. 将抛物线 平移,得到抛物线 ,下列平移方式中,正确的是( )A、先向左平移1个单位,再向上平移2个单位 B、先向左平移1个单位,再向下平移2个单位 C、先向右平移1个单位,再向上平移2个单位 D、先向右平移1个单位,再向下平移2个单位4. 一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是( )A、 B、 C、 D、5. 如图,AB是⊙O的直径,C,D是圆上两点,连接AC,BC,AD,CD.若∠CAB=55°,则∠ADC的度数为( ) A、55° B、45° C、35° D、25°6. 用等腰直角三角板画∠AOB=45°,将三角板沿OB方向平移到如图所示的虚线M处后绕点M逆时针旋转22°,则三角板的斜边与射线OA的夹角α为( )度.
A、55° B、45° C、35° D、25°6. 用等腰直角三角板画∠AOB=45°,将三角板沿OB方向平移到如图所示的虚线M处后绕点M逆时针旋转22°,则三角板的斜边与射线OA的夹角α为( )度.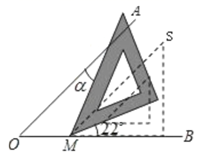 A、25° B、45° C、30° D、22°7. 一枚炮弹射出x秒后的高度为y米,且y与x之间的关系为y=ax2+bx+c(a≠0),若此炮弹在第3.2秒与第5.8秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )A、第3.3s B、第4.3s C、第5.2s D、第4.6s8. 对于二次函数y=﹣3(x+2k)2+k(a≠0)而言,无论k取何实数,其图象的顶点都在( )A、x轴上 B、直线y=﹣x上 C、直线y= x D、直线y= x上9. 已知关于x的一元二次方程x2+ax+b=0有一个非零根﹣b , 则a﹣b的值为( )A、1 B、﹣1 C、2 D、﹣210. 设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1 , y2 , y3的大小关系为( )A、y1>y2>y3 B、y1>y3>y2 C、y3>y2>y1 D、y3>y1>y211. 已知PA , PB是⊙O的切线,A , B是切点,点C是⊙O上不同于点A、点B的一个动点,若∠P=54°,则∠ACB的度数是( )A、63° B、117° C、53°或127° D、117°或63°12. 如图,弧长为半圆的弓形在坐标系中,圆心在 .将弓形沿x轴正方向无滑动滚动,当圆心经过的路径长为 时,圆心的横坐标是( )
A、25° B、45° C、30° D、22°7. 一枚炮弹射出x秒后的高度为y米,且y与x之间的关系为y=ax2+bx+c(a≠0),若此炮弹在第3.2秒与第5.8秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )A、第3.3s B、第4.3s C、第5.2s D、第4.6s8. 对于二次函数y=﹣3(x+2k)2+k(a≠0)而言,无论k取何实数,其图象的顶点都在( )A、x轴上 B、直线y=﹣x上 C、直线y= x D、直线y= x上9. 已知关于x的一元二次方程x2+ax+b=0有一个非零根﹣b , 则a﹣b的值为( )A、1 B、﹣1 C、2 D、﹣210. 设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1 , y2 , y3的大小关系为( )A、y1>y2>y3 B、y1>y3>y2 C、y3>y2>y1 D、y3>y1>y211. 已知PA , PB是⊙O的切线,A , B是切点,点C是⊙O上不同于点A、点B的一个动点,若∠P=54°,则∠ACB的度数是( )A、63° B、117° C、53°或127° D、117°或63°12. 如图,弧长为半圆的弓形在坐标系中,圆心在 .将弓形沿x轴正方向无滑动滚动,当圆心经过的路径长为 时,圆心的横坐标是( )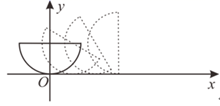 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 一个底面直径是80cm,母线长为90cm的圆锥的侧面展开图的圆心角的度数为 .
14. 已知一元二次方程(a﹣1)x2+a2+3a﹣4=0有一个根为零,则a的值为 .15. 在半径为2的⊙O中,弦AB为2,则弦AB所对的圆周角的度数为 .16. 如图,在平面直角坐标系xOy中,直线y1=kx+m(k≠0)的抛物线y2=ax2+bx+c(a≠0)交于点A(0,4),B(3,1),当y1≤y2时,x的取值范围是 . 17. 如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A , B两点,点P在 上.请写出经过A、B且以点P为顶点的抛物线解析式 .
17. 如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A , B两点,点P在 上.请写出经过A、B且以点P为顶点的抛物线解析式 .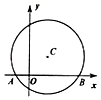 18. 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),该抛物线的部分图象如图所示,下列结论:①4ac<b2; ②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3; ③3a+c>0; ④当x<0时,y随x增大而减小;⑤点P(m , n)是抛物线上任意一点,则m(am+b)≤a+b , 其中正确的结论是 .(填写序号)
18. 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),该抛物线的部分图象如图所示,下列结论:①4ac<b2; ②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3; ③3a+c>0; ④当x<0时,y随x增大而减小;⑤点P(m , n)是抛物线上任意一点,则m(am+b)≤a+b , 其中正确的结论是 .(填写序号)
三、解答题
-
19. 用适当的方法解下列方程.(1)、x2﹣4x+2=0.(2)、x2﹣6x+9=(5﹣2x)2 .20. 不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中红球有2个,蓝球有1个,现从中任意摸出一个是红球的概率为 .(1)、求袋中黄球的个数;(2)、第一次摸出一个球(不放回),第二次再摸一个小球,请用画树状图或列表法求两次摸到都是红球的概率;(3)、若规定摸到红球得5分,摸到黄球得3分,摸到蓝球得1分,小明共摸6次小球(每次摸1个球,摸后放回)得20分,问小明有哪几种摸法?21. 如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
 (1)、请画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标;(2)、请画出△ABC绕点B逆时针旋转90∘后的△A2BC2;(3)、求出 (2)中C点旋转到C2点所经过的路径长(结果保留根号和π).(4)、在x轴上有一点P,PA+PB的值最小,请直接写出点P的坐标22. 已知:如图,点A , B , C三点在⊙O上,AE平分∠BAC , 交⊙O于点E , 交BC于点D , 过点E作直线l∥BC , 连结BE .
(1)、请画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标;(2)、请画出△ABC绕点B逆时针旋转90∘后的△A2BC2;(3)、求出 (2)中C点旋转到C2点所经过的路径长(结果保留根号和π).(4)、在x轴上有一点P,PA+PB的值最小,请直接写出点P的坐标22. 已知:如图,点A , B , C三点在⊙O上,AE平分∠BAC , 交⊙O于点E , 交BC于点D , 过点E作直线l∥BC , 连结BE . (1)、求证:直线l是⊙O的切线;.(2)、如果∠BAC=60°,AB=6,AC=8,求AE的长.23. 为做好新冠疫情的防控工作,某单位需购买甲、乙两种消毒液经了解每桶甲种消毒液的零售价比乙种消毒液的零售价多6元,该单位以零售价分别用900元和720元采购了相同桶数的甲、乙两种消毒液.(1)、求甲、乙两种消毒液的零售价分别是每桶多少元?(2)、由于疫情防控进入常态化,该单位需再次购买两种消毒液共300桶,且甲种消毒液的桶数不少于乙种消毒液桶数的 ,由于购买量大,甲、乙两种消毒液分别获得了20元/桶,15元/桶的批发价.求甲种消毒液购买多少桶时,所需资金总额最少?最少总金额是多少元?24. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B .
(1)、求证:直线l是⊙O的切线;.(2)、如果∠BAC=60°,AB=6,AC=8,求AE的长.23. 为做好新冠疫情的防控工作,某单位需购买甲、乙两种消毒液经了解每桶甲种消毒液的零售价比乙种消毒液的零售价多6元,该单位以零售价分别用900元和720元采购了相同桶数的甲、乙两种消毒液.(1)、求甲、乙两种消毒液的零售价分别是每桶多少元?(2)、由于疫情防控进入常态化,该单位需再次购买两种消毒液共300桶,且甲种消毒液的桶数不少于乙种消毒液桶数的 ,由于购买量大,甲、乙两种消毒液分别获得了20元/桶,15元/桶的批发价.求甲种消毒液购买多少桶时,所需资金总额最少?最少总金额是多少元?24. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B . (1)、求二次函数y=ax2+bx+c的表达式;(2)、过点A作AC平行于x轴,交抛物线于点C , 点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D , 问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(1)、求二次函数y=ax2+bx+c的表达式;(2)、过点A作AC平行于x轴,交抛物线于点C , 点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D , 问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;