黑龙江省齐齐哈尔市建华区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-12-01 类型：期中考试

进入出卷网下载

一、单选题

1. 下列汽车标志图片中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 一元二次方程（x-3)(x-5)=0的两根分别为( )

A、3 , －5 B、－3，－5 C、－3 , 5 D、3 ，5

查看试题解析
3. 如图， $⊙ O$ 的弦AB垂直平分半径OC ，若 $A B = 6 \sqrt{3}$ ，则 $⊙ O$ 的半径为（　　）

A、3 B、 $3 \sqrt{3}$ C、 $\frac{3}{2} \sqrt{3}$ D、6

查看试题解析
4. 关于x的方程x²+2kx+k﹣1=0的根的情况描述正确的是（　　）

A、k为任何实数，方程都没有实数根 B、k为任何实数，方程都有两个不相等的实数拫 C、k为任何实数，方程都有两个相等的实数根 D、根据k的取值不同，方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种

查看试题解析
5. 如图所示，图中的每个阴影旋转一个角度后都能互相重合，这个角度可能是（　　）

A、30° B、45° C、120° D、90°

查看试题解析
6. 已知一元二次方程x²+bx﹣3＝0的一个根是﹣3，若二次函数y＝x²+bx﹣3的图象上有三个点 $(- \frac{5}{6} ， y_{1})$ 、 $(- \frac{6}{5} ， y_{2})$ 、 $(- \frac{1}{3} ， y_{3})$ ，则y₁ ， y₂ ， y₃的大小关系为（　　）

A、y₁＜y₂＜y₃ B、y₂＜y₁＜y₃ C、y₃＜y₁＜y₂ D、y₁＜y₃＜y₂

查看试题解析
7. 下列命题中，正确的是（）
①顶点在圆周上的角是圆周角；②圆周角的度数等于圆心角度数的一半；③ $90^{\circ}$ 的圆周角所对的弦是直径；④不在同一条直线上的三个点确定一个圆；⑤同弧所对的圆周角相等

A、①②③ B、③④⑤ C、①②⑤ D、②④⑤

查看试题解析
8. 关于 $x$ 的一元二次方程 $x^{2} - 3 x + m = 0$ 有两个不相等的实数根，则实数 $m$ 的取值范围是 $($ $)$

A、 $m < \frac{9}{4}$ B、 $m ⩽ \frac{9}{4}$ C、 $m > \frac{9}{4}$ D、 $m ⩾ \frac{9}{4}$

查看试题解析
9. 如图，在平面直角坐标系中，过边长为1的正方形格点A、B、C作一圆弧，点B与下列格点的连线中，能够与该圆弧相切的是（　　）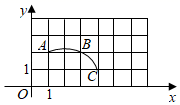

A、点（5，0） B、点（2，3） C、点（6，1） D、点（1，3）

查看试题解析
10. 如图所示，二次函数y＝ax²+bx+c（a≠0）的图象经过点A（﹣1，2），且与x轴交点的横坐标分别为x₁ ， x₂ ，其中﹣2＜x₁＜﹣1，0＜x₂＜1，下列四个结论①2a﹣b＜0；②4a﹣2b+c＜0；③c﹣a＞2；④3a+c＞0中，错误的有（　　）个．

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

11. 同圆中，已知弧AB所对的圆心角是100°，则弧AB所对的圆周角是．

查看试题解析
12. 已知点（1，0）是y＝x²+bx﹣2的图象上一点，则方程x²+bx﹣2＝0的根是．

查看试题解析
13. 一个扇形的圆心角为135°，弧长为3πcm，则此扇形的面积是cm².

查看试题解析
14. 如图，在矩形ABCD中，AD=3，将矩形ABCD绕点A逆时针旋转，得到矩形AEFG，点B的对应点E落在CD上，且DE=EF，则AB的长为．

查看试题解析
15. 四位同学在研究函数y＝x²+bx+c（b、c是常数）时，小红发现当x＝1时，函数有最小值；小明发现﹣1是方程x²+bx+c＝0的一个根；小聪发现函数的最小值为3；小睿发现当x＝2时，y＝4．若这四位同学中有且只有一位同学发现的结论是错误的，则该同学是．

查看试题解析
16. 如图，点A在x轴的正半轴上运动，点B在y轴的正半轴上，OB＝2，连接AB ， △ABP与△ABO关于直线AB对称．点C、点D分别是BO、BA的中点，连接CD并延长交PA于点E ，连接PD ，当点P的坐标为时，△PDE为直角三角形．

查看试题解析
17. 在如图所示的平面直角坐标系内，已知△OA₁B₁中，点A₁、点B₁的坐标分别为A₁（1，1）、B₁（1，0），将线段OA₁绕点O逆时针旋转，使OA₁落在y轴的正半轴上得到线段OB₂ ，以OB₂为直角边作等腰直角三角形△OB₂A₂ ，且斜边OA₂在第二象限；再将线段OA₂绕点O逆时针旋转，使OA₂落在x轴的负半轴上得到线段OB₃ ，以OB₃为直角边作等腰直角三角形△OB₃A₃ ，且斜边OA₃在第三象限：……，如此作下去，则点A₂₀₂₁的坐标为．

查看试题解析

三、解答题

18. 解方程

(1)、 $\frac{1}{2}$ x（x﹣1）＝55

(2)、（3x﹣2）（x+1）＝x（2x﹣1）

查看试题解析
19. 如图，方格纸中的每个小方格都是边长为1单位的正方形，在建立如图所示的平面直角坐标系后，△ABC的顶点均在格点上，且坐标分别为：A（2，2）、B（﹣1，﹣1）、C（3，﹣1）．依据所给信息，解决下列问题：

(1)、请你画出将△ABC向右平移6个单位后得到对应的△A₁B₁C₁；

(2)、再请你画出将△A₁B₁C₁绕点B₁顺时针旋转90°后得到的△A₂B₂C₂；

(3)、求四边形A₂B₁CC₂的面积．

查看试题解析
20. 如图，四边形ABCD中，∠B＝∠D ， AB＝CD ， AB与DC不平行，过点A作 $A E ∥ D C$ ，交△ABC的外接圆⊙O于点E ，连接CE、OA ．

(1)、求证：四边形ADCE为平行四边形；

(2)、求证：AO平分∠BAE ．

查看试题解析
21. 如图，以60米/秒的速度将小球沿与地面成30°角的方向击出时，小球的飞行路线将是一条抛物线．若不考虑空气阻力，小球的飞行高度h（单位：米）与飞行时间t（单位：秒）之间有下列函数关系：h＝30t﹣5t².依据所给信息，解决下列问题：

(1)、小球的飞行高度是否能达到25米？如果能，需要飞行的时间是多少？

(2)、小球的飞行高度是否能达到45米？如果能，需要飞行的时间是多少？请直接写出答案：．

(3)、小球从飞出到落地要用多少时间（设地面是水平的）？

查看试题解析
22. 如图，在△ABC中，O为AC上的一点，以点O为圆心OC为半径的⊙O ，与BC相切于点C ，过点A作AD⊥BO交BO的延长线于点D ，且∠AOD＝∠BAD ．

(1)、求证：AB为⊙O的切线；

(2)、若∠BAD＝60°，⊙O的半径为3，则AD＝.点D与⊙O的位置关系为．

查看试题解析
23. 抛物线y＝﹣x²+bx+c经过A（0，1）、B（4，3）两点，顶点为点P ，连接PA ， PB ．

(1)、求抛物线及直线AB的解析式；

(2)、请你直接写出△PAB的面积；

(3)、过点B作BC⊥x轴，垂足为C ，平行于y轴的直线交直线AB于点N ，交抛物线于点M ，否存在点M ，使以点B、点C、点M、点N为顶点的四边形为平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．

查看试题解析