广东省揭阳市普宁市2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-12-01 类型:期中考试
一、单选题
-
1. 已知 ,那么下列比例式中成立的是( )A、 B、 C、 D、2. 已知2是关于x的方程3x2﹣2a=0的一个解,则a的值是( )A、3 B、4 C、5 D、63. 已知菱形的边长和一条对角线的长均为2cm,则菱形的面积为( )A、3cm2 B、4cm2 C、 cm2 D、2 cm24. 如图,直线 ,直线AC和DF被 , , 所截, , , ,则 的长为( ).
 A、2 B、3 C、4 D、5. 为了庆祝中国共产党成立100周年,某校举办了党史知识竞赛活动,在获得一等奖的学生中,有3名女学生,1名男学生,则从这4名学生中随机抽取2名学生,恰好抽到2名女学生的概率为( )A、 B、 C、 D、6. 如图,点 是线段 的黄金分割点( ),下列结论错误的是( )
A、2 B、3 C、4 D、5. 为了庆祝中国共产党成立100周年,某校举办了党史知识竞赛活动,在获得一等奖的学生中,有3名女学生,1名男学生,则从这4名学生中随机抽取2名学生,恰好抽到2名女学生的概率为( )A、 B、 C、 D、6. 如图,点 是线段 的黄金分割点( ),下列结论错误的是( )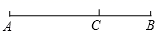 A、 B、 C、 D、7. 用配方法解方程时,下列配方错误的是( ).A、 化为 B、 化为 C、 化为 D、 化为8. 如图, ,其中 , , ,M为BC中点,EF过点M交AC、BD于点E、F , 连接BE、CF , 则下列结论错误的是( ).
A、 B、 C、 D、7. 用配方法解方程时,下列配方错误的是( ).A、 化为 B、 化为 C、 化为 D、 化为8. 如图, ,其中 , , ,M为BC中点,EF过点M交AC、BD于点E、F , 连接BE、CF , 则下列结论错误的是( ). A、四边形BECF为平行四边形 B、当 时,四边形BECF为矩形 C、当 时,四边形BECF为菱形 D、四边形BECF不可能为正方形9. 如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为600平方米,则小道的宽为多少米?若设小道的宽为 米,则根据题意,列方程为( )
A、四边形BECF为平行四边形 B、当 时,四边形BECF为矩形 C、当 时,四边形BECF为菱形 D、四边形BECF不可能为正方形9. 如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为600平方米,则小道的宽为多少米?若设小道的宽为 米,则根据题意,列方程为( ) A、 B、 C、 D、10. 如图,在边长为 的等边 中,分别取 三边的中点 , , ,得△ ;再分别取△ 三边的中点 , , ,得△ ;这样依次下去 ,经过第2021次操作后得△ ,则△ 的面积为( )
A、 B、 C、 D、10. 如图,在边长为 的等边 中,分别取 三边的中点 , , ,得△ ;再分别取△ 三边的中点 , , ,得△ ;这样依次下去 ,经过第2021次操作后得△ ,则△ 的面积为( )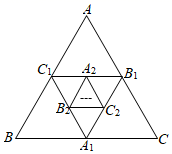 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 一元二次方程 的两根是 .12. 如图,∠DAB=∠CAE,请补充一个条件: , 使△ABC∽△ADE.
 13. 如图,在正方形 ,E是对角线 上一点, 的延长线交 于点F,连接 .若 ,则 .
13. 如图,在正方形 ,E是对角线 上一点, 的延长线交 于点F,连接 .若 ,则 . 14. 如图,小华同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,使斜边DF与地面保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边 , ,测得边DF离地面的高度 , ,则树AB的高度为cm.
14. 如图,小华同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,使斜边DF与地面保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边 , ,测得边DF离地面的高度 , ,则树AB的高度为cm. 15. 已知a、b是一元二次方程 的两个根,则 的值为 .16. 如图,在 中, ,点D , E分别在边AB , AC上, , 且 ,则 .
15. 已知a、b是一元二次方程 的两个根,则 的值为 .16. 如图,在 中, ,点D , E分别在边AB , AC上, , 且 ,则 . 17. 如图,在矩形ABCD中, ,点E , F分别在BC , CD上,将 沿AE折叠,使点B落在AC上的点 处,又将 沿EF折叠,使点C落在直线 与AD的交点 处, .
17. 如图,在矩形ABCD中, ,点E , F分别在BC , CD上,将 沿AE折叠,使点B落在AC上的点 处,又将 沿EF折叠,使点C落在直线 与AD的交点 处, .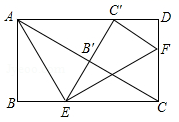
三、解答题
-
18. 解方程: .19. 已知:如图,在菱形ABCD中,E , F分别是边AD和CD上的点,且 .求证:
 20. 如图,已知∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.
20. 如图,已知∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.求证:△ABC∽△AED.
 21. 小明和小刚一起做游戏,游戏规则如下:将分别标有数字 1, 2, 3, 4 的 4 个小球放入一个不透明的袋子中,这些球除数字外都相同.从中随机摸出一个球记下数字后放回,再从中随机摸出一个球记下数字.若两次数字差的绝对值小于 2,则小明获胜,否则小刚获胜.这个游戏对两人公平吗?请说明理由.22. 关于 的一元二次方程 有实数根.(1)、求 的取值范围;(2)、如果 是符合条件的最大整数,且一元二次方程 与方程 有一个相同的根,求此时 的值.23. 2020年年初以来,全国多地猪肉价格连续上涨,引起了民众与政府的高度关注,政府向市场投入储备猪肉进行了价格平抑.据统计:某超市2020年1月10日猪肉价格比去年同一天上涨了40%,这天该超市每千克猪肉价格为56元.
21. 小明和小刚一起做游戏,游戏规则如下:将分别标有数字 1, 2, 3, 4 的 4 个小球放入一个不透明的袋子中,这些球除数字外都相同.从中随机摸出一个球记下数字后放回,再从中随机摸出一个球记下数字.若两次数字差的绝对值小于 2,则小明获胜,否则小刚获胜.这个游戏对两人公平吗?请说明理由.22. 关于 的一元二次方程 有实数根.(1)、求 的取值范围;(2)、如果 是符合条件的最大整数,且一元二次方程 与方程 有一个相同的根,求此时 的值.23. 2020年年初以来,全国多地猪肉价格连续上涨,引起了民众与政府的高度关注,政府向市场投入储备猪肉进行了价格平抑.据统计:某超市2020年1月10日猪肉价格比去年同一天上涨了40%,这天该超市每千克猪肉价格为56元. (1)、求2019年1月10日,该超市猪肉的价格为每千克多少元?(2)、现在某超市以每千克46元的价格购进猪肉,按2020年1月10日价格出售,平均一天能销售100千克.经调查表明:猪肉的售价每千克下降1元,平均每日销售量就增加20千克,超市为了实现销售猪肉平均每天有1120元的销售利润,在尽可能让利于顾客的前提下,每千克猪肉应该定价为多少元?24. 如图,已知矩形ABCD的边长AB=3cm,BC=6cm,某一时刻,动点M从点A出发沿AB方向以1cm/s的速度向点B匀速运动;同时,动点N从点D沿DA方向以2cm/s的速度向点A匀速运动.
(1)、求2019年1月10日,该超市猪肉的价格为每千克多少元?(2)、现在某超市以每千克46元的价格购进猪肉,按2020年1月10日价格出售,平均一天能销售100千克.经调查表明:猪肉的售价每千克下降1元,平均每日销售量就增加20千克,超市为了实现销售猪肉平均每天有1120元的销售利润,在尽可能让利于顾客的前提下,每千克猪肉应该定价为多少元?24. 如图,已知矩形ABCD的边长AB=3cm,BC=6cm,某一时刻,动点M从点A出发沿AB方向以1cm/s的速度向点B匀速运动;同时,动点N从点D沿DA方向以2cm/s的速度向点A匀速运动. (1)、经过多少时间,△AMN的面积等于矩形ABCD面积的 ?(2)、是否存在时刻t,使A、M、N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.25. 如图①,在正方形 中, , 为对角线 上任意一点(不与 重合),连接 ,过点 作 ,交线段 于点 .
(1)、经过多少时间,△AMN的面积等于矩形ABCD面积的 ?(2)、是否存在时刻t,使A、M、N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.25. 如图①,在正方形 中, , 为对角线 上任意一点(不与 重合),连接 ,过点 作 ,交线段 于点 . (1)、求证: ;(2)、若 ,求证: ;(3)、如图②,连接 交 于点 .若 ,求 的值.
(1)、求证: ;(2)、若 ,求证: ;(3)、如图②,连接 交 于点 .若 ,求 的值.