北京市大兴区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-12-01 类型:期中考试
一、单选题
-
1. 北京时间2021年10月16日0时23分,长征二号 运载火箭托举神舟十三号载人飞船升空,中国空间站关键技术验证阶段收官之战正式打响.长征二号 运载火箭是长征家族的明星火箭,绰号“神箭”.它的身高58米,体重497吨,运载能力超过 吨,起飞推力 牛,它是中国航天员的专属交通工具.将 用科学记数法表示应为( )A、 B、 C、 D、2. 抛物线 的顶点坐标是( )A、 B、 C、 D、3. 方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定是否有实数根4. 如图,把菱形ABOC绕点O顺时针旋转得到菱形DFOE,则下列角中不是旋转角的为( )
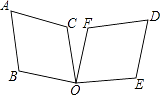 A、∠BOF B、∠AOD C、∠COE D、∠COF5. 已知抛物线 经过点 , ,则 与 的大小关系是( )A、 B、 C、 D、6. 用配方法解方程 ,变形后的结果正确的是( )A、 B、 C、 D、7. 将抛物线 向左平移 个单位长度,再向下平移 个单位长度后,就得到抛物线( )A、 B、 C、 D、8. 某种商品的价格是 元,准备进行两次降价.如果每次降价的百分率都是 ,经过两次降价后的价格 (单位:元)随每次降价的百分率 的变化而变化,则 关于 的函数解析式是( )A、 B、 C、 D、
A、∠BOF B、∠AOD C、∠COE D、∠COF5. 已知抛物线 经过点 , ,则 与 的大小关系是( )A、 B、 C、 D、6. 用配方法解方程 ,变形后的结果正确的是( )A、 B、 C、 D、7. 将抛物线 向左平移 个单位长度,再向下平移 个单位长度后,就得到抛物线( )A、 B、 C、 D、8. 某种商品的价格是 元,准备进行两次降价.如果每次降价的百分率都是 ,经过两次降价后的价格 (单位:元)随每次降价的百分率 的变化而变化,则 关于 的函数解析式是( )A、 B、 C、 D、二、填空题
-
9. 分解因式:ab2﹣4ab+4a= .10. 若关于 的一元二次方程 有一根为 ,则 .11. 已知点 与点 关于原点对称,则a= .12. 一元二次方程 的根是 .13. 请写出一个开口向下,并且与 轴交于点 的抛物线的解析式 .14. 如图,△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得C′C∥AB , 则∠BAB′等于 .
 15. 抛物线 与 的一个交点坐标是 ,则另一个交点坐标是 .16. 如图,直线 与 轴、 轴分别交于 、 两点,把 绕点 旋转 后得到 ,则点 的坐标是 .
15. 抛物线 与 的一个交点坐标是 ,则另一个交点坐标是 .16. 如图,直线 与 轴、 轴分别交于 、 两点,把 绕点 旋转 后得到 ,则点 的坐标是 .
三、解答题
-
17. 解方程:18. 已知点 是二次函数 图象上一点,求代数式 的值.19. 已知二次函数 .
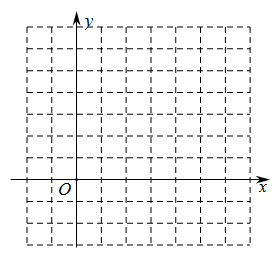 (1)、二次函数 的图象与 轴交于 、 两点( 点在 点左侧),求 、 两点的坐标;(2)、在网格中,画出该函数的图象.20. 已知二次函数 ,函数 与自变量 的部分对应值如下表:
(1)、二次函数 的图象与 轴交于 、 两点( 点在 点左侧),求 、 两点的坐标;(2)、在网格中,画出该函数的图象.20. 已知二次函数 ,函数 与自变量 的部分对应值如下表:…
-1
0
1
2
3
4
…
…
0
-3
-4
-3
0
5
…
(1)、求该二次函数的解析式;(2)、当 为何值时 有最小值,最小值是多少?21. 已知关于 的一元二次方程 有两个不相等的实数根.(1)、求 的取值范围;(2)、当 取满足条件的最大整数时,求方程的根.22. 在体育课掷实心球活动中,小华通过研究发现:实心球所经过的路线是一条抛物线的一部分,如果球出手处点 距离地面的高度为 ,当球运行的水平距离为 时,达到最大高度 的 处(如图),问实心球的落地点 与出手处点 的水平距离是多少?(结果保留根号) 23. 在平面直角坐标系 中,抛物线 与 轴交于点 .
23. 在平面直角坐标系 中,抛物线 与 轴交于点 . (1)、点 的坐标是;(2)、横、纵坐标都是整数的点叫做整点.直接写出抛物线 与直线 围成的阴影图形中(不包括边界)所含的所有整点的坐标.24. 中, ,以点A为中心,分别将线段 , 逆时针旋转 得到线段 , ,连接 ,延长 交 于点 .用等式表示线段 与 的数量关系,并加以证明.
(1)、点 的坐标是;(2)、横、纵坐标都是整数的点叫做整点.直接写出抛物线 与直线 围成的阴影图形中(不包括边界)所含的所有整点的坐标.24. 中, ,以点A为中心,分别将线段 , 逆时针旋转 得到线段 , ,连接 ,延长 交 于点 .用等式表示线段 与 的数量关系,并加以证明. 25. 大兴某小区为响应创建文明城市号召,引导小区居民节约用水,居委会工作人员小赵在该小区的1000个家庭中,随机统计了 个家庭的月用水情况,并绘制了如下的频数分布表(其中 为每个家庭的月用水量,单位:吨).
25. 大兴某小区为响应创建文明城市号召,引导小区居民节约用水,居委会工作人员小赵在该小区的1000个家庭中,随机统计了 个家庭的月用水情况,并绘制了如下的频数分布表(其中 为每个家庭的月用水量,单位:吨).月用水量 /吨
频数
8
20
14
6
2
合计
请你根据以上提供的信息,解答下列问题:
(1)、 的值为;(2)、计算该小区1000个家庭中月用水量 的家庭大约有多少个.26. 在平面直角坐标系 中,已知抛物线 ( ).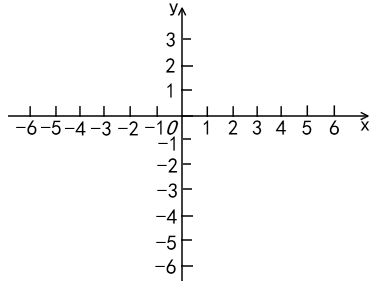 (1)、求抛物线的对称轴;(2)、若方程 ( )有两个不相等的实数根 , ,且 ,结合函数的图象,求 的取值范围.27. 已知在 中, , ,在平面内有一个点 (点 与点 , 不重合),以点 为中心,把线段 顺时针旋转 ,得到线段 ,连接 , .(1)、如图,若点 在边 上;
(1)、求抛物线的对称轴;(2)、若方程 ( )有两个不相等的实数根 , ,且 ,结合函数的图象,求 的取值范围.27. 已知在 中, , ,在平面内有一个点 (点 与点 , 不重合),以点 为中心,把线段 顺时针旋转 ,得到线段 ,连接 , .(1)、如图,若点 在边 上;①依题意补全图形;

②设 ,则 .
(2)、如图,若点 不在边 上,猜想线段 , 之间的数量关系及位置关系,并证明. 28. 定义:在平面直角坐标系 中,抛物线 ( )与 轴交于点 , .点 为平面内任意一点,若 ,且 时,称点 为线段 的“居中点”.特别地,当 ,且 时,又称点 为线段 的“正居中点”.抛物线 与 轴的正半轴交于点 .
28. 定义:在平面直角坐标系 中,抛物线 ( )与 轴交于点 , .点 为平面内任意一点,若 ,且 时,称点 为线段 的“居中点”.特别地,当 ,且 时,又称点 为线段 的“正居中点”.抛物线 与 轴的正半轴交于点 . (1)、若点 是线段 的“正居中点”,且在第一象限,则点 的坐标为;(2)、若点 是线段 的“居中点”,则点 的纵坐标 的取值范围是;(3)、将射线 绕点 顺时针旋转 得到射线 ,已知点 在射线 上,若在第四象限内存在点 ,点 既是线段 的“居中点”,又是线段 的“正居中点”,求此时点 的坐标.
(1)、若点 是线段 的“正居中点”,且在第一象限,则点 的坐标为;(2)、若点 是线段 的“居中点”,则点 的纵坐标 的取值范围是;(3)、将射线 绕点 顺时针旋转 得到射线 ,已知点 在射线 上,若在第四象限内存在点 ,点 既是线段 的“居中点”,又是线段 的“正居中点”,求此时点 的坐标.