安徽省合肥市包河区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-12-01 类型:期中考试
一、单选题
-
1. 函数 图象的顶点坐标是( )A、 B、 C、 D、2. 如果 ,则下列结论错误的是( )A、 B、 C、 D、3. 将抛物线 沿y轴向下平移2个单位,得到的抛物线的解析式为 ( )A、 B、 C、 D、4. 比值为 (约0.618)的比例被公认为是最能引起美感的比例,因此被称为黄金分割比,我们中国的国旗宽与长之比就非常接近这个比例,如果某面国旗长为2米,则其宽约为( )A、1.4米 B、1.2米 C、1.0米 D、0.8米5. 如图,线段 两个端点的坐标分别为 ,以原点O为位似中心,在第一象限内将线段 扩大为原来的2倍后得到线段 ,则端点C的坐标为( )
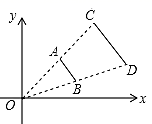 A、 B、 C、 D、6. 已知二次函数 图象上的三点 ,则 的大小关系为( )A、 B、 C、 D、7. 在 中,D为 边上一点,则下列条件一定能得到一对相似三角形的是( )A、 B、 C、 D、8. 如图,在 中,D、E分别是边 、 上的点, 与 相交于点F , 若E为 的中点, ,则 的值是( )
A、 B、 C、 D、6. 已知二次函数 图象上的三点 ,则 的大小关系为( )A、 B、 C、 D、7. 在 中,D为 边上一点,则下列条件一定能得到一对相似三角形的是( )A、 B、 C、 D、8. 如图,在 中,D、E分别是边 、 上的点, 与 相交于点F , 若E为 的中点, ,则 的值是( ) A、2.5 B、3 C、4 D、29. 如图, 中, , , 为 边上的中线,E , F分别为 边上的点,且 ,过F点作 于点G . 以下结论:① ② ③ ④ 其中正确结论的个数是( )
A、2.5 B、3 C、4 D、29. 如图, 中, , , 为 边上的中线,E , F分别为 边上的点,且 ,过F点作 于点G . 以下结论:① ② ③ ④ 其中正确结论的个数是( ) A、1 B、2 C、3 D、410. 如图,直线l为抛物线 的对称轴,点P为抛物线上一动点(在顶点或顶点的右侧),过点P作 轴于点A , 作PB∥x轴交抛物线于点B , 设 , ,则h与m的函数图象大致为( )
A、1 B、2 C、3 D、410. 如图,直线l为抛物线 的对称轴,点P为抛物线上一动点(在顶点或顶点的右侧),过点P作 轴于点A , 作PB∥x轴交抛物线于点B , 设 , ,则h与m的函数图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 二次函数 的最小值是12. 如图,直线 与双曲线 交于点A , B . 过点A作 轴,垂足为点P , 连接 .若B的坐标为 ,则 .
 13. 如图所示,一般书本的纸张是原纸张多次对开得到,矩形 沿 对开后,再把矩形 沿 对开,依次类推,若各种开本的矩形都相似,那么 的值为 .
13. 如图所示,一般书本的纸张是原纸张多次对开得到,矩形 沿 对开后,再把矩形 沿 对开,依次类推,若各种开本的矩形都相似,那么 的值为 . 14. 如图,在等边 中, ,点P为 边上一动点,M为 的中点,连接 .
14. 如图,在等边 中, ,点P为 边上一动点,M为 的中点,连接 . (1)、当点P为 的中点, 的长为;(2)、若点P移动到使 时, 的长为 .
(1)、当点P为 的中点, 的长为;(2)、若点P移动到使 时, 的长为 .三、解答题
-
15. 已知抛物线 过点 .(1)、求a的值;(2)、求该抛物线顶点的坐标.16. 已知实数x、y、z满足 ,试求 的值.17. 如图,在 中,DE∥BC , EF∥AB , .求 长及四边形 的周长.
 18. 如图,抛物线 交x轴于 、 两点,与y轴交于点C , 顶点为D .
18. 如图,抛物线 交x轴于 、 两点,与y轴交于点C , 顶点为D . (1)、求出该抛物线的解析式及顶点D的坐标.(2)、若直线 的解析式 ,请直接写出不等式 的解集.19. 如图是由边长为1的小正方形组成的网格,A、B、C、D四点均在正方形网格的格点上,线段 相交于点E .
(1)、求出该抛物线的解析式及顶点D的坐标.(2)、若直线 的解析式 ,请直接写出不等式 的解集.19. 如图是由边长为1的小正方形组成的网格,A、B、C、D四点均在正方形网格的格点上,线段 相交于点E . (1)、请在网格图中画两条线段(不添加另外的字母),构成一对相似三角形,并用“ ”符号写出这对相似三角形;(2)、求线段 的长.20. 如图所示,直线 交坐标轴于A , B两点,与反比例函数 交于点C , 过点C作x轴的垂线,垂足为D . 若 ,求k的值.
(1)、请在网格图中画两条线段(不添加另外的字母),构成一对相似三角形,并用“ ”符号写出这对相似三角形;(2)、求线段 的长.20. 如图所示,直线 交坐标轴于A , B两点,与反比例函数 交于点C , 过点C作x轴的垂线,垂足为D . 若 ,求k的值.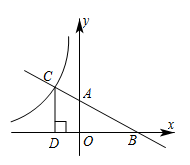 21. 小明毕业后在某水果超市做销售员,他发现一种进价为每箱40元的水果,按每箱50元出售,一个月可售出500箱,若售价每涨价1元,月销售量就会减少10箱.(1)、直接写出月销售量为y(箱)与售价x(元箱)之间的函数关系式;(2)、求月销售利润为w(元)与售价x(元箱)之间的函数关系式,并确定售价为每箱多少元时,会获得最大利润,最大利润是多少?(销售利润=销售总额-成本总额)
21. 小明毕业后在某水果超市做销售员,他发现一种进价为每箱40元的水果,按每箱50元出售,一个月可售出500箱,若售价每涨价1元,月销售量就会减少10箱.(1)、直接写出月销售量为y(箱)与售价x(元箱)之间的函数关系式;(2)、求月销售利润为w(元)与售价x(元箱)之间的函数关系式,并确定售价为每箱多少元时,会获得最大利润,最大利润是多少?(销售利润=销售总额-成本总额)
