山东省烟台市芝罘区（五四制）2021-2022学年七年级上学期期中考试数学试题

试卷更新日期：2021-12-01 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下图所示的图形分割成两个全等的图形，正确的是（　　）

A、 B、 C、 D、

查看试题解析
3. 已知三角形的两边长分别是4cm和10cm，则下列长度的线段中能作为第三边的是（）

A、4cm B、6cm C、8cm D、14cm

查看试题解析
4. 已知，△ABC≌△DEF， ∠A= 80°， ∠B=60°，则∠F 的度数是（）

A、30° B、40° C、70° D、80°

查看试题解析
5. 下列语句不能判定 $△ A B C$ 是直角三角形的是（）

A、 $a^{2} + b^{2} - c^{2} = 0$ B、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$ C、 $a ： b ： c = 3 ： 4 ： 5$ D、 $∠ A + ∠ B = ∠ C$

查看试题解析
6. 如图所示，AB＝AD ，添加下列哪个条件仍无法判定△ABC≌△ADE（）

A、∠C＝∠E B、BE＝DC C、∠CBE＝∠EDC D、BC＝DE

查看试题解析
7. 如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，若∠EFB=65°，则∠AED′等于（）

A、50° B、55° C、60° D、65°

查看试题解析
8. 如图是一个外轮廓为矩形的机器零件平面示意图，根据图中的尺寸（单位： $mm$ ），计算两圆孔中心A和B的距离为（）

A、 $80 mm$ B、 $100 mm$ C、 $120 mm$ D、 $150 mm$

查看试题解析
9. 如图，在△ABC中，已知D ， E ， F分别是BC ， AD ， CE的中点，若△ABC的面积为 $16 {cm}^{2}$ ，则△BEF（阴影部分）的面积是（）

A、2 ${cm}^{2}$ B、4 ${cm}^{2}$ C、6 ${cm}^{2}$ D、8 ${cm}^{2}$

查看试题解析
10. 某校“光学节”的纪念品是一个底面为等边三角形的三棱镜（如图），在三棱镜的侧面上，从顶点A到顶点A′镶有一圈金属丝，已知此三棱镜的高为9cm，底面边长为4cm，则这圈金属丝的长度至少为（）

A、8cm B、10cm C、12cm D、15cm

查看试题解析
11. 如图所示的网格由边长相同的小正方形组成，点 $A$ 、 $B$ 、 $C$ 、 $D$ 、 $E$ 、 $F$ 、 $G$ 在小正方形的顶点上，则 $△ A B C$ 的三条边中线的交点是（）

A、点 $D$ B、点 $E$ C、点 $F$ D、点 $G$

查看试题解析
12. 如图，AC＝BC ， ∠ACB＝90°，AE平分∠BAC交BC于点D ， BF⊥AE ，交AC的延长线于点F ，且垂足为E ，则下列结论①AD＝BF；②BF＝AF；③AC+CD＝AB；④AB＝BF：⑤AD＝2BE ．其中正确的结论有（　　）个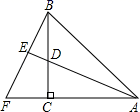

A、5 B、4 C、3 D、2

查看试题解析

二、填空题

13. 已知等腰三角形的两边长分别为1和4，则第三边长为．

查看试题解析
14. 如图，△ABC≌△DFE ，点B、E、C、F在同一直线上，BE＝2cm ， BF＝11cm ，则EC的长度是．

查看试题解析
15. 如图，小华将升旗的绳子拉到竖直旗杆的底端，绳子末端刚好接触地面，此时绳子末端距离地面2m，则绳子的总长度为 m．

查看试题解析
16. 如图，△ABC中，AB＝8cm，BC＝5cm，AC＝6cm，沿过点B的直线折叠三角形，使点C落在AB边上的点E处，折痕为BD ，则△AED的周长长度为．

查看试题解析
17. 国庆假期中，小华与同学去玩探宝游戏，按照探宝图，他们从门口A处出发先往东走8km，又往北走2km，遇到障碍后又往西走3km，再向北走到6km处往东拐，仅走了1km，就找到了宝藏，则门口A到藏宝点B的直线距离是．

查看试题解析
18. 如图，△ABC的角平分线BD与CE交于点O ，若∠COD＝50°，则∠BAC的度数是．

查看试题解析
19. 如图，△ABC中，∠ACB＝90°，∠B＝30°，AD平分∠CAB交BC于点D ，若BC＝9cm，则CD的长度是．

查看试题解析
20. 如图，点P为∠AOB内一点，点M、N分别是边OA和OB上的动点，且M、P、N不共线，若∠AOB＝30°，OP＝8cm ，则△PMN周长的最小值是．

查看试题解析

三、解答题

21. 如图，已知△ABC ，求作：△OMN ，使∠MON＝∠ABC ， OM＝BC ， MN＝AC ．（保留作图痕迹，不必写作法）

查看试题解析
22. 如图，在△ABC中，CD⊥AB于点D ， AC＝20，CB＝15，BD＝9，求AD与△ABC的面积．

查看试题解析
23. 如图为10×10的正方形网格，每个小正方形的边长均为1，小正方形的顶点叫做格点，顶点在格点上的三角形叫做格点三角形．已知△ABC是格点三角形，
按要求解决下列问题：

(1)、请直接写出△ABC的面积；

(2)、①以AC为一边，在AC的下方画一个格点△ACD ，使它与△ABC成轴对称，并画出对称轴m；
②以点B为顶点画一个格点△BEF ，使它与△ABC全等且仅有一个公共顶点B ．

查看试题解析
24. 如图， $△ A B C$ 和 $△ E F D$ 的边BC、DF在同一直线上（D点在C点的左边），已知 $∠ A = ∠ E$ ， $A B // E F$ ， $B D = C F$ ．

(1)、求证： $△ A B C ≌ △ E F D$ ．

(2)、求证： $A C // D E$ ．

查看试题解析
25. 如图，在△ABC中，∠ACB＝90°，AC＝BC ， AD⊥CE ， BE⊥CE ，垂足分别为D、E

(1)、求证：CD＝BE

(2)、若AD＝3.5 cm，DE＝2.7 cm，求BE的长

查看试题解析
26. 台风是一种自然灾害，它以台风中心为圆心在周围上千米的范围内形成极端气候，有极强的破坏力，有一台风中心沿东西方向AB由点A行驶向点B，已知点C为一海港，且点C与直线AB上两点A、B的距离分别为300km和400km，又AB＝500km，以台风中心为圆心周围250km以内为受影响区域．

(1)、海港C会受台风影响吗？为什么？

(2)、若台风的速度为20km/h，台风影响该海港持续的时间有多长？

查看试题解析
27. 如图，已知△ABC与△DEC都是等腰三角形，∠ACB＝∠DCE＝90°．

(1)、试说明：△ACD≌△BCE；

(2)、若AC＝6，AE＝3，∠CAE＝45°，求AD的长．

查看试题解析