山东省临沂市蒙阴县2021-2022学年七年级上学期期中数学试题

试卷更新日期：2021-12-01 类型：期中考试

进入出卷网下载

一、单选题

1. 据统计，国家“一带一路”倡议将产生 $21000000000000$ 美元的经济效益，数据 $21000000000000$ 用科学记数法可表示为（）

A、 $21 \times 10^{12}$ B、 $2.1 \times 10^{12}$ C、 $2.1 \times 10^{13}$ D、 $0.21 \times 10^{14}$

查看试题解析
2. 一种风筝牌面粉的质量标识为“ $50 \pm 0.25$ 千克”，则下列面粉中合格的有（）

A、 $49.70$ 千克 B、 $50.32$ 千克 C、 $50.51$ 千克 D、 $49.86$ 千克

查看试题解析
3. 据统计，国家“一带一路”倡议将产生 $21000000000000$ 美元的经济效益，数据 $21000000000000$ 用科学记数法可表示为（）

A、 $21 \times 10^{12}$ B、 $2.1 \times 10^{12}$ C、 $2.1 \times 10^{13}$ D、 $0.21 \times 10^{14}$

查看试题解析
4. 若 $- (- 3)$ 表示一个数的相反数，则这个数是（）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、 $3$ D、 $- 3$

查看试题解析
5. 若 $- (- 3)$ 表示一个数的相反数，则这个数是（）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、 $3$ D、 $- 3$

查看试题解析
6. 有理数 ${(- 1)}^{2}$ ， ${(- 1)}^{3}$ ， $- 1^{2}$ ， $| - 1 |$ ， $- (- 1)$ ， $\frac{1}{- 1}$ 中，其中等于 $1$ 的个数是（）

A、 $3$ 个 B、 $4$ 个 C、 $5$ 个 D、 $6$ 个

查看试题解析
7. 下列结论中，正确的是（）．

A、单项式 $\frac{3 x y^{2}}{7}$ 的系数是3，次数是2 B、单项式 $m$ 的次数是1，没有系数 C、单项式 $- x y^{2} z$ 的系数是-1，次数是4 D、多项式 $2 x^{2} + x y + 3$ 是三次三项式

查看试题解析
8. 下列计算正确的是（）

A、 $4 a - 2 a = 2$ B、 $4 a^{2} + a = 5 a^{2}$ C、 $- a^{3} - a^{3} = - 2 a^{3}$ D、 $2 a^{2} - a = a$

查看试题解析
9. 若多项式 $x^{2} + (5 + a) x - 2$ 中不含x的一次项，则a的值为（）

A、 $0$ B、 $5$ C、 $- 5$ D、 $5$ 或 $- 5$

查看试题解析
10. 下列各式去括号正确的是（）

A、 $a^{2} - (2 a - b + c) = a^{2} - 2 a - b + c$ B、 $- (x - y) + (x y - 1) = - x - y + x y - 1$ C、 $a - (3 b - 2 c) = a - 3 b - 2 c$ D、 $9 y^{2} - [x - (5 z + 4)] = 9 y^{2} - x + 5 z + 4$

查看试题解析
11. 将 $1$ ， $- 1$ ， $- 5$ ， $2$ 这四个数分别用点表示在数轴上，其中与 $- 2$ 所表示的点最近的数是（）

A、 $1$ B、 $- 1$ C、 $- 5$ D、 $2$

查看试题解析
12. 如果 $- x y^{b - 1}$ 与 $\frac{1}{2} x^{a + 2} y^{4}$ 的和是单项式，那么 $a^{b} =$ （）

A、 $- 1$ B、 $1$ C、 $0$ D、 $- 2$

查看试题解析
13. 已知数a、b、c在数轴上的位置如图所示，化简|a+b|﹣|c﹣b|的结果是（）

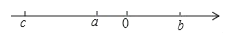A、a+b B、﹣a﹣c C、a+c D、a+2b﹣c

查看试题解析
14. 已知代数式x+2y+1的值是3，则代数式2x+4y+1的值是（）

A、4 B、5 C、7 D、不能确定

查看试题解析
15. 有12米长的木条，要做成一个如图的窗框，如果假设窗框横档的长度为x米，那么窗框的面积是（木条的宽度忽略不计）（）

A、 $x (6 - \frac{3}{2} x) m^{2}$ B、 $x (12 ﹣ x)$ $m^{2}$ C、 $x (6 ﹣ 3 x)$ $m^{2}$ D、 $x (6 ﹣ x)$ $m^{2}$

查看试题解析
16.
观察下面“品”字形中各数之间的规律，根据观察到的规律得出a的值为（）

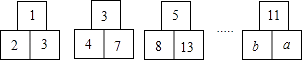A、23 B、75 C、77 D、139

查看试题解析

二、填空题

17. 如果 $| m | = | - 6 |$ ，那么 $m =$ ．

查看试题解析
18. 已知a、b互为相反数，c、d互为倒数，那么 $a + b - 5 c d =$ ．

查看试题解析
19. 若 $| b - 2 | + {(a + 3)}^{2} = 0$ ，则 ${(a + b)}^{2019}$ 的值为．

查看试题解析
20. 按图中计算程序计算，若开始输入的值为-2，则最后输出的结果是．

查看试题解析
21. 《庄子．天下篇》中写道：“一尺之棰，日取其半，万世不竭”意思是：一根一尺的木棍，如果每天截取它的一半，永远也取不完，如图．

由图易得： $\frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + \dots + \frac{1}{2^{n}}$ = ．

查看试题解析

三、解答题

22. 计算

(1)、 $4 \frac{3}{4} - (+ 3.85) - (- 3 \frac{1}{4}) + (- 3.15)$

(2)、 $- 3^{2} - [{(- 2)}^{2} - (1 - \frac{4}{5} \times \frac{3}{4}) \div (- 2)]$

查看试题解析
23. 我们定义一种新运算： $x * y = x^{2} y + x - y$ ．

(1)、求 $2 * (- 4)$ 的值；

(2)、求 $(- 1) * [4 * (- 2)]$ 的值．

查看试题解析
24.

(1)、先化简，再求值： $- 2 (x^{2} - 3 y) - [x^{2} - 3 (2 x^{2} - 3 y)]$ ，其中 $x = - 1$ ， $y = - 2$ ．

(2)、已知多项式A，B，其中 $A = x^{2} - 2 x + 1$ ，小马在计算 $A + B$ 时，由于粗心把 $A + B$ 看成 $A - B$ ，求得结果为 $- 3 x^{2} - 2 x - 1$ ，请你帮小马算出 $A + B$ 的符合题意结果．

查看试题解析

25. 蒙阴县的蜜桃闻名全国，现有

20

筐蜜桃，以每筐

23

千克为标准，超过或不足的千克数分别用正数或负数来表示，记录如下：

(1)、与标准重量比较，

20

筐蜜桃总计超过或不足多少千克？

与标准质量的差值

（单位：千克）

$- 3$

$- 2$

$- 1.5$

$0$

$1$

$2.5$

筐数

$1$

$4$

$2$

$3$

$2$

$8$

(2)、若蜜桃每千克售价

5

元，则这

20

筐可卖多少元？

查看试题解析

26. 一辆客车从甲地开往乙地，车上原有（5a﹣2b）人，中途停车一次，有一些人下车，此时下车的人数比车上原有人数一半还多2人，同时又有一些上车，上车的人数比 $\frac{1}{2}$ （7a﹣4b）少3人．

(1)、用代数式表示中途下车的人数；

(2)、用代数式表示中途下车、上车之后，车上现在共有多少人？

(3)、当a=10，b=9时，求中途下车、上车之后，车上现在的人数？

查看试题解析
27. 观察下列等式：
$\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ，

将以上三个等式两边分别相加得：

$\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} = 1 - \frac{1}{4} = \frac{3}{4}$

(1)、猜想并写出 $\frac{1}{n (n + 1)} =$ ．

(2)、直接写出下列各式的计算结果：
$\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{2015 \times 2016} =$ ；

(3)、探究并解决问题：
试求： $\frac{1}{2 \times 4} + \frac{1}{4 \times 6} + \frac{1}{6 \times 8} + \dots + \frac{1}{2014 \times 2016}$

查看试题解析
28. 阅读材料：我们知道， $4 x - 2 x + x = (4 - 2 + 1) x = 3 x$ ，类似地，我们把 $(a + b)$ 看成一个整体，则 $4 (a + b) - 2 (a + b) + (a + b) = (4 - 2 + 1) (a + b) = 3 (a + b)$ ，“整体思想”是中学教学课题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．

(1)、尝试应用：把 ${(a - b)}^{2}$ 看成一个整体，合并 $3 {(a - b)}^{2} - 5 {(a - b)}^{2} + 7 {(a - b)}^{2}$ 的结果是．

(2)、已知 $2 x^{2} - 3 y = 6$ ，求 $- 4 x^{2} + 6 y - 5$ 的值．

(3)、拓展探索：
已知 $a - 2 b = 2$ ， $2 b - c = - 5$ ， $c - d = 9$ ，求 $(2 a - c) + (2 b - 3 d) - (4 b - 3 c)$ 的值．

查看试题解析