山东省济宁市金乡县2021-2022学年七年级上学期期中数学试题

试卷更新日期：2021-12-01 类型：期中考试

进入出卷网下载

一、单选题

1. 计算： $(- 3) \times 5$ 的结果是（）

A、15 B、2 C、 $- 2$ D、 $- 15$

查看试题解析
2. 下列各数中比-2小的数是（）

A、 $- 3$ B、 $- 1$ C、 $0$ D、 $2$

查看试题解析
3. 单项式-5ab的系数是（）

A、5 B、 $- 5$ C、2 D、 $- 2$

查看试题解析
4. 计算 $2 a - 3 a$ ，结果正确的是（　　）

A、﹣1 B、1 C、﹣a D、a

查看试题解析
5. 用四舍五入法，把数4.803精确到百分位，得到的近似数是（）

A、4.8 B、4.80 C、4.803 D、5.0

查看试题解析
6. 下列选项中，说法正确的是（）

A、 $3^{2} a b^{3}$ 的次数是6次 B、 $x + \frac{1}{x}$ 不是多项式 C、 $x^{2} + x - 1$ 的常数项为1 D、多项式 $2 x^{2} + x y + 3$ 是四次三项式

查看试题解析
7. 下列各式正确的是（）

A、 $- | - 5 | = 5$ B、 $- (- 5) = - 5$ C、 $| - 5 | = - 5$ D、 $- (- 5) = 5$

查看试题解析
8. 若 $2 a^{2} - 3 b = - 1$ ，则代数式 $4 a^{2} - 6 b + 3$ 的值为（）

A、1 B、2 C、3 D、4

查看试题解析
9. 某商店在甲批发市场以每包a元的价格进了40包茶叶，又在乙批发市场以每包b元（a＜b）的价格进了同样的60包茶叶，如果以每包 $\frac{a + b}{2}$ 元的价格全部卖出这种茶叶，那么这家商店盈利还是亏损（）

A、盈利了 B、亏损了 C、不盈不亏 D、盈亏不能确定

查看试题解析
10. 观察下列等式： $7^{0} = 1$ ， $7^{1} = 7$ ， $7^{2} = 49$ ， $7^{3} = 343$ ， $7^{4} = 2401$ ， $7^{5} = 16807$ ，…根据其中的规律可得 $7^{0} + 7^{1} + \dots + 7^{2022}$ 的结果的个位数字是（）

A、0 B、1 C、7 D、8

查看试题解析

二、填空题

11. 单项式 $\frac{1}{2} a^{3} b^{2}$ 的次数是．

查看试题解析
12. $| - 1.5 |$ 的倒数是．

查看试题解析
13. 预计到2025年，中国5G用户将超过460 000 000，将460 000 000用科学记数法表示为.

查看试题解析
14. 已知： $[x]$ 表示不超过 $x$ 的最大整数．例： $[4.8] = 4$ ， $[- 0.8] = - 1$ ．现定义： ${x} = x - [x]$ ，例： ${1.5} = 1.5 - [1.5] = 0.5$ ，则 ${3.9} + {- 1.8} - {1} =$ ．

查看试题解析
15. 观察下列关于x的单项式：x ， $3 x^{2}$ ， $5 x^{3}$ ， $7 x^{4}$ ， $9 x^{5}$ ， $11 x^{6}$ ，…，按照上述规律，第2021个单项式是．

查看试题解析

三、解答题

16. 计算：

(1)、 $- 108 - (- 112) + 23 + 18$

(2)、 ${(- 2)}^{4} \div (- 8) - {(- \frac{1}{2})}^{3} \times (- 2^{2})$

查看试题解析
17. 化简：

(1)、 $a^{2} b - (4 a b + 3 a^{2} b) + a b$

(2)、 $x y - [x^{2} - (3 x y - y^{2} - 2 x^{2})] - 2 y^{2}$

查看试题解析
18. 已知关于a ， b的单项式 $\frac{2}{5} a^{m + n} b^{2}$ 与单项式 $- a^{6} b^{m + 1}$ 是同类项．

(1)、求m ， n的值；

(2)、求整式 $3 (m^{2} - 2 m n + n^{2}) - [4 m^{2} - 2 (\frac{1}{2} m^{2} + m n - \frac{3}{2} n^{2})]$ 的值．

查看试题解析
19. 小明在计算减多项式A减 $2 b^{2} - 3 b - 5$ 时，因一时疏忽忘了将两个多项式用括号括起来，得到的结果是 $b^{2} + 3 b - 1$ ．

(1)、求这个多项式A ．

(2)、求这两个多项式相减的符合题意结果．

(3)、当 $b = - 1$ 时，求（2）中结果的值．

查看试题解析
20. 为了绿化校园，学校决定修建一块长方形草坪，长 $30$ 米，宽 $20$ 米，并在草坪上修建如图所示的等宽的十字路，小路宽为 $x$ 米

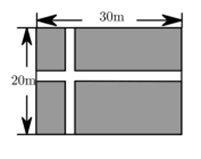(1)、用代数式表示草坪的面积是多少平方米

(2)、当 $x = 3$ 米时，求草坪的面积

查看试题解析
21. 设 $a > 0$ ，x，y为有理数，定义新运算： $a ※ x = a \times | x |$ ．如 $3 ※ 2 = 3 \times | 2 | = 6$ ， $4 ※ (a - 1) = 4 \times | a - 1 |$ ．

(1)、计算 $2021 ※ 0$ 和 $2021 ※ (- 2)$ 的值．

(2)、若 $y < 0$ ，化简 $2 ※ (- 3 y)$ ．

(3)、请直接写出一组 $a ， x ， y$ 的具体值，说明 $a ※ (x + y) = a ※ x + a ※ y$ 不成立．

查看试题解析
22. 我们知道：在研究和解决数学问题时，当问题所给对象不能进行统一研究时，我们就需要根据数学对象的本质属性的相同点和不同点，将对象区分为不同种类，然后逐类进行研究和解决，最后综合各类结果得到整个问题的解决，这一思想方法，我们称之为“分类讨论的思想”这一数学思想用处非常广泛，我们经常用这种方法解决问题．例如：我们在讨论|a|的值时，就会对a进行分类讨论，当a≥0时，|a|＝a；当a＜0时，|a|＝﹣a ．现在请你利用这一思想解决下列问题：

(1)、 $\frac{8}{| 8 |} =$ ； $\frac{- 3}{| - 3 |} =$ ；

(2)、 $\frac{a}{| a |} =$ （a≠0）， $\frac{a}{| a |} + \frac{b}{| b |} =$ （其中a＞0，b≠0）；

(3)、若abc≠0，试求 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |} + \frac{a b c}{| a b c |}$ 的所有可能的值．

查看试题解析