安徽省合肥市长丰县2021-2022学年七年级上学期期中数学试题

试卷更新日期：2021-12-01 类型：期中考试

进入出卷网下载

一、单选题

1. $- \frac{1}{2}$ 的绝对值是（）

A、2 B、 $- 2$ C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 在有理数1，- $\frac{1}{5}$ ， $\frac{1}{3}$ ，-3中，倒数最小的是（）

A、1 B、- $\frac{1}{5}$ C、 $\frac{1}{3}$ D、-3

查看试题解析
3. 美妙的音乐能陶冶情操，催人奋进．根据下面五线谱中的信息，确定最后一个音符(“?” 处)的时值长应为（）

A、 $\frac{3}{4}$ B、 $\frac{1}{4}$ C、 $\frac{1}{8}$ D、 $\frac{1}{2}$

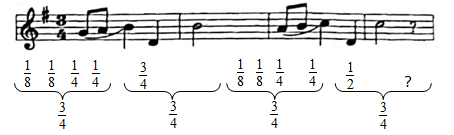查看试题解析
4. 接种新冠疫苗，共建防疫屏障．根据安徽省免疫规划信息系统最新统计，截至2021年8月18日13时，安徽省累计接种新冠病毒疫苗超过8000万剂次，其中8000万用科学记数法表示为（）

A、8×10³ B、8×10⁷ C、8×10⁵ D、8×10⁶

查看试题解析
5. 化简-3(a-b) ，结果正确的是（）

A、-3a-b B、-3a+b C、-3a+3b D、-3a-3b

查看试题解析
6. 多项式 $\frac{3}{4} x^{2} + \frac{2}{5} x y^{2} - 10 x$ 的各项系数之积是（）

A、 $\frac{3}{10}$ B、- $\frac{3}{10}$ C、3 D、-3

查看试题解析
7. 在解关于x的方程 $\frac{2 x -1}{3} = \frac{x + a}{2} - 2$ 时，小冉在去分母的过程中，右边的“-2”漏乘了公分母6，因而求得方程的解为x=2，则方程正确的解是（）

A、x=-12 B、x=-8 C、x=8 D、x=12

查看试题解析
8. 某地区居民生活用水收费标准：每月用水量不超过15立方米，每立方米a元；超过15立方米的部分每立方米(a+1.2)元，若该地区某用户上月用水量为20立方米，则应缴水费（）

A、20a元 B、(20a +24)元 C、(20a+6)元 D、(20a+3.6)元

查看试题解析
9. 已知等式3a＝2b+5，则下列等式变形错误的是（　　）

A、3a﹣5＝2b B、3a+1＝2b+6 C、a＝ $\frac{2}{3}$ b+ $\frac{5}{3}$ D、3ac＝2bc+5

查看试题解析
10. 如图，数轴上的点A所表示的有理数为a ，化简|a|-|a+2|的结果为（）

A、-2a-2 B、-2 C、2a+ 2 D、2

查看试题解析

二、填空题

11. 若-5x²y^m与2xⁿy³是同类项，则m+n的值为．

查看试题解析
12. 若2ⁿ-1=5，则4×2ⁿ-4= ．

查看试题解析
13. 幻方历史悠久，传说最早出现在夏禹时代的“洛书”当中．把洛书用今天的数学符号翻译出来，就是一个三阶幻方．将数字1～9分别填入如图所示的幻方中，要求每一横行，每一竖行以及两条对角线上的数字之和都是15，则m的值为．

查看试题解析
14. 在某学校“庆祝中国共产党建党100周年”的活动上，小青同学用围棋棋子按照某种规律摆成如图所示的“100”字样．

(1)、观察图案，图6有个棋子．

(2)、按照这种规律，第n个“100”字样图案的棋子个数是(用含 n的代数式表示)．

查看试题解析

三、解答题

15.

(1)、化简：x-5x+6x ．

(2)、计算： $(\frac{1}{4} + \frac{1}{6} - \frac{1}{3}) \times 12$

查看试题解析
16. 解方程：4x+1=2(x-1)+6．

查看试题解析
17. 已知|a|=2，|b|=1，且b＞a ，求2a-3b的值；

查看试题解析
18. 合肥市某新能源汽车工厂的一个生产车间有两条生产线，第一条生产线有20人，第二条生产线有25人，根据市场需求情况，在总人数不变的情况下，要将第二条生产线的人数调整为第一条生产线人数的一半，问应从第二条生产线调多少人到第一条生产线？

查看试题解析
19. 先化简，再求值：5a²-[a²-（2a-5a²）-2（a²-3a）]，其中a=4

查看试题解析

20. 观察表格中两个多项式及其相应的值，回答问题：

x	…	$- 2$	$- 1$	0	1	2	…
$- 2 x + 4$	…	8	6	4	2	a	…
$3 x - 5$	…	$- 11$	$- 8$	$- 5$	$- 2$	b	…

(1)、（初步感知）

根据表中信息可知： $a =$ ； $b =$ ．

(2)、（归纳规律）

表中 $- 2 x + 4$ 的值的变化规律：x的值每增加1， $- 2 x + 4$ 的值就减少2．类似地， $3 x - 5$ 的值的变化规律：．

(3)、（问题解决）

请直接写出一个含x的多项式，要求x的值每增加1，多项式的值就减小5，且当 $x = 0$ 时，多项式的值为6．

查看试题解析

21. 某仓库在一周的货品运输中，进出情况如下表所示（进库为正，出库为负，单位：吨）：

星期一	星期二	星期三	星期四	星期五	星期六	星期日	合计
$+ 26$	$- 16$	$+ 42$	$- 30$		$- 25$	$- 9$	$+ 8$

表中星期五的进出数被墨水涂污了

(1)、请你算出星期五仓库的进出数．

(2)、如果仓库进出的装卸费都是每吨50元，那么这一周要付多少元装卸费？

查看试题解析

22. 李老师写出了一个整式（ax²+bx-2）-（5x²+3x），其中a、b为常数，且表示为系数，然后让同学赋予a、b不同的数值进行计算．

(1)、甲同学给出了a=6、b=-2，请按照甲同学给出的数值化简整式；

(2)、乙同学给出了一组数据，最后计算的结果为3x²-2x-2，求乙同学给出的a、b的值；

(3)、丙同学给出了一组数据，计算的最后结果与x的取值无关，请求出丙同学的计算结果；

查看试题解析
23. 如图，数轴上A、B两点对应的数分别为-2、5，P为数轴上一动点，其对应的数为m ．

(1)、若点P到A、B两点的距离都相等，请直接写出点P对应的数m的值；

(2)、数轴上是否存在点P ，使点P到点A ，点B的距离之和为10个单位长度?若存在，求出点P所表示的数；

(3)、点A、B分别以2个单位长度/分，1个单位长度/分的速度向右运动，同时点P以每分钟5个单位长度的速度从O点向左运动，当遇到点A时，点P以原来的速度向右运动，并不停地往返于点A与点B之间，求当点A与点B重合时，点P所经过的总路程．

查看试题解析