北京市海淀区2021-2022学年高二上学期数学期中考试试卷
试卷更新日期:2021-12-01 类型:期中考试
一、单选题
-
1. 长方体 中,化简 ( )A、 B、 C、 D、2. 已知 , ,若 ,则实数 , 的值分别为( )A、 , B、 , C、5,2 D、-5,-23. 过点 且与向量 垂直的向量( )A、有且只有一个 B、有无数个且共面 C、只有两个且方向相反 D、有无数个且共线4. 若直线 的方向向量为 ,平面 的法向量为 ,则能使 的是( )A、 , B、 , C、 , D、 ,5. 若平面 的法向量为 ,直线 的方向向量为 ,直线 与平面 的夹角为 ,则下列关系式成立的是( )A、 B、 C、 D、6. 已知空间直角坐标系 中的点 关于 平面的对称点为 ,则 为( )A、2 B、4 C、6 D、以上都不对7. 埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
 A、 B、 C、 D、8. 已知 , 是两条不同直线, , 是两个不同平面,则下列命题正确的是( )A、若 , 垂直于同一平面,则 与 平行 B、若 , 平行于平面 ,则 与 平行 C、若 , 不平行,则 与 不可能垂直于同一平面 D、若 , 不平行,则在 内不存在与 平行的直线9. 如图已知正方体 ,M , N分别是 , 的中点,则( )
A、 B、 C、 D、8. 已知 , 是两条不同直线, , 是两个不同平面,则下列命题正确的是( )A、若 , 垂直于同一平面,则 与 平行 B、若 , 平行于平面 ,则 与 平行 C、若 , 不平行,则 与 不可能垂直于同一平面 D、若 , 不平行,则在 内不存在与 平行的直线9. 如图已知正方体 ,M , N分别是 , 的中点,则( )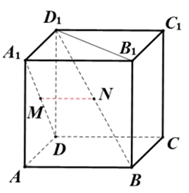 A、直线 与直线 垂直,直线 平面 B、直线 与直线 平行,直线 平面 C、直线 与直线 相交,直线 平面 D、直线 与直线 异面,直线 平面10. 已知正方体的棱长为1,每条棱所在直线与平面 所成的角都相等,则 截此正方体所得截面面积的最大值为( )A、 B、 C、 D、
A、直线 与直线 垂直,直线 平面 B、直线 与直线 平行,直线 平面 C、直线 与直线 相交,直线 平面 D、直线 与直线 异面,直线 平面10. 已知正方体的棱长为1,每条棱所在直线与平面 所成的角都相等,则 截此正方体所得截面面积的最大值为( )A、 B、 C、 D、二、填空题
-
11. 已知长方体从同一顶点出发的三条棱的长分别为1、2、3,则这个长方体的外接球的表面积为.12. 半径为 的半圆卷成一个圆锥,则它的体积为 .13. 平面 的法向量为 ,若向量 ,则直线 与平面 的位置关系为 .14. 已知 , ,则以 , 为邻边的平行四边形的面积为.15. 正四棱锥的底面边长为4,侧棱长为3,则侧面与底面所成二面角的余弦值为 .16. 已知关于向量的命题,
⑴ 是 , 共线的充分不必要条件;
⑵若 ,则存在唯一的实数 ,使 ;
⑶ , ,则 ;
⑷若 为空间的一个基底,则 构成空间的另一基底;
⑸ .
在以上命题中,所有正确命题的序号是 .
三、解答题
-
17. 正四棱柱 中, , , 为 中点, 为下底面正方形的中心.求:
 (1)、异面直线 与 所成角的余弦值;(2)、二面角 的余弦值;(3)、点 到平面 的距离.
(1)、异面直线 与 所成角的余弦值;(2)、二面角 的余弦值;(3)、点 到平面 的距离.

