山东省济南市长清三中2021-2022学年九年级上学期第一次月考数学试题

试卷更新日期：2021-11-30 类型：月考试卷

进入出卷网下载

一、单选题

1. 若 $3 a = 2 b$ ，则 $\frac{a}{b}$ 的值为（）

A、 $\frac{5}{3}$ B、 $\frac{5}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{2}$

查看试题解析
2. 同时抛掷两枚均匀的硬币，落地后两枚硬币都是正面朝上的概率是（）

A、 $1$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
3. 方程x（x+1）＝0的解是（）

A、x＝0 B、x＝1 C、x₁＝0，x₂＝1 D、x₁＝0，x₂＝﹣1

查看试题解析
4. 已知四条线段的长如下，则能成比例线段的是（）

A、1，1，2，3 B、1，2，3，4 C、1，2，2，4 D、2，3，4，5

查看试题解析
5. 在一个不透明的袋子中有除颜色外均相同的6个白球和若干黑球，通过多次摸球试验后，发现摸到白球的频率约为30%，估计袋中黑球有（）个．

A、8 B、9 C、14 D、15

查看试题解析
6. 把方程x²﹣10x﹣5＝0变形为（x+h）²＝k的形式可以是（）

A、（x﹣5）²＝30 B、（x﹣5）²＝5 C、（x+5）²＝5 D、（x+5）²＝30

查看试题解析
7. 如图，是某射手在相同条件下进行射击训练的结果统计图，该射手击中靶心的概率的估计值为（）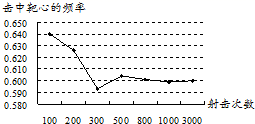

A、0.600 B、0.640 C、0.595 D、0.605

查看试题解析
8. 若 $\frac{a}{b} = \frac{d}{c}$ ，则下列比例式中错误的是（）

A、 $\frac{a}{d} = \frac{b}{c}$ B、 $\frac{d}{a} = \frac{c}{b}$ C、 $\frac{a}{c} = \frac{b}{d}$ D、 $\frac{b}{a} = \frac{c}{d}$

查看试题解析
9. 某学校组织学生到社区开展公益宣传活动，成立了“垃圾分类”“文明出行”“低碳环保”三个宣传队，如果小华和小丽每人随机选择参加其中一个宣传队，则她们恰好选到同一个宣传队的概率是（）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{2}{3}$

查看试题解析
10. 若关于x的一元二次方程x²－2x＋k=0有两个不相等的实数根，则k的取值范围是（）

A、k<1 B、k≤1 C、k>－1 D、k>1

查看试题解析
11. 关于x的方程ax²﹣2x﹣1＝0有实数根，则a的取值范围是（）

A、a≥﹣1 B、a＞﹣1 C、a≥﹣1且a≠0 D、a＞﹣1且a≠0

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ A B C = 90 ° ， A B = 8 cm ， B C = 6 cm$ ，动点P，Q分别从点A，B同时开始移动（移动方向如图所示），点P的速度为 $1cm/s$ ，点Q的速度为 $2cm/s$ ，点Q移动到C点后停止，点P也随之停止运动，当 $△ P B Q$ 的面积为 ${15cm}^{2}$ 时，则点P运动的时间是（）

A、 $3s$ B、 $3s$ 或 $5s$ C、 $4s$ D、 $5s$

查看试题解析

二、填空题

13. 已知 $\frac{a}{b} = \frac{5}{2}$ ，则 $\frac{a - b}{b} =$ .

查看试题解析
14. 如图，在两个同心圆中，四条直径把大圆分成八等份，若往圆面投掷飞镖，则飞镖落在黑色区域的概率是．

查看试题解析
15. 关于 $x$ 的一元二次方程 $x^{2} + x - a = 0$ 的一个根是2，则另一个根是．

查看试题解析
16. 有一只鸡患了 $H 7 N 9$ 流感，经过两轮传染后共有 $100$ 只鸡患了流感，那么每轮传染中，平均一只鸡传染的只数为．

查看试题解析
17. 如果关于x的方程（m﹣3）x^|m^﹣1|﹣x+3＝0是一元二次方程，则m＝

查看试题解析
18. 某药品经过两次降价，每瓶零售价由100元降为81元.已知两次降价的百分率相同，则每次降价的百分率是.

查看试题解析

三、解答题

19. 用适当的方法解下列方程

(1)、x²+2x﹣3＝0；

(2)、2x（x+1）＝3（x+1）．

查看试题解析
20. 已知 $a ： b ： c = 2 ： 3 ： 4$ ，且 $a + 3 b - 2 c = 15$ ，求 $a + b - c$ 的值．

查看试题解析
21. 有一块长12cm，宽8cm的长方形铁皮，如果在铁皮的四个角上截去四个相同的小正方形，然后把四边折起来，做成一个底面面积为32cm²的无盖的盒子，求截去的小正方形的边长．

查看试题解析
22. 参加一次聚会的每两人都握了一次手，所有人共握手6次，有多少人参加聚会？（列一元二次方程，解应用题）

查看试题解析
23. 一个不透明的袋子中装有红、白两种颜色的小球，这些球除颜色外完全相同，其中红球有 $1$ 个，若从中随机摸出一个球，这个球是白球的概率为 $\frac{2}{3}$ .

(1)、请直接写出袋子中白球的个数.

(2)、随机摸出一个球后，放回并搅匀，再随机摸出一个球，求两次都摸到相同颜色的小球的概率.（请结合树状图或列表解答）

查看试题解析
24. 某超市2019年盈利64万元，2021年盈利100万元．

(1)、求这两年投入教育经费的年平均增长百分率是多少？

(2)、预计2022年投入的教育经费是多少？

查看试题解析

25. 八年级一班开展了“读一本好书”的活动，班委会对学生阅读书籍的情况进行了问卷调查，问卷设置了“小说”、“戏剧”、“散文”、“其他”四个类别，每位同学仅选一项，根据调查结果绘制了不完整的频数分布表和扇形统计图．根据图表提供的信息，回答下列问题：

类别	频数（人数）	频率
小说		0.5
戏剧	4
散文	10	0.25
其他	6
合计	m	1

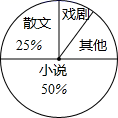(1)、计算m＝；

(2)、在扇形统计图中，“其他”类所占的百分比为；

(3)、在调查问卷中，甲、乙、丙、丁四位同学选择了“戏剧”类，现从中任意选出2名同学参加学校的戏剧社团，请用画树状图或列表的方法，求选取的2人恰好是乙和丙的概率．

查看试题解析

26. 某学校八年级共400名学生，为了解该年级学生的视力情况，

从中随机抽取40名学生的视力数据作为样本，数据统计如下：

4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2

5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2

4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1

4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3

根据数据绘制了如下的表格和统计图：

等级	视力（x）	频数	频率
A	x＜4.2	4	0.1
B	4.2≤x≤4.4	12	0.3
C	4.5≤x≤4.7	a
D	4.8≤x≤5.0		b
E	5.1≤x≤5.3	10	0.25
合计		40	1

根据上面提供的信息，回答下列问题：

(1)、统计表中的a＝， b＝；

(2)、根据抽样调查结果，请估计该校八年级学生视力为“E级”的有多少人？

(3)、该年级学生会宣传部有2名男生和2名女生，现从中随机挑选2名同学参加“防控近视，爱眼护眼”宣传活动，请用树状图法或列表法求出恰好选中“1男1女”的概率．

查看试题解析

27. 某商场销售一批衬衫，平均每天可售出20件，每件盈利40元，为扩大销售增加盈利，尽快减少库存，商场决定采取降价措施，经调查发现，若每件衬衫每降价1元，商场平均每天可以多售出2件．

(1)、若每件降价x元，每天盈利y元，求y与x的关系式．

(2)、若商场平均每天要盈利1200元，每件衬衫应降价多少元？

(3)、每件衬衫降价多少元时，商场每天盈利最多？盈利多少元？

查看试题解析