辽宁省大连市瓦房店市2021-2022学年九年级上学期第一次月考数学试题
试卷更新日期:2021-11-30 类型:月考试卷
一、单选题
-
1. 若关于x的方程ax2﹣2m﹣3=x(2﹣x)是一元二次方程,则a的取值范围是( )A、a≠0 B、a≠2 C、a≠1 D、a≠—12. 若正数a是一元二次方程x2﹣5x+m=0的一个根,﹣a是一元二次方程x2+5x﹣m=0的一个根,则a的值是( )A、 B、﹣ C、﹣5 D、53. 如图,AB∥CD,AE∥FD,AE、FD分别交BC于点G、H,则图中共有相似三角形( )
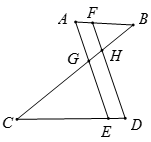 A、4对 B、5对 C、6对 D、7对4. 在△ABC中,∠C=90°,AC=6,cosA= ,则BC的长为( )A、6 B、8 C、10 D、95. 如果关于x的一元二次方程 有两个不相等的实数根,那么k的取值范围是( )A、k< B、k< 且k≠0 C、﹣ ≤k< D、﹣ ≤k< 且k≠06. sin70°,cos70°,tan70°的大小关系是( )A、tan70°<cos70°<sin70° B、cos70°<tan70°<sin70° C、sin70°<cos70°<tan70° D、cos70°<sin70°<tan70°7. 已知m,n是关于x的一元二次方程 的两个解,若 ,则a的值为( )A、﹣10 B、4 C、﹣4 D、108. 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ADC的值为( )
A、4对 B、5对 C、6对 D、7对4. 在△ABC中,∠C=90°,AC=6,cosA= ,则BC的长为( )A、6 B、8 C、10 D、95. 如果关于x的一元二次方程 有两个不相等的实数根,那么k的取值范围是( )A、k< B、k< 且k≠0 C、﹣ ≤k< D、﹣ ≤k< 且k≠06. sin70°,cos70°,tan70°的大小关系是( )A、tan70°<cos70°<sin70° B、cos70°<tan70°<sin70° C、sin70°<cos70°<tan70° D、cos70°<sin70°<tan70°7. 已知m,n是关于x的一元二次方程 的两个解,若 ,则a的值为( )A、﹣10 B、4 C、﹣4 D、108. 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ADC的值为( )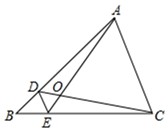 A、1:16 B、1:18 C、1:20 D、1:249. 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=4,CE= ,则△ABC的面积为( )
A、1:16 B、1:18 C、1:20 D、1:249. 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=4,CE= ,则△ABC的面积为( ) A、8 B、15 C、9 D、1210. 如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点且AE∶EB=4∶1,EF⊥AC于点F,连接FB,则tan∠CFB的值等于( )
A、8 B、15 C、9 D、1210. 如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点且AE∶EB=4∶1,EF⊥AC于点F,连接FB,则tan∠CFB的值等于( ) A、 B、 C、 D、5
A、 B、 C、 D、5二、填空题
-
11. 用配方法解一元二次方程2x2+3x+1=0,变形为(x+h)2=k,则h= , k= .12. 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段 的长为 .
 13. 关于x的方程a(x+m)2=c的解是x1=3,x2=﹣2(a,m,b均为常数,a≠0),则方程a(x+m+2)2=c的解是14. 高淳区去年螃蟹放养面积为20万亩,每亩产量为40kg,为满足市场需要,今年该区扩大了放养面积,并且全部放养了高产的新品种螃蟹.已知今年螃蟹的总产量为1500万kg,且螃蟹放养面积的增长率是亩产量的增长率的2倍,求该区今年螃蟹的亩产量.设亩产量的增长率为x列方程为15. 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=5 ,则BD的长为 .
13. 关于x的方程a(x+m)2=c的解是x1=3,x2=﹣2(a,m,b均为常数,a≠0),则方程a(x+m+2)2=c的解是14. 高淳区去年螃蟹放养面积为20万亩,每亩产量为40kg,为满足市场需要,今年该区扩大了放养面积,并且全部放养了高产的新品种螃蟹.已知今年螃蟹的总产量为1500万kg,且螃蟹放养面积的增长率是亩产量的增长率的2倍,求该区今年螃蟹的亩产量.设亩产量的增长率为x列方程为15. 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=5 ,则BD的长为 . 16. 矩形纸片ABCD,长AD=8cm,宽AB=4cm,折叠纸片,使折痕经过点B,交AD边于点E,点A落在点A'处,展平后得到折痕BE,同时得到线段BA',EA',不再添加其它线段.当图中存在30°角时,AE的长为厘米.
16. 矩形纸片ABCD,长AD=8cm,宽AB=4cm,折叠纸片,使折痕经过点B,交AD边于点E,点A落在点A'处,展平后得到折痕BE,同时得到线段BA',EA',不再添加其它线段.当图中存在30°角时,AE的长为厘米.
三、解答题
-
17.(1)、x2﹣x=﹣2(x﹣1);(2)、(x+1)(2﹣x)=1;(3)、 ×tan60﹣ .18. 如图,在Rt△ABC中,∠C=90°,AD是角平分线,点E在AC上,AB=9,AD=6,AE=4,∠BAC=50°.求∠CDE的度数.
 19. 如图,某旅游景点要在长、宽分别为20米、12米的矩形水池的正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四角连接四条与矩形的边互相平行且宽度相等的道路,已知道路的宽为正方形边长的 ,若道路与观赏亭的面积之和是矩形水池面积的 ,求道路的宽.
19. 如图,某旅游景点要在长、宽分别为20米、12米的矩形水池的正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四角连接四条与矩形的边互相平行且宽度相等的道路,已知道路的宽为正方形边长的 ,若道路与观赏亭的面积之和是矩形水池面积的 ,求道路的宽. 20. 在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践,如图为实践时绘制的截面图.无人机从地面点B垂直起飞到达点A处,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和D , 点B为CD的中点,求2号楼的高度.(结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)
20. 在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践,如图为实践时绘制的截面图.无人机从地面点B垂直起飞到达点A处,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和D , 点B为CD的中点,求2号楼的高度.(结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)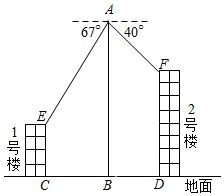 21. 已知关于 的一元二次方程 有两个不相等的实数根(1)、求 的取值范围;(2)、若 为正整数,且该方程的根都是整数,求 的值。22. 如图,四边形 和四边形 均为菱形,且 .点 在线段 上,已知 , ,且 ,连接 , ,求 的长.
21. 已知关于 的一元二次方程 有两个不相等的实数根(1)、求 的取值范围;(2)、若 为正整数,且该方程的根都是整数,求 的值。22. 如图,四边形 和四边形 均为菱形,且 .点 在线段 上,已知 , ,且 ,连接 , ,求 的长. 23. 如图,正方形ABCD的边长为1,对角线AC与BD相交于点O,点P是AB边上的一个动点(点P不与点A、B重合),CP与BD相交于点Q.
23. 如图,正方形ABCD的边长为1,对角线AC与BD相交于点O,点P是AB边上的一个动点(点P不与点A、B重合),CP与BD相交于点Q. (1)、若CP平分∠ACB,求证:AP=2QO.(2)、先按下列要求画出相应图形,然后求解问题.①把线段PC绕点P旋转90°,使点C落在点E处,并连接AE.设线段BP的长度为x,△APE的面积为S.试求S与x的函数关系式;②求出S的最大值,判断此时点P所在的位置.24. 平面直角坐标系xOy中,直线y=﹣ x+3与x、y轴交于A、B两点,与正化例函数y=kx的图像交于点F,CE∥x轴,点C坐标为(0,m)(0<m<3),以BC、BE为邻边作平行四边形BCDE当点D在OF上时,m=2.
(1)、若CP平分∠ACB,求证:AP=2QO.(2)、先按下列要求画出相应图形,然后求解问题.①把线段PC绕点P旋转90°,使点C落在点E处,并连接AE.设线段BP的长度为x,△APE的面积为S.试求S与x的函数关系式;②求出S的最大值,判断此时点P所在的位置.24. 平面直角坐标系xOy中,直线y=﹣ x+3与x、y轴交于A、B两点,与正化例函数y=kx的图像交于点F,CE∥x轴,点C坐标为(0,m)(0<m<3),以BC、BE为邻边作平行四边形BCDE当点D在OF上时,m=2. (1)、求直线OF的函数解析式;(2)、设平行四边形BCDE与△BOF重叠部分面积为S,求S与m的关系式,并直接写出自变量m的取值范围25. 在△ABC中,AB=AC,D、E分别是AB、AC上的点,∠ADE=∠AEB,AF平分∠BAC交DE于G,交BE于F
(1)、求直线OF的函数解析式;(2)、设平行四边形BCDE与△BOF重叠部分面积为S,求S与m的关系式,并直接写出自变量m的取值范围25. 在△ABC中,AB=AC,D、E分别是AB、AC上的点,∠ADE=∠AEB,AF平分∠BAC交DE于G,交BE于F (1)、在图1中找1条和EF相等得线段,并证明;(2)、如图2,延长DE与BC交于点H,若AG=kGF,猜想并验证BC与CH的数量关系(用含k得式子表示)26. 学校围建一个矩形场地,要求矩形场地的一面利用一段长为35m的旧墙,其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,设计划新建墙的总长度为am,利用的旧墙的长度为xm.
(1)、在图1中找1条和EF相等得线段,并证明;(2)、如图2,延长DE与BC交于点H,若AG=kGF,猜想并验证BC与CH的数量关系(用含k得式子表示)26. 学校围建一个矩形场地,要求矩形场地的一面利用一段长为35m的旧墙,其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,设计划新建墙的总长度为am,利用的旧墙的长度为xm. (1)、当a=48时,试确定使矩形场地的面积为200的x值;(2)、已知新建墙的成本与墙的长度满足函数关系w=200a+1000,若计划投入13000元全部用于围墙的建设,求围建后的面积能否达到500m2 .
(1)、当a=48时,试确定使矩形场地的面积为200的x值;(2)、已知新建墙的成本与墙的长度满足函数关系w=200a+1000,若计划投入13000元全部用于围墙的建设,求围建后的面积能否达到500m2 .