广东省佛山市顺德区2021-2022学年九年级上学期10月月考数学试题
试卷更新日期:2021-11-30 类型:月考试卷
一、单选题
-
1. 下列关于四边形的说法,正确的是( )A、四个角都是直角的四边形是正方形 B、对角线互相垂直的四边形是菱形 C、有两边相等的平行四边形是菱形 D、两条对角线相等的菱形是正方形2. 若直角三角形的斜边长为12,则斜边上的中线长为( )A、6 B、8 C、10 D、123. 若菱形的周长为16,高为2,则菱形的面积为( )A、4 B、6 C、8 D、324. 把方程 化成一元二次方程的一般形式,则二次项系数、一次项系数、常数项分别是( )A、2,1,0 B、2,-5,0 C、2,-3,-1 D、2,5,05. 已知关于x的方程mx2﹣2x+1=0有两个不相等的实数根,则m的取值范围是( )A、m<1 B、m>1 C、m<1,且m≠0 D、m>1,且m≠06. 用配方法解方程 ,配方后的方程是( )A、 B、 C、 D、7. 如图,在 中,点 是 上一点, 交 于点 , , ,则 与 的比是( )
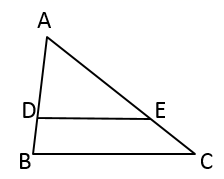 A、 B、 C、 D、8. 如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠E的度数为( )
A、 B、 C、 D、8. 如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠E的度数为( ) A、70° B、80° C、90° D、120°9. 在一个不透明的盒子中装有20个黄、白两种颜色的乒乓球,除颜色外其它都相同,小明进行了多次摸球实验,发现摸到白色乒乓球的频率稳定在0.2左右,由此可知盒子中黄色乒乓球的个数可能是( )A、2个 B、4个 C、18个 D、16个10. 若a,b为方程 的两个实数根,则2 的值为( )A、-41 B、-35 C、39 D、45
A、70° B、80° C、90° D、120°9. 在一个不透明的盒子中装有20个黄、白两种颜色的乒乓球,除颜色外其它都相同,小明进行了多次摸球实验,发现摸到白色乒乓球的频率稳定在0.2左右,由此可知盒子中黄色乒乓球的个数可能是( )A、2个 B、4个 C、18个 D、16个10. 若a,b为方程 的两个实数根,则2 的值为( )A、-41 B、-35 C、39 D、45二、填空题
-
11. 方程 x2-4x=0的实数解是 .12. 已知 , 是一元二次方程 的两根,则 .13. 已知 ,则 的值为 .14. 如图,在矩形ABCD中,AD>AB,AB=2.点E在矩形ABCD的边BC上,连结AE,将矩形ABCD沿AE翻折,翻折后的点B落在边AD上的点F处,得到矩形CDFE.若矩形CDFE与原矩形ABCD相似,则AD的长为 .
 15. 如图,矩形 的对角线 与 相交点 , , , , 分别为 , 的中点,则 的长度为 .
15. 如图,矩形 的对角线 与 相交点 , , , , 分别为 , 的中点,则 的长度为 . 16. 如图所示的电路图中,当随机闭合 , , , 中的两个开关时,能够让灯泡发光的概率为 .
16. 如图所示的电路图中,当随机闭合 , , , 中的两个开关时,能够让灯泡发光的概率为 .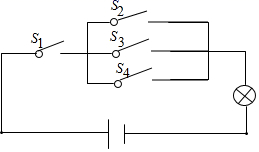 17. 两张宽为 的纸条交叉重叠成四边形 ,如图所示.若 ,则对角线 上的动点 到 三点距离之和的最小值是 .
17. 两张宽为 的纸条交叉重叠成四边形 ,如图所示.若 ,则对角线 上的动点 到 三点距离之和的最小值是 .
三、解答题
-
18. 如图, ,直线 , 交于点 ,且分别与直线 , , 交于点 , , 和点 , , ,已知 , , , ,求 的长度.
 19. 解方程:2x2=3x-120. 学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校,某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为了三类; :好, :中, :差,请根据图中信息,解答下列问题:
19. 解方程:2x2=3x-120. 学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校,某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为了三类; :好, :中, :差,请根据图中信息,解答下列问题: (1)、在扇形统计图中, , , 类的圆心角为 .(2)、张老师在班上随机抽取了4名学生,其中 类1人, 类2人, 类1人,若再从这4人中随机抽取2人,请求出全是 类学生的概率.21. 如图所示,利用一面墙,用40m的篱笆围成一个150m2的矩形ABCD场地.
(1)、在扇形统计图中, , , 类的圆心角为 .(2)、张老师在班上随机抽取了4名学生,其中 类1人, 类2人, 类1人,若再从这4人中随机抽取2人,请求出全是 类学生的概率.21. 如图所示,利用一面墙,用40m的篱笆围成一个150m2的矩形ABCD场地. (1)、若墙长不限,求矩形ABCD的边AB,BC分别为多少?(2)、若墙长13m,利用(1)题的计算结果,说明具体围法.22. 如图,菱形 的对角线 , 相交于点 ,点 是 的中点,连接 .已知 , .
(1)、若墙长不限,求矩形ABCD的边AB,BC分别为多少?(2)、若墙长13m,利用(1)题的计算结果,说明具体围法.22. 如图,菱形 的对角线 , 相交于点 ,点 是 的中点,连接 .已知 , . (1)、求 的长度;(2)、求点 到 的距离.23. 某药店新进一批桶装消毒液,每桶进价30元,原计划以每桶50元的价格销售,为更好地助力疫情防控,现决定降价销售,已知这种消毒液销售量 (桶)与每桶降价 (元) 之间满足一次函数关系,其图象如所示.
(1)、求 的长度;(2)、求点 到 的距离.23. 某药店新进一批桶装消毒液,每桶进价30元,原计划以每桶50元的价格销售,为更好地助力疫情防控,现决定降价销售,已知这种消毒液销售量 (桶)与每桶降价 (元) 之间满足一次函数关系,其图象如所示. (1)、求 与 之间的函数表达式;(2)、在这次助力疫情防控活动中,该药店仅获利1610元.请问这种消毒液每桶实际售价多少元?
(1)、求 与 之间的函数表达式;(2)、在这次助力疫情防控活动中,该药店仅获利1610元.请问这种消毒液每桶实际售价多少元?
