安徽省合肥五十中西校2021-2022学年九年级上学期第一次月考数学试题
试卷更新日期:2021-11-30 类型:月考试卷
一、单选题
-
1. 下列函数中是二次函数的是( )A、y=x+1 B、 C、y=ax2+bx+c D、y=x22. 二次函数 图像的顶点坐标是( )A、 B、 C、 D、3. 将二次函数y=﹣ x2的图象向左平移2个单位,则平移后的二次函数的表达式为( )A、y= x2﹣2 B、y= x2+2 C、y= (x+2)2 D、y= (x﹣2)24. 如表给出了二次函数y=x2+2x﹣5中x,y的一些对应值,则可以估计一元二次方程x2+2x﹣5=0的一个近似解(精确到0.1)为( )
x
…
1.2
1.3
1.4
1.5
1.6
…
y
…
﹣1.16
﹣0.71
﹣0.24
0.25
0.76
…
A、1.3 B、1.4 C、1.5 D、1.65. 据省统计局公布的数据,合肥市2021年第一季度GDP总值约为2.4千亿元人民币,若我市第三季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )A、 B、 C、 D、6. 已知二次函数 ,下列说法中正确的是( )A、该函数图象的开口向下 B、该函数图象的最大值是﹣7 C、当x<0时,y随x的增大而增大 D、该函数图象与x轴有两个不同的交点,且分布在坐标原点的两侧7. 若函数y=(a﹣1)x2﹣4x+2a的图象与x轴有且只有一个交点,则a的值为( ).A、-1 B、2 C、-1或2 D、-1或2或18. 在同一直角坐标系中,函数 和函数 ( 是常数,且 ) 的图像可能是( )A、 B、
B、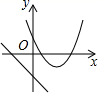 C、
C、 D、
D、 9. 已知两点A(x1 , y1)、B(x2 , y2)均在抛物线y=﹣ax2﹣4ax+c上(a≠0),若|x1+2|≤|x2+2|,并且当x取﹣1时对应的函数值大于x取0时对应的函数值,则y1 , y2的大小关系是( )A、y1≥y2 B、y1≤y2 C、y1>y2 D、y1<y210. 如图是二次函数 的图象的一部分,给出下列命题:①b=a;②a﹣3b+c=0;③a﹣2b+c>0;④m(am+b)≥a﹣b(m为任意实数),其中正确的命题有( )
9. 已知两点A(x1 , y1)、B(x2 , y2)均在抛物线y=﹣ax2﹣4ax+c上(a≠0),若|x1+2|≤|x2+2|,并且当x取﹣1时对应的函数值大于x取0时对应的函数值,则y1 , y2的大小关系是( )A、y1≥y2 B、y1≤y2 C、y1>y2 D、y1<y210. 如图是二次函数 的图象的一部分,给出下列命题:①b=a;②a﹣3b+c=0;③a﹣2b+c>0;④m(am+b)≥a﹣b(m为任意实数),其中正确的命题有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
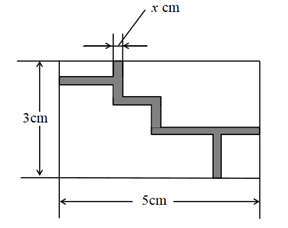
11. 抛物线 与 轴交于 , 两点,则 , 两点之间的距离是 .12. 如图,是一个迷宫游戏盘的局部平面简化示意图,该矩形的长、宽分别为5cm,3cm,其中阴影部分为迷宫中的挡板,设挡板的宽度为xcm,小球滚动的区域(空白区域)面积为ycm2 . 则y关于x的函数关系式为:(化简为一般式).
 13. 某种型号的小型无人机着陆后滑行的距离S(单位:米)关于滑行的时间t(单位:秒)的函数解析式是S=10t﹣0.25t2 , 无人机着陆后滑行秒才能停下来.14. 平面直角坐标系中,已知点A(1,2),B(2,3),C(2,1),抛物线y=ax2+bx+1恰好经过A,B,C中的两点.(1)、请判断并写出该抛物线经过A,B,C中的两点;(2)、平移抛物线y=ax2+bx+1,使其顶点在直线y=x+1上,设平移后抛物线顶点的横坐标为m.则平移后的抛物线与y轴交点纵坐标的最大值为 .
13. 某种型号的小型无人机着陆后滑行的距离S(单位:米)关于滑行的时间t(单位:秒)的函数解析式是S=10t﹣0.25t2 , 无人机着陆后滑行秒才能停下来.14. 平面直角坐标系中,已知点A(1,2),B(2,3),C(2,1),抛物线y=ax2+bx+1恰好经过A,B,C中的两点.(1)、请判断并写出该抛物线经过A,B,C中的两点;(2)、平移抛物线y=ax2+bx+1,使其顶点在直线y=x+1上,设平移后抛物线顶点的横坐标为m.则平移后的抛物线与y轴交点纵坐标的最大值为 .三、解答题
-
15. 求证:抛物线y=x2+mx+m﹣2与x轴必有两个不同的交点.16. 已知二次函数 .(1)、请将下表填写完整,并在网格中画出该二次函数图象;
x
…
﹣1
0
1
2
3
…
y
…
3
0
…
 (2)、若A(﹣ ,y1),B(2,y2),C( ,y3)是该函数图象上的三点,请比较y1 , y2 , y3之间的大小关系(直接写出结果)17. 二次函数 的图象如图所示,根据图象解答下列问题.
(2)、若A(﹣ ,y1),B(2,y2),C( ,y3)是该函数图象上的三点,请比较y1 , y2 , y3之间的大小关系(直接写出结果)17. 二次函数 的图象如图所示,根据图象解答下列问题. (1)、写出方程 的两个根:;(2)、写出不等式 的解集:;(3)、写出 随 的增大而减小的自变量 的取值范围;(4)、若方程 有两个不相等的实数根,直接写出 的取值范围: .18. 如图,一辆宽为2米的货车要通过跨度为8米,拱高为4米的单行抛物线隧道(从正中通过),抛物线满足表达式y=﹣ x2+4.保证安全,车顶离隧道的顶部至少要有0.5米的距离,求货车的限高应是多少.
(1)、写出方程 的两个根:;(2)、写出不等式 的解集:;(3)、写出 随 的增大而减小的自变量 的取值范围;(4)、若方程 有两个不相等的实数根,直接写出 的取值范围: .18. 如图,一辆宽为2米的货车要通过跨度为8米,拱高为4米的单行抛物线隧道(从正中通过),抛物线满足表达式y=﹣ x2+4.保证安全,车顶离隧道的顶部至少要有0.5米的距离,求货车的限高应是多少. 19. 阅读材料:设二次函数y1 , y2的图象的顶点坐标分别为(h,k),(m,n),若h=2m,k=2n,且开口方向相同,则称y1是y2的“同倍二次函数”.(1)、请写出二次函数y=x2﹣2x+2的一个“同倍二次函数”;(2)、已知关于x的二次函数y1=(x﹣ )2﹣ 和二次函数y2=2x2﹣ax+1,若函数y1恰是y2的“同倍二次函数”,求a的值.20. 如图,某小区有一块靠墙(墙的长度不限)的矩形ABCD,为美化环境,用总长为90m的篱笆围成四块矩形,其中S1=S2=S3= S4(靠墙一侧不用篱笆,其余部分均使用,篱笆的厚度不计).
19. 阅读材料:设二次函数y1 , y2的图象的顶点坐标分别为(h,k),(m,n),若h=2m,k=2n,且开口方向相同,则称y1是y2的“同倍二次函数”.(1)、请写出二次函数y=x2﹣2x+2的一个“同倍二次函数”;(2)、已知关于x的二次函数y1=(x﹣ )2﹣ 和二次函数y2=2x2﹣ax+1,若函数y1恰是y2的“同倍二次函数”,求a的值.20. 如图,某小区有一块靠墙(墙的长度不限)的矩形ABCD,为美化环境,用总长为90m的篱笆围成四块矩形,其中S1=S2=S3= S4(靠墙一侧不用篱笆,其余部分均使用,篱笆的厚度不计). (1)、若AE=x,用含有x的式子表示BE的长;(2)、求矩形ABCD的面积y关于x的解析式,并直接写出当面积取得最大值时,AE的长.21. 如图、在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣2,4),过点A作AB⊥y轴,垂足为B、连接OA,若抛物线 经过点 A.
(1)、若AE=x,用含有x的式子表示BE的长;(2)、求矩形ABCD的面积y关于x的解析式,并直接写出当面积取得最大值时,AE的长.21. 如图、在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣2,4),过点A作AB⊥y轴,垂足为B、连接OA,若抛物线 经过点 A. (1)、求c的值;(2)、将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在 OAB的内部(不包括 OAB的边界),直接写出m的取值范围;(3)、若点P为抛物线上一动点,求使 时点 P的坐标.22. 如图,抛物线y=﹣x2+ x+2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过B,C两点,点D为抛物线上一个动点(不与B,C重合).
(1)、求c的值;(2)、将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在 OAB的内部(不包括 OAB的边界),直接写出m的取值范围;(3)、若点P为抛物线上一动点,求使 时点 P的坐标.22. 如图,抛物线y=﹣x2+ x+2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过B,C两点,点D为抛物线上一个动点(不与B,C重合). (1)、求直线l的表达式;(2)、如图,当点D在直线l上方的抛物线上时,过D点作DE x轴交直线l于点E,设点D的横坐标为m.
(1)、求直线l的表达式;(2)、如图,当点D在直线l上方的抛物线上时,过D点作DE x轴交直线l于点E,设点D的横坐标为m.①当点D运动到使得点E与点C重合时,求点D的坐标;
②求线段DE的长(用含m的代数式表示),并求出线段DE的最大值.
23. 某产品每件成本为20元,经过市场调研发现,这种产品在未来20天内的日销售量 (单位 件)关于时间 (单位:天)的函数关系式为: ,这20天中,该产品每天的价格 (单位:元)与时间t(单位;天)的函效关系式为; ( 为整数),根据以上提供的条件解决下列问题:(1)、设日销售利润为 (元),直接写出 关于 的函数关系式;(2)、这20天中哪一天的日销售利润最大,最大的销售利润是多少?(3)、在实际销售的20天中,每销售一件商品就捐赠 元 给希望工程,通过销售记录发现.这20天中,每天扣除捐赠后的日销利润随时间 的增大而增大,求 的取值范围.