2021-2022学年北师版数学九年级下册《第二章 二次函数》单元检测A卷
试卷更新日期:2021-11-29 类型:单元试卷
一、单选题
-
1. 二次函数 的图象的对称轴是( )A、 B、 C、 D、2. 在平面直角坐标系中,将二次函数 的图象向左平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数表达式为( )A、 B、 C、 D、3. 如图,抛物线 与 轴只有一个公共点A(1,0),与 轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线 ,则图中两个阴影部分的面积和为( )
 A、1 B、2 C、3 D、44. 已知二次函数 ,当 时,y随x增大而增大,则实数a的取值范围是( )A、 B、 C、 D、5. 一次函数 的图象如图所示,则二次函数 的图象可能是( )
A、1 B、2 C、3 D、44. 已知二次函数 ,当 时,y随x增大而增大,则实数a的取值范围是( )A、 B、 C、 D、5. 一次函数 的图象如图所示,则二次函数 的图象可能是( )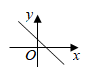 A、
A、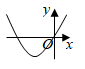 B、
B、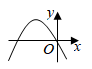 C、
C、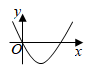 D、
D、 6. 已知二次函数y=ax2+bx+c的自变量x与函数y的部分对应值见表格,则下列结论:①c=2;②b2﹣4ac>0;③方程ax2+bx=0的两根为x1=﹣2,x2=0;④7a+c<0.其中正确的有( )
6. 已知二次函数y=ax2+bx+c的自变量x与函数y的部分对应值见表格,则下列结论:①c=2;②b2﹣4ac>0;③方程ax2+bx=0的两根为x1=﹣2,x2=0;④7a+c<0.其中正确的有( )x
…
﹣3
﹣2
﹣1
1
2
…
y
…
1.875
3
m
1.875
0
…
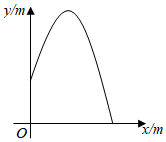
A、①④ B、②③ C、③④ D、②④7. 如图, 为矩形 的对角线,已知 , .点P沿折线 以每秒1个单位长度的速度运动(运动到D点停止),过点P作 于点E,则 的面积y与点P运动的路程x间的函数图象大致是( ) A、
A、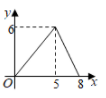 B、
B、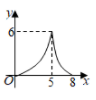 C、
C、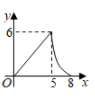 D、
D、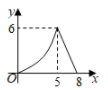 8. 已知抛物线 与 轴有两个交点 , ,抛物线 与 轴的一个交点是 ,则 的值是( )A、5 B、1 C、5或1 D、-5或-19. 在平面直角坐标系中,抛物线 与 轴交于点 ,则该抛物线关于点 成中心对称的抛物线的表达式为( )A、 B、 C、 D、10. 二次函数 的图象如图所示,有下列结论:① ,② ,③ ,④ ,正确的有( )
8. 已知抛物线 与 轴有两个交点 , ,抛物线 与 轴的一个交点是 ,则 的值是( )A、5 B、1 C、5或1 D、-5或-19. 在平面直角坐标系中,抛物线 与 轴交于点 ,则该抛物线关于点 成中心对称的抛物线的表达式为( )A、 B、 C、 D、10. 二次函数 的图象如图所示,有下列结论:① ,② ,③ ,④ ,正确的有( ) A、1个 B、2个 C、3个 D、4个11. 抛物线 (a,b,c为常数)开口向下且过点 , ( ),下列结论:① ;② ;③ ;④若方程 有两个不相等的实数根,则 .其中正确结论的个数是( )A、4 B、3 C、2 D、112. 定义: ,若函数 ,则该函数的最大值为( )A、0 B、2 C、3 D、4
A、1个 B、2个 C、3个 D、4个11. 抛物线 (a,b,c为常数)开口向下且过点 , ( ),下列结论:① ;② ;③ ;④若方程 有两个不相等的实数根,则 .其中正确结论的个数是( )A、4 B、3 C、2 D、112. 定义: ,若函数 ,则该函数的最大值为( )A、0 B、2 C、3 D、4二、填空题
-
13. 二次函数 的图象开口方向是(填“向上”或“向下”).14. 从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度 (单位: )与它距离喷头的水平距离 (单位: )之间满足函数关系式 ,喷出水珠的最大高度是 .
 15. 抛物线y=ax2+bx+c(a,b,c为常数,a>0)经过(0,0),(4,0)两点.则下列四个结论正确的有 (填写序号).
15. 抛物线y=ax2+bx+c(a,b,c为常数,a>0)经过(0,0),(4,0)两点.则下列四个结论正确的有 (填写序号).①4a+b=0;
②5a+3b+2c>0;
③若该抛物线y=ax2+bx+c与直线y=﹣3有交点,则a的取值范围是a ;
④对于a的每一个确定值,如果一元二次方程ax2+bx+c﹣t=0(t为常数,t≤0)的根为整数,则t的值只有3个.
16. 在平面直角坐标系 中,若抛物线 与x轴只有一个交点,则 .17. 以初速度v(单位:m/s)从地面竖直向上抛出小球,从抛出到落地的过程中,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=vt﹣4.9t2.现将某弹性小球从地面竖直向上抛出,初速度为v1 , 经过时间t1落回地面,运动过程中小球的最大高度为h1(如图1);小球落地后,竖直向上弹起,初速度为v2 , 经过时间t2落回地面,运动过程中小球的最大高度为h2(如图2).若h1=2h2 , 则t1:t2=. 18. 某快餐店销售A、B两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是元.
18. 某快餐店销售A、B两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是元.三、解答题
-
19. 农技人员对培育的某一品种桃树进行研究,发现桃子成熟后一棵树上每个桃子质量大致相同.以每棵树上桃子的数量x(个)为横坐标、桃子的平均质量y(克/个)为纵坐标,在平面直角坐标系中描出对应的点,发现这些点大致分布在直线AB附近(如图所示).
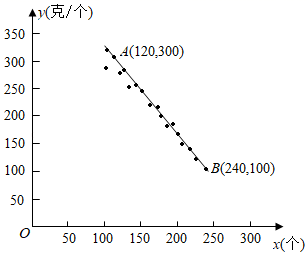 (1)、求直线AB的函数关系式;(2)、市场调研发现:这个品种每个桃子的平均价格w(元)与平均质量y(克/个)满足函数表达式w= y+2.在(1)的情形下,求一棵树上桃子数量为多少时,该树上的桃子销售额最大?20. 如图,点 在函数 的图象上.已知 的横坐标分别为-2、4,直线 与 轴交于点 ,连接 .
(1)、求直线AB的函数关系式;(2)、市场调研发现:这个品种每个桃子的平均价格w(元)与平均质量y(克/个)满足函数表达式w= y+2.在(1)的情形下,求一棵树上桃子数量为多少时,该树上的桃子销售额最大?20. 如图,点 在函数 的图象上.已知 的横坐标分别为-2、4,直线 与 轴交于点 ,连接 .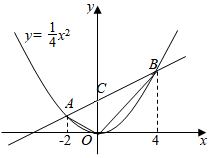 (1)、求直线 的函数表达式;(2)、求 的面积;(3)、若函数 的图象上存在点 ,使得 的面积等于 的面积的一半,则这样的点 共有个.21. 如图,已知抛物线 经过 , 两点,交 轴于点 .
(1)、求直线 的函数表达式;(2)、求 的面积;(3)、若函数 的图象上存在点 ,使得 的面积等于 的面积的一半,则这样的点 共有个.21. 如图,已知抛物线 经过 , 两点,交 轴于点 . (1)、求抛物线的解析式;(2)、连接 ,求直线 的解析式;(3)、请在抛物线的对称轴上找一点 ,使 的值最小,求点 的坐标,并求出此时 的最小值;(4)、点 为 轴上一动点,在抛物线上是否存在一点 ,使得以 、 、 、 四点为顶点的四边形是平行四边形?若存在,求出点 的坐标;若不存在,请说明理由.22. 某公司电商平台,在2021年五一长假期间,举行了商品打折促销活动,经市场调查发现,某种商品的周销售量y(件)是关于售价x(元/件)的一次函数,下表仅列出了该商品的售价x,周销售量y,周销售利润W(元)的三组对应值数据.
(1)、求抛物线的解析式;(2)、连接 ,求直线 的解析式;(3)、请在抛物线的对称轴上找一点 ,使 的值最小,求点 的坐标,并求出此时 的最小值;(4)、点 为 轴上一动点,在抛物线上是否存在一点 ,使得以 、 、 、 四点为顶点的四边形是平行四边形?若存在,求出点 的坐标;若不存在,请说明理由.22. 某公司电商平台,在2021年五一长假期间,举行了商品打折促销活动,经市场调查发现,某种商品的周销售量y(件)是关于售价x(元/件)的一次函数,下表仅列出了该商品的售价x,周销售量y,周销售利润W(元)的三组对应值数据.x
40
70
90
y
180
90
30
W
3600
4500
2100
(1)、求y关于x的函数解析式(不要求写出自变量的取值范围);(2)、若该商品进价a(元/件),售价x为多少时,周销售利润W最大?并求出此时的最大利润;(3)、因疫情期间,该商品进价提高了m(元/件)( ),公司为回馈消费者,规定该商品售价x不得超过55(元/件),且该商品在今后的销售中,周销售量与售价仍满足(1)中的函数关系,若周销售最大利润是4050元,求m的值.23. 如图,抛物线 与 轴交于A、B(3,0)两点,与 轴交于点C(0,-3),抛物线的顶点为D.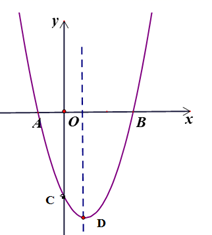 (1)、求抛物线的解析式;(2)、点P在抛物线的对称轴上,点Q在 轴上,若以点P、Q、B、C为顶点,BC为边的四边形为平行四边形,请直接写出点P、Q的坐标;(3)、已知点M是 轴上的动点,过点M作 的垂线交抛物线于点G,是否存在这样的点M,使得以点A、M、G为顶点的三角形与△BCD相似,若存在,请求出点M的坐标;若不存在,请说明理由.24. 甲秀楼是贵阳市一张靓丽的名片.如图①,甲秀楼的桥拱截面 可视为抛物线的一部分,在某一时刻,桥拱内的水面宽 ,桥拱顶点 到水面的距离是 .
(1)、求抛物线的解析式;(2)、点P在抛物线的对称轴上,点Q在 轴上,若以点P、Q、B、C为顶点,BC为边的四边形为平行四边形,请直接写出点P、Q的坐标;(3)、已知点M是 轴上的动点,过点M作 的垂线交抛物线于点G,是否存在这样的点M,使得以点A、M、G为顶点的三角形与△BCD相似,若存在,请求出点M的坐标;若不存在,请说明理由.24. 甲秀楼是贵阳市一张靓丽的名片.如图①,甲秀楼的桥拱截面 可视为抛物线的一部分,在某一时刻,桥拱内的水面宽 ,桥拱顶点 到水面的距离是 .
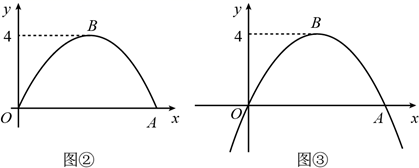 (1)、按如图②所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式;(2)、一只宽为 的打捞船径直向桥驶来,当船驶到桥拱下方且距 点 时,桥下水位刚好在 处.有一名身高 的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱,请说明理由(假设船底与水面齐平);(3)、如图③,桥拱所在的函数图象是抛物线 ,该抛物线在 轴下方部分与桥拱 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 个单位长度,平移后的函数图象在 时, 的值随 值的增大而减小,结合函数图象,求 的取值范围.
(1)、按如图②所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式;(2)、一只宽为 的打捞船径直向桥驶来,当船驶到桥拱下方且距 点 时,桥下水位刚好在 处.有一名身高 的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱,请说明理由(假设船底与水面齐平);(3)、如图③,桥拱所在的函数图象是抛物线 ,该抛物线在 轴下方部分与桥拱 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 个单位长度,平移后的函数图象在 时, 的值随 值的增大而减小,结合函数图象,求 的取值范围.