2021-2022学年北师版数学九年级下册《第一章 直角三角形的边角关系》单元检测B卷
试卷更新日期:2021-11-29 类型:单元试卷
一、单选题
-
1. sin45°的值是( )A、 B、 C、 D、12. 如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是( )
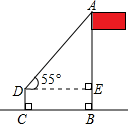 A、tan55°= B、tan55°= C、sin55°= D、cos55°=3. 如图,矩形AOBC的顶点A、B在坐标轴上,点C的坐标是(﹣10,8),点D在AC上,将 BCD沿BD翻折,点C恰好落在OA边上点E处,则tan∠DBE等于( )
A、tan55°= B、tan55°= C、sin55°= D、cos55°=3. 如图,矩形AOBC的顶点A、B在坐标轴上,点C的坐标是(﹣10,8),点D在AC上,将 BCD沿BD翻折,点C恰好落在OA边上点E处,则tan∠DBE等于( )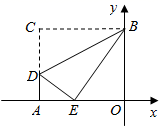 A、 B、 C、 D、4. 在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )A、 B、 C、 D、5. 如图是一架人字梯,已知 米,AC与地面BC的夹角为 ,则两梯脚之间的距离BC为( )
A、 B、 C、 D、4. 在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )A、 B、 C、 D、5. 如图是一架人字梯,已知 米,AC与地面BC的夹角为 ,则两梯脚之间的距离BC为( )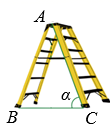 A、 米 B、 米 C、 米 D、 米6. 如图,在 中, , , ,将 绕点A逆时针旋转得到 ,使点 落在AB边上,连结 ,则 的值为( )
A、 米 B、 米 C、 米 D、 米6. 如图,在 中, , , ,将 绕点A逆时针旋转得到 ,使点 落在AB边上,连结 ,则 的值为( ) A、 B、 C、 D、7. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 .据此,可求得学校与工厂之间的距离 等于( )
A、 B、 C、 D、7. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 .据此,可求得学校与工厂之间的距离 等于( )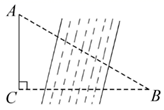 A、 B、 C、 D、8. 如图, 底边 上的高为 , 底边 上的高为 ,则有( )
A、 B、 C、 D、8. 如图, 底边 上的高为 , 底边 上的高为 ,则有( )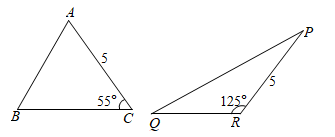 A、 B、 C、 D、以上都有可能9. 如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O, 于E点,交BD于M点,反比例函数 的图象经过线段DC的中点N,若 ,则ME的长为( )
A、 B、 C、 D、以上都有可能9. 如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O, 于E点,交BD于M点,反比例函数 的图象经过线段DC的中点N,若 ,则ME的长为( )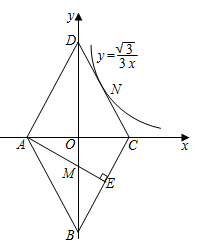 A、 B、 C、 D、10. 如图,将长、宽分别为12cm,3cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )
A、 B、 C、 D、10. 如图,将长、宽分别为12cm,3cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )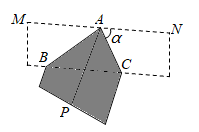 A、(36 )cm2 B、(36 )cm2 C、24cm2 D、36cm211. 如图是某商场营业大厅自动扶梯的示意图.自动扶梯 的倾斜角为 ,大厅两层之间的距离 为6米,则自动扶梯 的长约为( )( ).
A、(36 )cm2 B、(36 )cm2 C、24cm2 D、36cm211. 如图是某商场营业大厅自动扶梯的示意图.自动扶梯 的倾斜角为 ,大厅两层之间的距离 为6米,则自动扶梯 的长约为( )( ).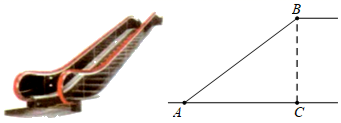 A、7.5米 B、8米 C、9米 D、10米12. 如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为 ,坡顶D到BC的垂直距离 米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶A点的仰角为50°,则建筑物AB的高度约为(参考数据: ; ; )
A、7.5米 B、8米 C、9米 D、10米12. 如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为 ,坡顶D到BC的垂直距离 米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶A点的仰角为50°,则建筑物AB的高度约为(参考数据: ; ; )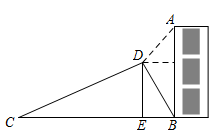 A、69.2米 B、73.1米 C、80.0米 D、85.7米
A、69.2米 B、73.1米 C、80.0米 D、85.7米二、填空题
-
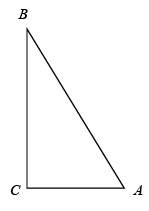
13. 如图,在 中, ,D是 上一点(点D与点A不重合).若在 的直角边上存在4个不同的点分别和点A、D成为直角三角形的三个顶点,则 长的取值范围是.
 14. 如图,Rt△ABC中,∠BAC=90°,tan∠ABC= ,将△ABC绕A点顺时针方向旋转角α(0°<α<90°)得到△AB′C′,连接BB′,CC′,则△CAC′与△BAB′的面积之比等于 .
14. 如图,Rt△ABC中,∠BAC=90°,tan∠ABC= ,将△ABC绕A点顺时针方向旋转角α(0°<α<90°)得到△AB′C′,连接BB′,CC′,则△CAC′与△BAB′的面积之比等于 .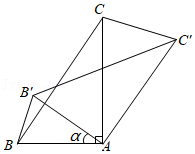 15. 将一副三角板如图放置在平面直角坐标系中,顶点A与原点O重合,AB在x轴正半轴上,且 ,点E在AD上, ,将这副三角板整体向右平移个单位,C,E两点同时落在反比例函数 的图象上.
15. 将一副三角板如图放置在平面直角坐标系中,顶点A与原点O重合,AB在x轴正半轴上,且 ,点E在AD上, ,将这副三角板整体向右平移个单位,C,E两点同时落在反比例函数 的图象上.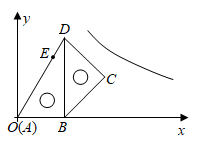 16. 如图,在矩形 中, ,垂足为点 .若 , ,则 的长为.
16. 如图,在矩形 中, ,垂足为点 .若 , ,则 的长为.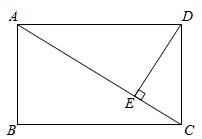 17. 一条上山直道的坡度为1:7,沿这条直道上山,则前进100米所上升的高度为米.18. 如图,已知正方形ABCD边长为1,E为AB边上一点,以点D为中心,将 按逆时针方向旋转得 ,连接EF,分別交BD,CD于点M,N.若 ,则 .
17. 一条上山直道的坡度为1:7,沿这条直道上山,则前进100米所上升的高度为米.18. 如图,已知正方形ABCD边长为1,E为AB边上一点,以点D为中心,将 按逆时针方向旋转得 ,连接EF,分別交BD,CD于点M,N.若 ,则 .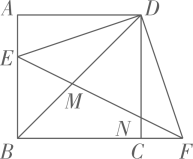
三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 如图,莽山五指峰景区新建了一座垂直观光电梯.某测绘兴趣小组为测算电梯AC的高度,测得斜坡AB=105米,坡度i=1:2,在B处测得电梯顶端C的仰角α=45°,求观光电梯AC的高度.
(参考数据: ≈1.41, ≈1.73, ≈2.24.结果精确到0.1米)
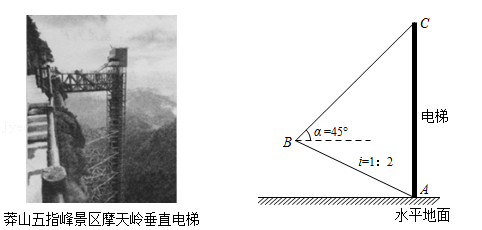 21. 如图, 两点被池塘隔开,在 外选一点C , 连接 .测得 , , .根据测得的数据,求 的长(结果取整数).
21. 如图, 两点被池塘隔开,在 外选一点C , 连接 .测得 , , .根据测得的数据,求 的长(结果取整数).参考数据: , , .
 22. 如图①、图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄 与地面 平行,踏板 长为 , 与地面 的夹角 ,支架 长为 , ,求跑步机手柄 所在直线与地面 之间的距离.(结果精确到 .参考数据: , , , )
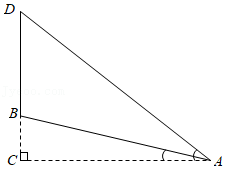
22. 如图①、图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄 与地面 平行,踏板 长为 , 与地面 的夹角 ,支架 长为 , ,求跑步机手柄 所在直线与地面 之间的距离.(结果精确到 .参考数据: , , , ) 23. “2021湖南红色文化旅游节﹣﹣重走青年毛泽东游学社会调查之路”启动仪式于4月29日在安化县梅城镇举行,该镇南面山坡上有一座宝塔,一群爱好数学的学生在研学之余对该宝塔的高度进行了测量.如图所示,在山坡上的A点测得塔底B的仰角∠BAC=13°,塔顶D的仰角∠DAC=38°,斜坡AB=50米,求宝塔BD的高(精确到1米).
23. “2021湖南红色文化旅游节﹣﹣重走青年毛泽东游学社会调查之路”启动仪式于4月29日在安化县梅城镇举行,该镇南面山坡上有一座宝塔,一群爱好数学的学生在研学之余对该宝塔的高度进行了测量.如图所示,在山坡上的A点测得塔底B的仰角∠BAC=13°,塔顶D的仰角∠DAC=38°,斜坡AB=50米,求宝塔BD的高(精确到1米).(参考数据:sin13°≈0.22,cos13°≈0.97,tan13°≈0.23,sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
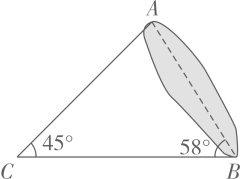
 24. 如图,小明同学在民族广场A处放风筝,风筝位于B处,风筝线AB长为 ,从A处看风筝的仰角为 ,小明的父母从C处看风筝的仰角为 .
24. 如图,小明同学在民族广场A处放风筝,风筝位于B处,风筝线AB长为 ,从A处看风筝的仰角为 ,小明的父母从C处看风筝的仰角为 .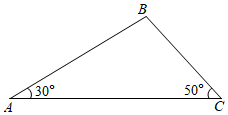 (1)、风筝离地面多少m?(2)、AC相距多少m?(结果保留小数点后一位,参考数据: , , , , , )25. 某种落地灯如图1所示, 为立杆,其高为 ; 为支杆,它可绕点 旋转,其中 长为 ; 为悬杆,滑动悬杆可调节 的长度.支杆 与悬杆 之间的夹角 为 .
(1)、风筝离地面多少m?(2)、AC相距多少m?(结果保留小数点后一位,参考数据: , , , , , )25. 某种落地灯如图1所示, 为立杆,其高为 ; 为支杆,它可绕点 旋转,其中 长为 ; 为悬杆,滑动悬杆可调节 的长度.支杆 与悬杆 之间的夹角 为 .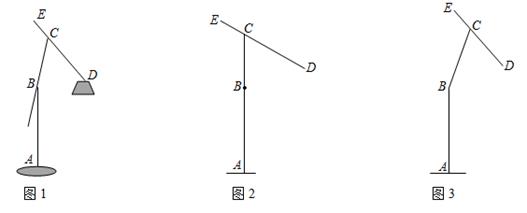 (1)、如图2,当支杆 与地面垂直,且 的长为 时,求灯泡悬挂点 距离地面的高度;(2)、在图2所示的状态下,将支杆 绕点 顺时针旋转 ,同时调节 的长(如图3),此时测得灯泡悬挂点 到地面的距离为 ,求 的长.(结果精确到 ,参考数据: , , , , , )
(1)、如图2,当支杆 与地面垂直,且 的长为 时,求灯泡悬挂点 距离地面的高度;(2)、在图2所示的状态下,将支杆 绕点 顺时针旋转 ,同时调节 的长(如图3),此时测得灯泡悬挂点 到地面的距离为 ,求 的长.(结果精确到 ,参考数据: , , , , , )