2021-2022学年北师版数学九年级下册《第一章 直角三角形的边角关系》单元检测A卷
试卷更新日期:2021-11-29 类型:单元试卷
一、单选题
-
1. 计算 的值为( )A、 B、0 C、 D、2. 如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )
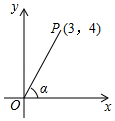 A、 B、 C、 D、3. 如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )
A、 B、 C、 D、3. 如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( ) A、 B、2 C、 D、4. 如图,点A、B、C在边长为1的正方形网格格点上,下列结论错误的是( )
A、 B、2 C、 D、4. 如图,点A、B、C在边长为1的正方形网格格点上,下列结论错误的是( ) A、sinB B、sinC C、tanB D、sin2B+sin2C=15. 如图, 中, , 、 相交于点D, , , ,则 的面积是( )
A、sinB B、sinC C、tanB D、sin2B+sin2C=15. 如图, 中, , 、 相交于点D, , , ,则 的面积是( )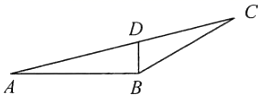 A、 B、 C、 D、6. 规定: 给出以下四个结论:(1) ;(2) ;(3) ;(4) 其中正确的结论的个数为( )A、1个 B、2个 C、3个 D、4个7. 如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转 ,使点B落在点 的位置,连接B ,过点D作DE⊥ ,交 的延长线于点E,则 的长为( )
A、 B、 C、 D、6. 规定: 给出以下四个结论:(1) ;(2) ;(3) ;(4) 其中正确的结论的个数为( )A、1个 B、2个 C、3个 D、4个7. 如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转 ,使点B落在点 的位置,连接B ,过点D作DE⊥ ,交 的延长线于点E,则 的长为( )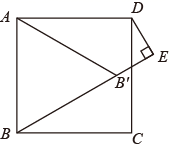 A、 B、 C、 D、8. 如图,菱形 的对角线 与 相交于点 ,点 在 上,连接 , , , , ,则 ( )
A、 B、 C、 D、8. 如图,菱形 的对角线 与 相交于点 ,点 在 上,连接 , , , , ,则 ( )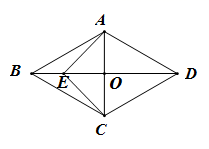 A、4 B、3 C、 D、29. 如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为 时,梯子顶端靠在墙面上的点 处,底端落在水平地面的点 处,现将梯子底端向墙面靠近,使梯子与地面所成角为 ,已知 ,则梯子顶端上升了( )
A、4 B、3 C、 D、29. 如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为 时,梯子顶端靠在墙面上的点 处,底端落在水平地面的点 处,现将梯子底端向墙面靠近,使梯子与地面所成角为 ,已知 ,则梯子顶端上升了( )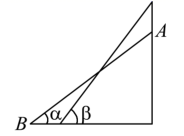 A、1米 B、1.5米 C、2米 D、2.5米10. 如图,小明利用一个锐角是 的三角板测量操场旗杆的高度,已知他与旗杆之间的水平距离 为 , 为 (即小明的眼睛与地面的距离),那么旗杆的高度是( )
A、1米 B、1.5米 C、2米 D、2.5米10. 如图,小明利用一个锐角是 的三角板测量操场旗杆的高度,已知他与旗杆之间的水平距离 为 , 为 (即小明的眼睛与地面的距离),那么旗杆的高度是( )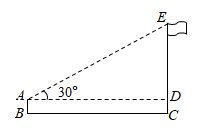 A、 B、 C、 D、11. 如图,拦水坝的横断面为梯形ABCD.其中 , , ,斜坡AB长8m.则斜坡CD的长为( )
A、 B、 C、 D、11. 如图,拦水坝的横断面为梯形ABCD.其中 , , ,斜坡AB长8m.则斜坡CD的长为( )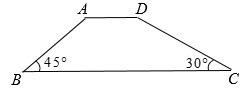 A、 B、 C、 D、12. 如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据: ≈1.732)( )
A、 B、 C、 D、12. 如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据: ≈1.732)( ) A、136.6米 B、86.7米 C、186.7米 D、86.6米
A、136.6米 B、86.7米 C、186.7米 D、86.6米二、填空题
-
13. 计算: .14. 如图,在矩形ABCD中,BD是对角线,AE⊥BD,垂足为E,连接CE,若 ,则tan∠DEC的值是.
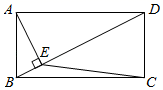 15. 如图,直立于地面上的电线杆 ,在阳光下落在水平地面和坡面上的影子分别是 、 ,测得 米, 米, ,在 处测得电线杆顶端 的仰角为 ,则电线杆 的高度约为米.(参考数据: , ,结果按四舍五入保留一位小数)
15. 如图,直立于地面上的电线杆 ,在阳光下落在水平地面和坡面上的影子分别是 、 ,测得 米, 米, ,在 处测得电线杆顶端 的仰角为 ,则电线杆 的高度约为米.(参考数据: , ,结果按四舍五入保留一位小数)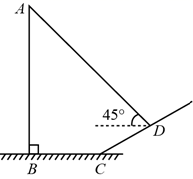 16. 如图,从楼顶 处看楼下荷塘 处的俯角为 ,看楼下荷塘 处的俯角为 ,已知楼高 为 米,则荷塘的宽 为米.(结果保留根号)
16. 如图,从楼顶 处看楼下荷塘 处的俯角为 ,看楼下荷塘 处的俯角为 ,已知楼高 为 米,则荷塘的宽 为米.(结果保留根号)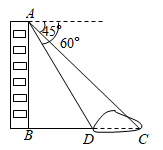 17. 在直角 中, , , 的角平分线交 于点 ,且 ,斜边 的值是.18. 如图,等腰三角形ABC中,AB=AC,BC=6,cos∠ABC= ,点P在边AC上运动(可与点A,C重合),将线段BP绕点P逆时针旋转120°,得到线段DP,连接BD,则BD长的最大值为.
17. 在直角 中, , , 的角平分线交 于点 ,且 ,斜边 的值是.18. 如图,等腰三角形ABC中,AB=AC,BC=6,cos∠ABC= ,点P在边AC上运动(可与点A,C重合),将线段BP绕点P逆时针旋转120°,得到线段DP,连接BD,则BD长的最大值为.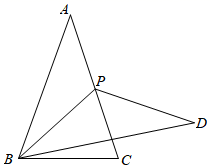
三、解答题
-
19. 计算:(2021﹣π)0﹣|2﹣ |+( )﹣1•tan60°.20. 计算: .21. 有诗云:东山雨霁画屏开,风卷松声入耳来.一座楼阁镇四方,团结一心建家乡.1987年为庆祝湘西自治州成立三十周年,湘西州政府在花果山公园内修建了一座三层楼高的“一心阁”民族团结楼阁.芙蓉学校数学实践活动小组为测量“一心阁” 的高度,在楼前的平地上A处,观测到楼顶 处的仰角为30°,在平地上 处观测到楼顶 处的仰角为 ,并测得A、 两处相距 ,求“一心阁” 的高度.(结果保留小数点后一位,参考数据: , )
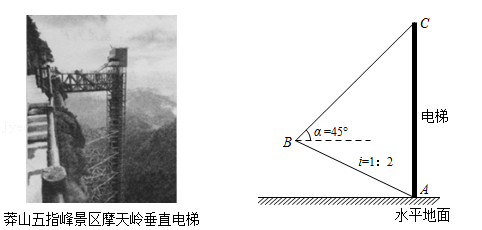
 22. 如图,莽山五指峰景区新建了一座垂直观光电梯.某测绘兴趣小组为测算电梯AC的高度,测得斜坡AB=105米,坡度i=1:2,在B处测得电梯顶端C的仰角α=45°,求观光电梯AC的高度.
22. 如图,莽山五指峰景区新建了一座垂直观光电梯.某测绘兴趣小组为测算电梯AC的高度,测得斜坡AB=105米,坡度i=1:2,在B处测得电梯顶端C的仰角α=45°,求观光电梯AC的高度.(参考数据: ≈1.41, ≈1.73, ≈2.24.结果精确到0.1米)
 23. 在一次课外活动中,某数学兴趣小组测量一棵树 的高度.如图所示,测得斜坡 的坡度 ,坡底 的长为8米,在 处测得树 顶部 的仰角为 ,在 处测得树 顶部 的仰角为 ,求树高 .(结果保留根号)
23. 在一次课外活动中,某数学兴趣小组测量一棵树 的高度.如图所示,测得斜坡 的坡度 ,坡底 的长为8米,在 处测得树 顶部 的仰角为 ,在 处测得树 顶部 的仰角为 ,求树高 .(结果保留根号) 24. 随着科学技术的不断进步,无人机被广泛应用到实际生活中,小星利用无人机来测量广场 两点之间的距离.如图所示,小星站在广场的 处遥控无人机,无人机在 处距离地面的飞行高度是 ,此时从无人机测得广场 处的俯角为 ,他抬头仰视无人机时,仰角为 ,若小星的身高 (点 在同一平面内).
24. 随着科学技术的不断进步,无人机被广泛应用到实际生活中,小星利用无人机来测量广场 两点之间的距离.如图所示,小星站在广场的 处遥控无人机,无人机在 处距离地面的飞行高度是 ,此时从无人机测得广场 处的俯角为 ,他抬头仰视无人机时,仰角为 ,若小星的身高 (点 在同一平面内). (1)、求仰角 的正弦值;(2)、求 两点之间的距离(结果精确到 ).25. 已知,在△ABC中,∠BAC=90°
(1)、求仰角 的正弦值;(2)、求 两点之间的距离(结果精确到 ).25. 已知,在△ABC中,∠BAC=90° (1)、如图1,已知点D在BC边上,∠DAE=90°,连结CE.试探究BD与CE的关系;(2)、如图2,已知点D在BC下方,∠DAE=90°,连结CE.若BD⊥AD,AB=2 ,AD交BC于点F,求AF的长;(3)、如图3,已知点D在BC下方,连结AD、BD、CD.若∠CBD=30°,AB2=6,AD2=4+ ,求sin∠BCD的值.
(1)、如图1,已知点D在BC边上,∠DAE=90°,连结CE.试探究BD与CE的关系;(2)、如图2,已知点D在BC下方,∠DAE=90°,连结CE.若BD⊥AD,AB=2 ,AD交BC于点F,求AF的长;(3)、如图3,已知点D在BC下方,连结AD、BD、CD.若∠CBD=30°,AB2=6,AD2=4+ ,求sin∠BCD的值.