浙江省湖州市三贤联盟2021-2022学年高二上学期数学期中联考试卷

试卷更新日期：2021-11-26 类型：期中考试

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分；

1. 在空间坐标系中，点 $A (1 ， 3 ， - 5)$ 关于 $y$ 轴的对称点为（）

A、 $(1 ， 3 ， 5)$ B、 $(1 ， - 3 ， - 5)$ C、 $(- 1 ， 3 ， 5)$ D、 $(1 ， - 3 ， 5)$

查看试题解析
2. 在平面直角坐标系中，直线 $x + \sqrt{3} y - 3 = 0$ 的斜率是（）

A、 $- \frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $- \sqrt{3}$ D、 $\sqrt{3}$

查看试题解析
3. 已知向量 $\vec{a} = (2 ， - 1 ， 3) ， \vec{b} = (k ， - 2 ， 1)$ ，且 $\vec{a}$ 与 $\vec{b}$ 互相垂直，则k＝（）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、 $- \frac{5}{2}$ D、 $\frac{5}{2}$

查看试题解析
4. “ $m > 0$ 且 $n > 0$ ”是“方程 $m x^{2} + n y^{2} = 1$ 表示椭圆”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件

查看试题解析
5. 已知直线 $x + y + 2 = 0$ 分别与 $x$ 轴、 $y$ 轴交于 $A$ ， $B$ 两点，点 $P$ 在圆 ${(x - 2)}^{2} + y^{2}$ =2上，则 $△ A B P$ 面积的取值范围是（）

A、 $[2 ， 6]$ B、 $[4 ， 8]$ C、 $[\sqrt{2} ， 3 \sqrt{2}]$ D、 $[2 \sqrt{2} ， 3 \sqrt{2}]$

查看试题解析
6. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左右焦点分别为 $F_{1}$ ， $F_{2}$ ，离心率为 $e$ ，若椭圆上存在点 $P$ ，使得 $\frac{P F_{1}}{P F_{2}} = e$ ，则该离心率 $e$ 的取值范围是（）

A、 $(0 ， \sqrt{2} - 1]$ B、 $[\frac{\sqrt{2}}{2} ， 1)$ C、 $[\sqrt{2} - 1 ， 1)$ D、 $(0 ， \frac{\sqrt{2}}{2}]$

查看试题解析
7. 如图，某市有相交于点 $O$ 的一条东西走向的公路 $l$ 与一条南北走向的公路 $m$ ，有一商城 $A$ 的部分边界是椭圆的四分之一，这两条公路为椭圆的对称轴，椭圆的长半轴长为2，短半轴长为1（单位：千米）．根据市民建议，欲新建一条公路 $P Q$ ，点 $P$ ， $Q$ 分别在公路 $m$ ， $l$ 上，且要求 $P Q$ 与椭圆形商城 $A$ 相切，当公路 $P Q$ 长最短时， $O Q$ 的长为（）

A、 $\sqrt{2}$ B、 $2 \sqrt{2}$ C、 $\sqrt{3}$ D、 $\sqrt{6}$

查看试题解析
8. 在三棱锥 $S - A B C$ 中， $S A ， S B ， S C$ 两两垂直且相等，若空间中动一点 $P$ 满足 $\vec{S P} = x \vec{S A} + y \vec{S B} + z \vec{S C}$ ，其中 $x \geq 0 ， y \geq 1 ， z \geq 1$ 且 $x + y + z \leq \frac{12}{5}$ .记 $S P$ 与平面 $A B C$ 所成的角为 $θ$ ，则 $\sin θ$ 的最大值（）

A、 $\frac{1}{3}$ B、 $\frac{2 \sqrt{2}}{3}$ C、1 D、 $\frac{4 \sqrt{66}}{33}$

查看试题解析

二、选择题：本题共4小题，每小题5分，共20分；在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，有选错的得0分，部分选对的得3分.

9. 已知直线 $l$ 经过点 $(- 4 ， \sqrt{3})$ ，且直线 $l$ 的一个方向向量为 $\vec{n} = (\sqrt{3} ， - 1)$ ，则下列结论中正确的是（）

A、 $l$ 在 $x$ 轴上的截距为 $- 1$ B、 $l$ 的倾斜角等于120º C、 $l$ 与直线 $y = \sqrt{3} x + 2$ 垂直 D、向量 $\vec{n_{1}} = (- 1 ， - \sqrt{3})$ 为直线的一个法向量

查看试题解析
10. 若 $P$ ， $Q$ 分别为 $l_{1} ： 3 x + 4 y + 5 = 0$ ， $l_{2} ： a x + 8 y + c = 0$ 上的动点，且 $l_{1}$ ∥ $l_{2}$ ，下面说法正确的有（）

A、直线 $l_{2}$ 的斜率为定值 B、当 $c = 25$ 时， $| P Q |$ 的最小值为 $\frac{3}{2}$ C、当 $| P Q |$ 的最小值为1时， $c = 20$ D、 $c \neq 10$

查看试题解析
11. 直线 $y = x + b$ 与曲线 $x = \sqrt{1 - y^{2}}$ 恰有一个交点，实数 $b$ 可取下列哪些值（）

A、 $- \sqrt{2}$ B、-1 C、1 D、 $\sqrt{2}$

查看试题解析
12. 在正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B = A A_{1} = 1$ ，点 $P$ 满足 $\vec{B P} = λ \vec{B C} + μ \vec{B B_{1}}$ ，其中 $λ \in [0 ， 1]$ ， $μ \in [0 ， 1]$ ，则（）

A、当 $λ = 1$ 时， $△ A B_{1} P$ 的周长为定值 B、当 $μ = 1$ 时，三棱锥 $P - A_{1} B C$ 的体积为定值 C、当 $λ = \frac{1}{2}$ 时，有且仅有一个点 $P$ ，使得 $A_{1} P ⊥ B P$ D、当 $μ = \frac{1}{2}$ 时，有且仅有一个点 $P$ ，使得 $A_{1} B ⊥$ 平面 $A B_{1} P$

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分.

13. 已知向量 $\vec{a} = (2 ， - 1 ， 3)$ ， $\vec{b} = (- 1 ， 4 ， - 2)$ ， $\vec{c} = (3 ， 2 ， λ)$ ，若 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ 共面，则实数 $λ$ ＝.

查看试题解析
14. 过点 $(\sqrt{3} ， - 1)$ 作圆 $x^{2} + y^{2} = 4$ 的切线，则切线的方程为.

查看试题解析
15. 经过椭圆 $\frac{x^{2}}{2} + y^{2} = 1$ 的左焦点 $F_{1}$ 作倾斜角为60º的直线 $l$ ，直线 $l$ 与椭圆相交于 $A ， B$ 两点，则线段 $A B$ 的长为．

查看试题解析
16. 舒腾尺是荷兰数学家舒腾（1615-1660）设计的一种作图工具，如图， $O$ 是滑槽 $A B$ 的中点，短杆 $O N$ 可绕 $O$ 转动，长杆 $M N$ 通过 $N$ 处的铰链与 $O N$ 连接， $M N$ 上的栓子 $D$ 可沿滑槽 $A B$ 滑动.当点 $D$ 在滑槽 $A B$ 内作往复移动时，带动点 $N$ 绕 $O$ 转动，点 $M$ 也随之而运动.记点 $N$ 的运动轨迹为 $C_{1}$ ，点 $M$ 的运动轨迹为 $C_{2}$ .若 $O N = D N = 1$ ， $M N = 3$ ，过 $C_{2}$ 上的点 $P$ 向 $C_{1}$ 作切线，则切线长的最大值为．

查看试题解析

四、解答题：本题共6小题，共70分.

17. 如图，在平行六面体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = A D = A A_{1} = 1 ， ∠ B A D = 60^{°}$ ， $∠ B A A_{1} = ∠ D A A_{1} = 45^{°}$ .

求：(Ⅰ) $\vec{A B} \cdot \vec{A D}$ ；

(Ⅱ) $A C_{1}$ 的长.

查看试题解析
18. 已知直线 $l$ 经过点 $P (4 ， 6)$ .
（Ⅰ）当 $l$ 在两坐标轴上的截距相等时，求 $l$ 的方程；

（Ⅱ）若 $l$ 与 $x$ 轴、 $y$ 轴的正半轴分别相交于 $A$ 、 $B$ 两点，当三角形 $A O B$ 的面积最小时，求 $l$ 的方程.

查看试题解析
19. 如图所示，某隧道内设双行线公路，其截面由一段圆弧和一个长方形的三边构成．已知隧道总宽度 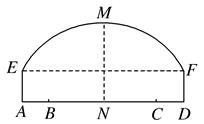$A D$ 为 $6 \sqrt{3} m$ ，行车道总宽度 $B C$ 为 $2 \sqrt{11} m$ ，侧墙高 $E A$ ， $F D$ 为 $2 m$ ，弧顶高 $M N$ 为 $5 m$ .

(Ⅰ)以 $E F$ 所在直线为 $x$ 轴， $M N$ 所在直线为 $y$ 轴， $1 m$ 为单位长度建立平面直角坐标系，求圆弧所在的圆的标准方程；

(Ⅱ)为保证安全，要求隧道顶部与行驶车辆顶部(设为平顶)在竖直方向上的高度之差至少为 $0.5 m$ ，问车辆通过隧道的限制高度是多少？

查看试题解析
20. 已知直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，侧面 $A A_{1} B_{1} B$ 为正方形， $A B = B C = 2$ ，E ， F分别为 $A C$ 和 $C C_{1}$ 的中点，D为棱 $A_{1} B_{1}$ 上的点， $B F ⊥ A_{1} B_{1}$ ．
（Ⅰ）证明： $B F ⊥ D E$ ；

（Ⅱ）当 $B_{1} D$ 为何值时，面 $B B_{1} C_{1} C$ 与面 $D F E$ 所成的二面角的正弦值最小?

查看试题解析
21. 已知两个定点 $A (0 ， 4)$ ， $B (0 ， 1)$ ，动点 $P$ 满足 $| P A | = 2 | P B |$ ，设动点 $P$ 的轨迹为曲线 $E$ ，直线 $l ： y = x - 4$ .
（Ⅰ）求曲线 $E$ 的轨迹方程；

（Ⅱ）若 $Q$ 是直线 $l$ 上的动点，过 $Q$ 作曲线 $E$ 的两条切线 $Q M$ ， $Q N$ ，切点为 $M$ ， $N$ ，探究：直线 $M N$ 是否过定点，若有，请求出定点，否则说明理由．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，过椭圆 $M ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $(a > b > 0)$
右焦点的直线 $x + y - \sqrt{3} = 0$ 交 $M$ 于 $A$ ， $B$ 两点， $P$ 为 $A B$ 的中点，且 $O P$ 的斜率为 $\frac{1}{2}$ .

（Ⅰ）求椭圆 $M$ 的方程；

（Ⅱ）已知 $C$ ， $D$ 为 $M$ 上的两点，若四边形 $A C B D$ 的对角线 $C D ⊥ A B$ ，求四边形 $A C B D$ 面积的最大值.

查看试题解析