湖南省永州市2021-2022学年高三上学期数学第一次适应性考试试卷
试卷更新日期:2021-11-26 类型:月考试卷
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 若复数z (i是虚数单位),则|z|=( )A、 B、 C、1 D、3. 过圆 的圆心且与直线 垂直的直线方程为( )A、 B、 C、 D、4. 永州是一座有着两千多年悠久历史的湘南古邑,民俗文化资源丰富.在一次民俗文化表演中,某部门安排了《东安武术》、《零陵渔鼓》、《瑶族伞舞》、《祁阳小调》、《道州调子戏》、《女书表演》六个节目,其中《祁阳小调》与《道州调子戏》不相邻,则不同的安排种数为( )A、480 B、240 C、384 D、14405. 已知 , , 是三个不同的平面, , 是两条不同的直线,下列命题为真命题的是( )A、若 , ,则 B、若 , ,则 C、若 , ,则 D、若 , ,则6. 在数列 中, ,则 ( )A、25 B、32 C、62 D、727. 若 ,则 ( )A、-5 B、-3 C、3 D、58. 已知函数 是定义在 上的偶函数,且 为奇函数.若 ,则曲线 在点 处的切线方程为( )A、 B、 C、 D、9. “直播电商”已经成为当前经济发展的新增长点,某电商平台的直播间经营化妆品和服装两大类商品,2020年前三个季度,该直播间每个季度的收入都比上一季度的收入翻了一番,其前三季度的收入情况如图所示,则( )
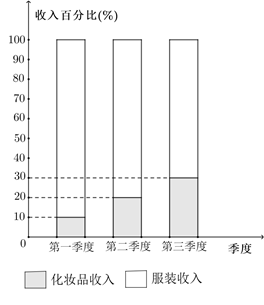 A、该直播间第三季度总收入是第一季度总收入的3倍 B、该直播间第二季度化妆品收入是第三季度化妆品收入的 C、该直播间第一季度化妆品收入是第三季度化妆品收入的 D、该直播间第三季度服装收入高于前两个季度的服装收入之和
A、该直播间第三季度总收入是第一季度总收入的3倍 B、该直播间第二季度化妆品收入是第三季度化妆品收入的 C、该直播间第一季度化妆品收入是第三季度化妆品收入的 D、该直播间第三季度服装收入高于前两个季度的服装收入之和二、多选题
-
10. 已知函数 ,则 在区间 上为减函数的充分条件是( )A、 B、 的图象关于直线 对称 C、 是奇函数 D、 的图象关于点 对称11. 已知 为坐标原点, 、 分别为双曲线 的左、右焦点,点 在双曲线的右支上,则( )A、当 时,双曲线的离心率 B、当 是面积为2的正三角形时, C、当 为双曲线的右顶点, 轴时, D、当射线 与双曲线的一条渐近线交于点 时,12. 已知函数 ,则( )A、当 , 时, B、当 时, 有最值 C、当 时, 为减函数 D、当 仅有一个整数解时,
三、填空题
-
13. 已知 , , ,则 .14. 设 , , ,则 , , 从小到大的顺序为.15. 已知抛物线 : ,过焦点 作倾斜角为 的直线与 交于 , 两点, , 在 的准线上的投影分别为 , 两点,则 .16. 长方体 中, , ,点 满足 ,其中 , .若 ,则三棱锥 的体积为;若 为 的中点,且 ,则点 的轨迹与长方体的侧面 的交线长为.
四、解答题
-
17. 已知数列 满足 , .(1)、求 ;(2)、记 ,证明:数列 为等比数列.18. 如图,四边形 为平行四边形, ,四边形 为矩形,且 平面 , .
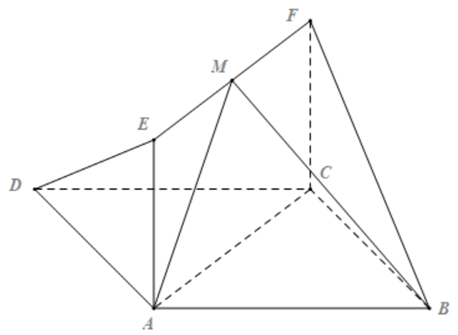 (1)、证明:平面 平面 ;(2)、若 为 的中点,求平面 与平面 所成锐二面角的余弦值.19. 如图,在平面四边形 中, , , , .
(1)、证明:平面 平面 ;(2)、若 为 的中点,求平面 与平面 所成锐二面角的余弦值.19. 如图,在平面四边形 中, , , , .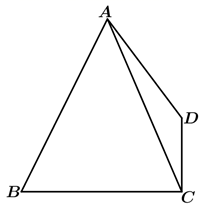 (1)、求 ;(2)、若 为锐角三角形,求 面积的取值范围.20. 某校积极响应习近平总书记关于共建学习型社会的号召,开展了“学党史,强信仰,跟党走”的主题学习活动.在一次“党史”知识竞赛活动中,给出了 、 、 三道题,答对 、 、 分别得2分、2分、4分,答错不得分.已知甲同学答对问题 、 、 的概率分别为 、 、 ,乙同学答对问题 、 、 的概率均为 ,甲、乙两位同学都需回答这三道题,且各题回答正确与否相互独立.(1)、求甲同学至少有一道题不能答对的概率;(2)、请结合统计的知识判断甲、乙两人在本次“党史”知识竞赛中,哪位同学得分高.
(1)、求 ;(2)、若 为锐角三角形,求 面积的取值范围.20. 某校积极响应习近平总书记关于共建学习型社会的号召,开展了“学党史,强信仰,跟党走”的主题学习活动.在一次“党史”知识竞赛活动中,给出了 、 、 三道题,答对 、 、 分别得2分、2分、4分,答错不得分.已知甲同学答对问题 、 、 的概率分别为 、 、 ,乙同学答对问题 、 、 的概率均为 ,甲、乙两位同学都需回答这三道题,且各题回答正确与否相互独立.(1)、求甲同学至少有一道题不能答对的概率;(2)、请结合统计的知识判断甲、乙两人在本次“党史”知识竞赛中,哪位同学得分高.