浙江省诸暨市2021-2022学年八年级上学期数学期中阶段性测试试卷

试卷更新日期：2021-11-26 类型：期中考试

进入 出卷网 下载

一、选择题（本大题共10小题，每小题3分，共30分.）

  • 1. 下列图标中轴对称图形的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 已知三角形的一边长为8，则它的另两边长分别可以是（   ）
    A、2，9 B、17，29 C、3，12 D、4，4

    查看试题解析

  • 3. 已知图中的两个三角形全等，则∠α等于（   ）

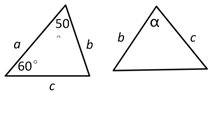    A、50° B、60° C、70° D、80°

    查看试题解析

  • 4. 画△ABC的边BC上的高，下列画法正确的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 5. 在说明命题“若a2>b2 ， 则a>b”是假命题时，可以成为反例的是（     ）
    A、a=3， b=2 B、a=3， b= -2 C、a= -1， b= -1 D、a= -3， b=2

    查看试题解析

  • 6. 下列条件中，不能判定两个三角形全等的是（   ）
    A、有一个锐角相等和一组边相等的直角三角形 B、底边和底边上高线对应相等的等腰三角形 C、顶角和底边相等的等腰三角形 D、一条直角边和一条斜边对应相等的直角三角形

    查看试题解析

  • 7. 人字梯中间一般会设计一”拉杆”，这样做的道理是（ ）．

    A、两点之间，线段最短 B、垂线段最短 C、两直线平行，内错角相等 D、三角形具有稳定性

    查看试题解析

  • 8. 在△ABC中，有下列条件：不能确定△ABC是直角三角形的条件是（   ）
    A、∠A+∠B=∠C； B、∠A：∠B：∠C=1：2：3； C、∠A=2∠B=3∠C； D、∠A=∠B=∠

    查看试题解析

  • 9. 如图，在数轴上，点A，B表示的数分别为0，2，BC⊥AB于点B，且BC=1．连接AC，在AC上截取CD=BC，以点A为圆心，AD的长为半径画弧，交线段AB于点E，则点E表示的实数是（   ）

    A、25 B、5+1 C、2 D、5−1

    查看试题解析

  • 10. 如图是一个6×6的正方形网格，每个小正方形的顶点都是格点，等腰△ABC的顶点都是图中的格点，其中点A、点B的位置如图所示，则点C可能的位置共有（   ）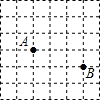

    A、10个 B、9个 C、8个 D、7个

    查看试题解析

二、填空题（本大题有6小题，每小题3分，共18分）

  • 11. 直角三角形的两条直角边为6和8，则斜边上的中线长是 ．

    查看试题解析

  • 12. 如图，∠A＝20°，∠B＝40°，∠C＝50°，则∠ADB的度数是 ．

    查看试题解析

  • 13. 如图所示，已知BE⊥AD，CF⊥AD，垂足分别为E，F，则在下列条件中选择一组，可以判定Rt△ABE≌Rt△DCF的是（填入序号）

    ①AB＝DC，∠B＝∠C；②AB＝DC，AB∥CD；③AB＝DC，BE＝CF；④AB＝DF，BE＝CF．

    查看试题解析

  • 14. 如图，△ABC是直角三角形，AB是斜边，AC＝3，AB＝5，AB的垂直平分线分别交BC，AB于D，E，则BD的长为 ．

    查看试题解析

  • 15. 定义：到三角形两边距离相等的点叫做三角形的准内心．已知在Rt△ABC中，∠C=90°，AC=6，BC=8，点P是△ABC的准内心（不包括顶点），且点P在△ABC的边上，则CP的长为 ．

    查看试题解析

  • 16. 如图，有两条公路OM，ON相交成30°，沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学，当拖拉机沿ON方向行驶时，路两旁50米内会受到噪音影响，已知有两台相距30米的拖拉机正沿ON方向行驶，它们的速度均为5米/秒，问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是秒.

    查看试题解析

三、 解答题(本大题有7小题，共52分.)

  • 17. 如图，已知AD＝AB，AC＝AE，∠DAB＝∠CAE，连接DC，BE．

    (1)、求证：△BAE≌△DAC；
    (2)、若∠CAD＝125°，∠D＝20°，求∠E的度数．

    查看试题解析

  • 18. 如图所示，在△ABC中，BE平分∠ABC，DE∥BC．

    (1)、求证：△BDE是等腰三角形；
    (2)、若∠A＝35°，∠C＝70°，求∠BDE的度数．

    查看试题解析

  • 19. 如图，P是等边三角形ABC内的一点，连结PA，PB，PC，以BP为边作∠PBQ＝60°，且BP＝BQ，连结CQ．

    (1)、观察并猜想AP与CQ之间的大小关系，并说明理由．
    (2)、若PA＝PC＝1，PB＝ 2 ，求证：PC⊥CQ．

    查看试题解析

  • 20. 如图，在一条东西向的马路上有广场A和医院C，在各自正北方向上分别有汽车站B和汽车站D，已知AC=14km，AB=4km，CD=8km.，市政府打算在马路AC段之间建造一个加油站P.

    图1                          图2

    (1)、若要使得加油站P到两汽车站的距离之和最小，请用尺规作图在图1中作出加油站P的位置，并直接写出此时的最小值. （作图请保留痕迹，结果可以保留根号）
    (2)、若要使得加油站到两汽车站的距离相等，请用尺规作图在图2中作出加油站P的位置，并求出此时PA的距离.（作图请保留痕迹）

    查看试题解析

  • 21. 已知，DA，DB，DC是从点D出发的三条线段，且DA＝DB＝DC．

    (1)、如图①，若点D在线段AB上，连接AC，BC，试判断△ABC的形状，并说明理由．
    (2)、如图②，连接AC，BC，AB，且AB与CD相交于点E，若AC＝BC，AB＝16，DC＝10，求CE和AC的长．

    查看试题解析

  • 22. 已知Rt△ABC中∠C=90°，且BC=9，∠B=30°.

        

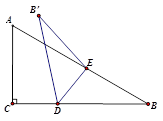
              图1                 图2                      图3

    (1)、如图1、2，若点D是CB上一点，且CD=3，点E是AB上的动点，将△DBE沿DE对折，点B的对应点为B’（点B’和点C在直线AB的异侧），DB’与AB交于点H.

    ①当∠B’EA=20°时，求∠EDB的度数.

    ②当△B’HE是等腰三角形时，求∠DEB的度数.

    (2)、如图2，若点D是CB上一点，且CD=3，M是线段AC上的动点，以∠MDN为直角构造等腰直角△DMN（D，M，N三点顺时针方向排列），在点M的运动过程中，直接写出CN+NB的最小值.

    查看试题解析