重庆市江津区师大附中等金砖四校2021-2022学年八年级上学期数学期中考试试卷
试卷更新日期:2021-11-26 类型:期中考试
一、单选题
-
1. 列四个图案中,不是轴对称图案的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的三根小木棒能构成三角形的是( )A、2cm,3cm,5cm B、7cm,4cm,2cm C、3cm,4cm,8cm D、3cm,3cm,4cm3. 等腰三角形的一个内角为50°,则另外两个角的度数分别为( )A、65°,65° B、50°,80° C、65°,65°或50°,80° D、50°,50°4. 如图,给出下列四组条件:
2. 下列长度的三根小木棒能构成三角形的是( )A、2cm,3cm,5cm B、7cm,4cm,2cm C、3cm,4cm,8cm D、3cm,3cm,4cm3. 等腰三角形的一个内角为50°,则另外两个角的度数分别为( )A、65°,65° B、50°,80° C、65°,65°或50°,80° D、50°,50°4. 如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;
②AB=DE,∠B=∠E.BC=EF;
③∠B=∠E,BC=EF,∠C=∠F;
④AB=DE,AC=DF,∠B=∠E.
其中,能使△ABC≌△DEF的条件共有( )
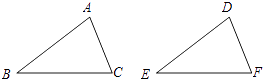 A、1组 B、2组 C、3组 D、4组5. 已知点 关于原点对称的点在第四象限,则 的取值范围在数轴上表示正确的是( )A、
A、1组 B、2组 C、3组 D、4组5. 已知点 关于原点对称的点在第四象限,则 的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( ) .
6. 如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( ) .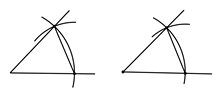 A、SAS B、ASA C、AAS D、SSS7. 小明每走5米,顺时针转20°,则( )A、小明不会回到原点 B、小明会回到原点,路程小于80m C、小明会回到原点,路程恰为90m D、小明会回到原点,路程大于120m8. 如图,在 中, ,若沿图中虚线截去 ,则 ( )
A、SAS B、ASA C、AAS D、SSS7. 小明每走5米,顺时针转20°,则( )A、小明不会回到原点 B、小明会回到原点,路程小于80m C、小明会回到原点,路程恰为90m D、小明会回到原点,路程大于120m8. 如图,在 中, ,若沿图中虚线截去 ,则 ( ) A、150° B、200° C、210° D、240°9. 如图在 中, 平分 交 于 , 于 ,若 ,则 的周长是( )
A、150° B、200° C、210° D、240°9. 如图在 中, 平分 交 于 , 于 ,若 ,则 的周长是( )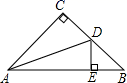 A、 B、 C、 D、10. 如图,△ABC的面积为1cm2 , AP垂直∠B的平分线BP于P,则△PBC的面积为( )
A、 B、 C、 D、10. 如图,△ABC的面积为1cm2 , AP垂直∠B的平分线BP于P,则△PBC的面积为( ) A、0.4 cm2 B、0.5 cm2 C、0.6 cm2 D、0.7 cm211. 如图,等腰三角形ABC的底边BC长为3,面积是18,腰AC的垂直平分线EF分别交AC,AB边于E, F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
A、0.4 cm2 B、0.5 cm2 C、0.6 cm2 D、0.7 cm211. 如图,等腰三角形ABC的底边BC长为3,面积是18,腰AC的垂直平分线EF分别交AC,AB边于E, F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( ) A、7.5 B、8.5 C、10.5 D、13.512. 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的有( )个①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.
A、7.5 B、8.5 C、10.5 D、13.512. 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的有( )个①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH. A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 等腰△ABC的两边长分别为2和5,则第三边长为.14. 如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若△ADE的周长为9,△ABC的周长是14,则BC=.
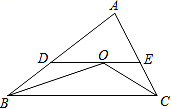 15. 如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AC,垂足为E,∠BAC=56°,则∠ADE的度数是.
15. 如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AC,垂足为E,∠BAC=56°,则∠ADE的度数是. 16. 等腰三角形一腰上的高与另一腰的夹角为36°,则该等腰三角形的底角的度数为 .17. 如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高.若AB+AC=8,S△ABC=24,∠EDF=120°,则AD的长为 .
16. 等腰三角形一腰上的高与另一腰的夹角为36°,则该等腰三角形的底角的度数为 .17. 如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高.若AB+AC=8,S△ABC=24,∠EDF=120°,则AD的长为 . 18. 如图,在△ABC中,∠BAC=80°,DE,FG分别是AB,AC边的垂直平分线,点E、F在BC上,则∠FAE的度数为.
18. 如图,在△ABC中,∠BAC=80°,DE,FG分别是AB,AC边的垂直平分线,点E、F在BC上,则∠FAE的度数为.
三、解答题
-
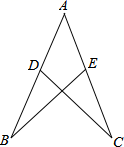
19. 如图,点D在 上,点E在 上, , ,求证: .
 20. 如图,AD是△ABC的BC边上的高,若∠B=42°,∠C=72°.
20. 如图,AD是△ABC的BC边上的高,若∠B=42°,∠C=72°. (1)、求作AE平分∠BA C交BC于点E.(尺规作图,保留作图痕迹,不写作法.)(2)、求∠DAE的度数.21. 如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)、求作AE平分∠BA C交BC于点E.(尺规作图,保留作图痕迹,不写作法.)(2)、求∠DAE的度数.21. 如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O. (1)、求证:△AEC≌△BED;(2)、若∠1=42°,求∠BDE的度数.22. △ABC在平面直角坐标系中的位置如图所示A、B、C三点在格点上.
(1)、求证:△AEC≌△BED;(2)、若∠1=42°,求∠BDE的度数.22. △ABC在平面直角坐标系中的位置如图所示A、B、C三点在格点上.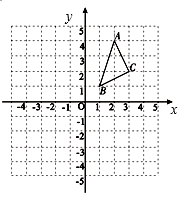 (1)、作出△ABC关于x轴对称的△A1B1C1 , 并写出点C1的坐标;(2)、作出△ABC关于y对称的△A2B2C2 , 并写出点C2的坐标.(3)、求△ABC的面积.23. 如图,已知点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.
(1)、作出△ABC关于x轴对称的△A1B1C1 , 并写出点C1的坐标;(2)、作出△ABC关于y对称的△A2B2C2 , 并写出点C2的坐标.(3)、求△ABC的面积.23. 如图,已知点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.
求证:
(1)、△ABC≌△DEF;
(2)、BE=CF
24. 如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.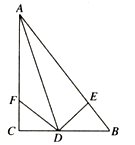 (1)、求证:CF=EB.(2)、若AB=12,AF=8,求CF的长.25. 若一个两位自然数m= (x,y为整数,且1≤x≤9,1≤y≤9),将十位数字的平方、十位数字,个位数字与十位数字的乘积从左到右依次组成一个新数 ,称 为m的“新鲜数”. 例如:m=35,其十位上数字的平方及十位数字与两个数位上数字的乘积分别为:9、3、15,则35的“新鲜数”为9315.(1)、46的“新鲜数”为 , m的“新鲜数”为9324,则m=;(2)、设 (1≤a≤3,且a为整数),记它的“新鲜数”为q,在q的十位和个位之间插入一个数字 ,得到一个新数t,若t恰好被4整除,求符合条件的所有t值.26. 已知△ABC中,∠ABC=90°,AB=BC,点A、B分别是x轴和y轴上的一动点.
(1)、求证:CF=EB.(2)、若AB=12,AF=8,求CF的长.25. 若一个两位自然数m= (x,y为整数,且1≤x≤9,1≤y≤9),将十位数字的平方、十位数字,个位数字与十位数字的乘积从左到右依次组成一个新数 ,称 为m的“新鲜数”. 例如:m=35,其十位上数字的平方及十位数字与两个数位上数字的乘积分别为:9、3、15,则35的“新鲜数”为9315.(1)、46的“新鲜数”为 , m的“新鲜数”为9324,则m=;(2)、设 (1≤a≤3,且a为整数),记它的“新鲜数”为q,在q的十位和个位之间插入一个数字 ,得到一个新数t,若t恰好被4整除,求符合条件的所有t值.26. 已知△ABC中,∠ABC=90°,AB=BC,点A、B分别是x轴和y轴上的一动点. (1)、如图1,若点A(3,0),B(0,﹣1),求点C的坐标;(2)、如图2,分别以OB、AB为直角边在第三、四象限作等腰直角△OBF和等腰直角△ABE,EF交y轴于M,若S△BEM=6,求S△ABO.
(1)、如图1,若点A(3,0),B(0,﹣1),求点C的坐标;(2)、如图2,分别以OB、AB为直角边在第三、四象限作等腰直角△OBF和等腰直角△ABE,EF交y轴于M,若S△BEM=6,求S△ABO.