浙江省金华市2021-2022学年八年级上学期数学期中考试试卷
试卷更新日期:2021-11-26 类型:期中考试
一、单选题
-
1. 中国汉字文化博大精深,蕴含了古人的智慧,其中也包含了数学的韵味,在下列文字中,可以将其看成轴对称图形的文字是( )A、“最” B、“美” C、“东” D、“阳”2. 若 ,则下列不等式不一定成立的是( )A、 B、 C、 D、3. 若 三边长 , , 满足 , 是( )A、直角三角形 B、等腰三角形 C、等边三角形 D、等腰直角三角形4. 下列命题中,①在同一平面内,若 a⊥b , ,则 ;②相等的角是对顶角;③能被2整除的数也能被4整除;④两点之间线段最短.真命题有( )A、1个 B、2个 C、3个 D、4个5. 如图,为了让电线杆垂直于地面,工程人员的操作方法是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,EC在同一直线上时,电线杆DE就垂直于BC工程人员这种操作方法的依据是( )
 A、等边对等角 B、等角对等边 C、垂线段最短 D、等腰三角形“三线合一”6. 如图,一块玻璃碎成三片,小智只带了第③块去玻璃店,就能配一块一模一样的玻璃,你能用三角形的知识解释,这是为什么?( )
A、等边对等角 B、等角对等边 C、垂线段最短 D、等腰三角形“三线合一”6. 如图,一块玻璃碎成三片,小智只带了第③块去玻璃店,就能配一块一模一样的玻璃,你能用三角形的知识解释,这是为什么?( ) A、 B、 C、 D、7. 关于 的两个代数式 与 的值的符号相反,则 的取值范围是( )A、 B、 C、 D、 或8. 如图,给你一张锐角三角形纸片,请你用折叠的方式,折出过点 的角平分线、中线、高线,能成功折出的是( )
A、 B、 C、 D、7. 关于 的两个代数式 与 的值的符号相反,则 的取值范围是( )A、 B、 C、 D、 或8. 如图,给你一张锐角三角形纸片,请你用折叠的方式,折出过点 的角平分线、中线、高线,能成功折出的是( ) A、角平分线 B、中线 C、高线 D、都可以9. 如图,网格线的交点称为格点,任取 个格点构成等腰三角形,则下列可以作为腰长的是( )
A、角平分线 B、中线 C、高线 D、都可以9. 如图,网格线的交点称为格点,任取 个格点构成等腰三角形,则下列可以作为腰长的是( ) A、 B、 C、 D、10. 小李同学在学习“2.7探索勾股定理”时发现,公式 中的 、 、 可以看成以 、 、 为边的正方形面积,利用面积之间的等量关系 ,验证了勾股定理,他对这个发现进一步进行思考,如果分别以这三边向外构造等边三角形、等腰直角三角形、等腰三角形( 、 、 为底)、半圆,其中不满足 这个关系的是( )A、
A、 B、 C、 D、10. 小李同学在学习“2.7探索勾股定理”时发现,公式 中的 、 、 可以看成以 、 、 为边的正方形面积,利用面积之间的等量关系 ,验证了勾股定理,他对这个发现进一步进行思考,如果分别以这三边向外构造等边三角形、等腰直角三角形、等腰三角形( 、 、 为底)、半圆,其中不满足 这个关系的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. “x与4的和小于10”用不等式表示为.12. 如图,在 中, , ,点 在 的延长线上,则 等于 .
 13. “直角三角形的两个锐角互余”的逆命题是命题 填“真”或“假” .14. 如图, 是 的中线,把 沿着直线 对折,点 落在点 处.如果 ,则 .
13. “直角三角形的两个锐角互余”的逆命题是命题 填“真”或“假” .14. 如图, 是 的中线,把 沿着直线 对折,点 落在点 处.如果 ,则 . 15. 如果等腰三角形的三边均为整数,且底边长度比腰长大 ,周长不超过 ,那么的底边长为 .16. 如图, 是 的角平分线,点 是 上的动点,已知 , , ,则(1)、 ;(2)、 的最小值是.
15. 如果等腰三角形的三边均为整数,且底边长度比腰长大 ,周长不超过 ,那么的底边长为 .16. 如图, 是 的角平分线,点 是 上的动点,已知 , , ,则(1)、 ;(2)、 的最小值是.
三、解答题
-
17. 解下列不等式(组):(1)、(2)、18. 如图,在方格中,按下列要求画三角形,使它的顶点均在方格的顶点上(小正方形边长为 )
 (1)、在图1中画一个三角形与 全等,且有一条公共边;(2)、在图2中画一个面积为 的等腰直角三角形.19. 等腰三角形的一边长等于6cm,周长等于28cm,求其他两边的长.20. 如图,在 中, , 的角平分线交 于点 ,过点 作 交 的延长线于点 .
(1)、在图1中画一个三角形与 全等,且有一条公共边;(2)、在图2中画一个面积为 的等腰直角三角形.19. 等腰三角形的一边长等于6cm,周长等于28cm,求其他两边的长.20. 如图,在 中, , 的角平分线交 于点 ,过点 作 交 的延长线于点 .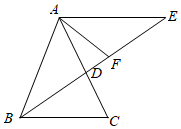 (1)、若 ,求 的度数.(2)、若 是 上的一点,且 , 与 相等吗?请说明理由.21. 对 , 定义一种新运算 (中 , 均为非零常数).例如: ;已知 , .(1)、求 , 的值;(2)、若关于 的不等式组 恰好只有 个整数解,求 的取值范围.22. 如图: 是等腰三角形,
(1)、若 ,求 的度数.(2)、若 是 上的一点,且 , 与 相等吗?请说明理由.21. 对 , 定义一种新运算 (中 , 均为非零常数).例如: ;已知 , .(1)、求 , 的值;(2)、若关于 的不等式组 恰好只有 个整数解,求 的取值范围.22. 如图: 是等腰三角形, (1)、若 ,请你将三角形 分成两个等腰三角形,画一画,并标出各角的度数.(2)、若剪一刀,能将分割成两个等腰三角形,则 度数是多少?(直接写出答案)23. 接种新冠病毒疫苗,建立全民免疫屏障,是战胜病毒的重要手段.北京科兴中维需运输一批疫苗到我市疾控中心,据调查得知,2辆 型冷链运输车与3辆 型冷链运输车一次可以运输600盒:5辆 型冷链运输车与6辆 型冷链运输车一次可以运输1350盒.(1)、求每辆 型车和每辆 型车一次可以分别运输多少盒疫苗.(2)、计划用两种冷链运输车共12辆运输这批疫苗, 型车一次需费用5000元, 型车一次需费用3000元.若运输物资不少于1500盒,且总费用小于54000元.请你列出所有运输方案,并指出哪种方案所需费用最少,最少费用是多少?24. 如图, 是等腰直角三角形, , ,点 是线段 上的一个动点,连接 ,将线段 绕 点顺时针旋转 至点 ,连接 交 于点 .
(1)、若 ,请你将三角形 分成两个等腰三角形,画一画,并标出各角的度数.(2)、若剪一刀,能将分割成两个等腰三角形,则 度数是多少?(直接写出答案)23. 接种新冠病毒疫苗,建立全民免疫屏障,是战胜病毒的重要手段.北京科兴中维需运输一批疫苗到我市疾控中心,据调查得知,2辆 型冷链运输车与3辆 型冷链运输车一次可以运输600盒:5辆 型冷链运输车与6辆 型冷链运输车一次可以运输1350盒.(1)、求每辆 型车和每辆 型车一次可以分别运输多少盒疫苗.(2)、计划用两种冷链运输车共12辆运输这批疫苗, 型车一次需费用5000元, 型车一次需费用3000元.若运输物资不少于1500盒,且总费用小于54000元.请你列出所有运输方案,并指出哪种方案所需费用最少,最少费用是多少?24. 如图, 是等腰直角三角形, , ,点 是线段 上的一个动点,连接 ,将线段 绕 点顺时针旋转 至点 ,连接 交 于点 . (1)、连接 ,求证: ;(2)、当 时,判断 是什么三角形?并说明理由;(3)、在点 运动过程中,当 是锐角三角形时,求 的取值范围.
(1)、连接 ,求证: ;(2)、当 时,判断 是什么三角形?并说明理由;(3)、在点 运动过程中,当 是锐角三角形时,求 的取值范围.