广西壮族自治区河池市凤山县2021-2022学年八年级上学期数学期中考试试卷
试卷更新日期:2021-11-26 类型:期中考试
一、单选题
-
1. 以下列各组线段为边,能组成三角形的是( )A、2cm,3cm,5cm B、3cm,3cm,6cm C、5cm,8cm,2cm D、4cm,5cm,6cm2. 下列说法正确的是( )A、形状相同的两个三角形全等 B、面积相等的两个三角形全等 C、完全重合的两个三角形全等 D、所有的等边三角形全等3. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
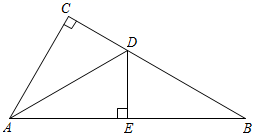
D、 4. 若点 关于 轴对称,则 的值分别为( )A、 ,3 B、 C、7,3 D、7,5. 具备下列条件的四个三角形中,不是直角三角形的是( )A、 B、 C、 D、6. 在下图中,正确画出AC边上高的是( )A、
4. 若点 关于 轴对称,则 的值分别为( )A、 ,3 B、 C、7,3 D、7,5. 具备下列条件的四个三角形中,不是直角三角形的是( )A、 B、 C、 D、6. 在下图中,正确画出AC边上高的是( )A、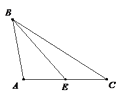 B、
B、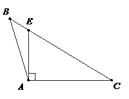 C、
C、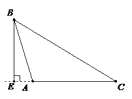 D、
D、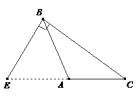 7. 等腰三角形的两边长分别是 和 ,则它的周长是( )A、 B、 C、 或 D、以上都不对8. 到三角形的三边距离相等的点是( )A、三角形三条高的交点 B、三角形三个内角平分线的交点 C、三角形三条中线的交点 D、三角形三边的垂直平分线的交点9. 如图所示,已知∠1=∠2,若添加一个条件使△ABC≌△ADC, 则添加错误的是( )
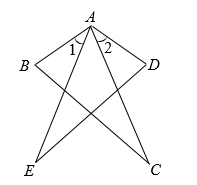
7. 等腰三角形的两边长分别是 和 ,则它的周长是( )A、 B、 C、 或 D、以上都不对8. 到三角形的三边距离相等的点是( )A、三角形三条高的交点 B、三角形三个内角平分线的交点 C、三角形三条中线的交点 D、三角形三边的垂直平分线的交点9. 如图所示,已知∠1=∠2,若添加一个条件使△ABC≌△ADC, 则添加错误的是( )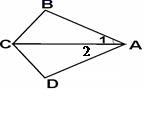 A、AB=AD B、∠B=∠D C、∠BCA=∠DCA D、BC=DC10. 如图, 平分 , 于点A,点Q是射线 上一个动点,若 ,则 的最小值为( )
A、AB=AD B、∠B=∠D C、∠BCA=∠DCA D、BC=DC10. 如图, 平分 , 于点A,点Q是射线 上一个动点,若 ,则 的最小值为( )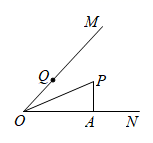 A、1 B、2 C、3 D、411. 如图所示,点 为 内一点,分别作出 点关于 的对称点 ,连接 交 于 ,交 于 ,则 的周长为( )
A、1 B、2 C、3 D、411. 如图所示,点 为 内一点,分别作出 点关于 的对称点 ,连接 交 于 ,交 于 ,则 的周长为( )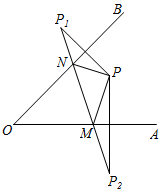 A、 B、 C、 D、12. 如图,在平面直角坐标系中,O是坐标原点,已知点A的坐标为(1 , 1),请你在坐标轴上找出点B,使△AOB为等腰三角形,满足条件的点B的个数为( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中,O是坐标原点,已知点A的坐标为(1 , 1),请你在坐标轴上找出点B,使△AOB为等腰三角形,满足条件的点B的个数为( )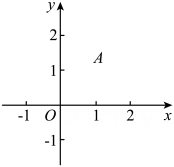 A、6 B、7 C、8 D、9
A、6 B、7 C、8 D、9二、填空题
-
13. 在 中, , ,则 的形状是三角形.14. 一个正多边形内角和等于540°,则这个正多边形的每一外角等于°.15. 如图,点B在AE上,∠CAB=∠DAB , 要使 ,可补充的一个条件是: .
 16. 中,∠C=90°,∠A=30°,若BC=3,则AB=.17. 如图,长方形 沿 折叠,使点 落在 边上的点 处,如果 ,则 度.
16. 中,∠C=90°,∠A=30°,若BC=3,则AB=.17. 如图,长方形 沿 折叠,使点 落在 边上的点 处,如果 ,则 度.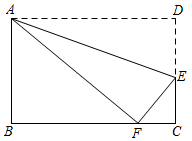 18. 如图,点 在 的边上, , ,则 度.
18. 如图,点 在 的边上, , ,则 度.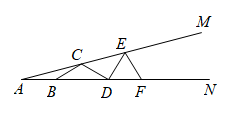
三、解答题
-
19. 如图,在平面直角坐标系中, 的三个顶点的坐标为 ,
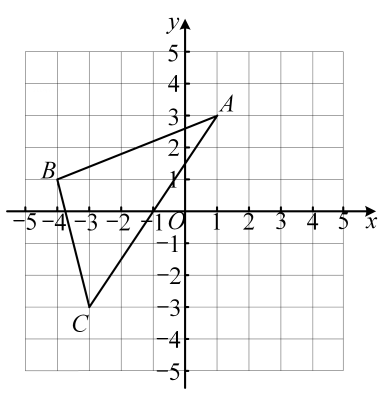 (1)、在图中画出 关于 轴对称的 ;(2)、写出 的坐标; , , .(3)、请在 轴上找到一点 ,使 到 两点的距离之和最小(不写作法,保留痕迹,不用证明).20. 如图,已知 和A、B两点.求作点P,使P到A、B两点的距离相等,且P到 两边距离也相等(不写作法,保留作图痕迹, 写出结论).
(1)、在图中画出 关于 轴对称的 ;(2)、写出 的坐标; , , .(3)、请在 轴上找到一点 ,使 到 两点的距离之和最小(不写作法,保留痕迹,不用证明).20. 如图,已知 和A、B两点.求作点P,使P到A、B两点的距离相等,且P到 两边距离也相等(不写作法,保留作图痕迹, 写出结论).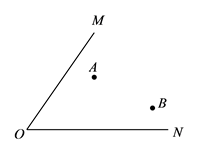 21. 已知如图,AB∥CD,∠A=45°,∠C=∠E.求∠C的度数.
21. 已知如图,AB∥CD,∠A=45°,∠C=∠E.求∠C的度数.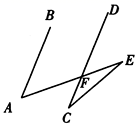 22. 如图,△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,求△ABC的周长.
22. 如图,△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,求△ABC的周长.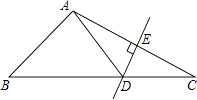 23. 如图,已知 .请将下列说明 的理由补充完整.
23. 如图,已知 .请将下列说明 的理由补充完整.
证明: (已知)
∴ ▲ (两直线平行,内错角相等)
又 (已知)
∴ ▲ (等式的性质)
在 和 中
( ▲ )
(全等三角形的对应边相等).