广西壮族自治区崇左市江州区2021-2022学年八年级上学期数学期中考试试卷
试卷更新日期:2021-11-26 类型:期中考试
一、单选题
-
1. 在平面直角坐标系中,点P(1,-4)位于( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列函数中,属于正比例函数的是( ).A、 B、y=−x+1 C、 D、3. 下列长度的三条线段能组成三角形的是( ).A、3cm,4cm,8cm B、5cm,6cm,11cm C、2cm,2cm,1cm D、4cm,6cm,12cm4. 将点P (−1,-5)平移得到点P′(-4,-5),则它平移的方式是( ).A、向左平移3个单位长度 B、向右移3个单位长度 C、向上移3个单位长度 D、向下移3个单位长度5. 已知直线y= -3x-4与直线y=kx+2平行,则k的值为( ).A、-3 B、3 C、-4 D、46. 已知点C(-1,-2),D(-1,2),则线段CD的长是( ).A、1 B、2 C、3 D、47. 已知点(-4, ),(2, )都在直线 上,则 的大小关系是( ).A、 B、 C、 D、不能比较8. 如图所示,为估计池塘两岸A , B间的距离,一位同学在池塘一侧选取了一点P , 测得PA=16m , PB=12m , 那么A , B间的距离不可能是( )
 A、15m B、18m C、26m D、30m9. 已知△ABC中,∠A=40°,∠B=∠C,那么△ABC是( ).A、直角三角形 B、锐角三角形 C、等边三角形 D、钝角三角形10. 若点P到两坐标轴的距离相等,且ab=4,则点P的坐标为( ).A、(2,2) B、(−2,−2) C、(2,2)或(−2,−2) D、(2,2)或(2,−2)11. 已知 , 是等腰三角形的两边长,且a,b满足 ,则此等腰三角形的周长为( ).A、8 B、6或8 C、7 D、7或812. 如图,直线 与 相交于点P,点P的横坐标为-1,则关于x的不等式 的解集在数轴上表示正确的是( )
A、15m B、18m C、26m D、30m9. 已知△ABC中,∠A=40°,∠B=∠C,那么△ABC是( ).A、直角三角形 B、锐角三角形 C、等边三角形 D、钝角三角形10. 若点P到两坐标轴的距离相等,且ab=4,则点P的坐标为( ).A、(2,2) B、(−2,−2) C、(2,2)或(−2,−2) D、(2,2)或(2,−2)11. 已知 , 是等腰三角形的两边长,且a,b满足 ,则此等腰三角形的周长为( ).A、8 B、6或8 C、7 D、7或812. 如图,直线 与 相交于点P,点P的横坐标为-1,则关于x的不等式 的解集在数轴上表示正确的是( )
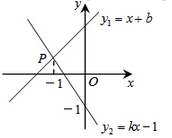 A、
A、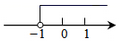 B、
B、 C、
C、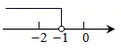 D、
D、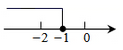
二、填空题
-
13. 函数y= 中,自变量x的取值范围是 .14. 已知一次函数y=(m+2)x-5,若y随x的增大而减小,则m的取值范围为.15. 若直线 经过(2,−1),则b=.16. 一个等腰三角形的两边长分别为 和 ,则它的周长为 .17. 直线 经过第一、二、三象限,则m=.18. 弹簧的长度ycm与所挂物体的质量x(kg)的关系是一次函数,图象如图所示,则弹簧不挂物体时的长度是.

三、解答题
-
19. 若y与x−1成正比例,且x=2,y=3,(1)、求y与x之间的函数关系式;(2)、当x=−2时,y的值是多少?20. 如图,已知△ABC.
 (1)、若AB=3,AC=4,求BC的取值范围;(2)、点D为BC延长线上一点,过点D作DE∥AC,交BA的延长线于点E,若∠E=60°,∠ACD=125°,求∠B的度数.21. 在平面直角坐标系中,△ABC的三个顶点的位置如图所示,将△ABC向左平移3个单位,再向下平移2个单位.
(1)、若AB=3,AC=4,求BC的取值范围;(2)、点D为BC延长线上一点,过点D作DE∥AC,交BA的延长线于点E,若∠E=60°,∠ACD=125°,求∠B的度数.21. 在平面直角坐标系中,△ABC的三个顶点的位置如图所示,将△ABC向左平移3个单位,再向下平移2个单位. (1)、写出△ABC的三个顶点坐标;(2)、请画出平移后的△A′B′C′,并求出△A′B′C′的面积.22. 如图,AD为△ABC的中线,BE为△ABD的中线.
(1)、写出△ABC的三个顶点坐标;(2)、请画出平移后的△A′B′C′,并求出△A′B′C′的面积.22. 如图,AD为△ABC的中线,BE为△ABD的中线. (1)、在△BED中作BD边上的高,垂足为F;(2)、若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?23. 如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD与CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.
(1)、在△BED中作BD边上的高,垂足为F;(2)、若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?23. 如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD与CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.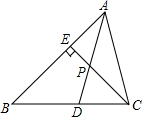 24. 为了保护学生的视力,课桌的高度 与椅子的高度 (不含靠背)都是按 是 的一次函数关系配套设计的,下表列出了两套符合条件课桌椅的高度:
24. 为了保护学生的视力,课桌的高度 与椅子的高度 (不含靠背)都是按 是 的一次函数关系配套设计的,下表列出了两套符合条件课桌椅的高度:第一套
第二套
椅子高度
40.0
37.0
课桌高度
75.0
70.2
(1)、请求出 与 的函数关系式(不要求写出 的取值范围);(2)、现有一把高 的椅子和一张高 的课桌,它们是否配套?请通过计算说明理由.25. 直线 y=2x-2与x轴交于点D,直线 y=kx+b与x轴交于点A,且经过B(3,1),两直线相交于点C(m,2). (1)、求直线 的解析式和点C的坐标.(2)、求当x取何值,kx+b≥2x-2(3)、△ADC的面积.26. 某超市预购进A、B两种品牌的T恤共200件,已知两种T恤的进价如表所示,设购进A种T恤x件,且所购进的两种T恤全部卖出,获得的总利润为W元.
(1)、求直线 的解析式和点C的坐标.(2)、求当x取何值,kx+b≥2x-2(3)、△ADC的面积.26. 某超市预购进A、B两种品牌的T恤共200件,已知两种T恤的进价如表所示,设购进A种T恤x件,且所购进的两种T恤全部卖出,获得的总利润为W元.品牌
进价/(元/件)
售价/(元/件)
A
50
80
B
40
65
(1)、求W关于x的函数关系式;(2)、如果购进两种T恤的总费用不超过9500元,那么超市如何进货才能获得最大利润?并求出最大利润.(提示:利润=售价﹣进价)