人教版中考数学重难点突破专题练习：一元二次方程【湖南】

试卷更新日期：2021-11-26 类型：一轮复习

进入出卷网下载

一、计算题

1.

(1)、用直接开平方法解下列方程：9x²﹣81＝0；

(2)、用配方法解一元二次方程：x²﹣6x﹣9＝0.

查看试题解析
2. 解方程

(1)、 $x^{2} - 7 x + 10 = 0$ ；

(2)、 ${(x + 4)}^{2} = 5 (x + 4)$ .

查看试题解析
3. 解一元二次方程：

(1)、 $x^{2} + 2 x - 2 = 0$

(2)、 $2 x^{2} - 5 x - 3 = 0$

查看试题解析
4. 解方程：

(1)、 $x^{2} + 2 x - 3 = 0$

(2)、 $3 x (x - 1) = 2 (1 - x)$ .

查看试题解析
5. 先化简，再求值：
$(a + b) (a - b) + {(a - b)}^{2} - (2 a^{2} - a b)$ ，其中a，b是一元二次方程 $x^{2} + x - 2 = 0$ 的两个实数根.

查看试题解析

二、综合题

6. 已知：关于 $x$ 的一元二次方程 $x^{2} - 3 x - k = 0$ 有两个不相等的实数根.

(1)、求 $k$ 的取值范围；

(2)、请选择一个 $k$ 的负整数值，并求出方程的根.

查看试题解析
7. 若x₁ ， x₂是关于x的一元二次方程ax²+bx+c＝0的两个根，则x₁+x₂＝﹣ $\frac{b}{a}$ ，x₁•x₂＝ $\frac{c}{a}$ .现已知一元二次方程px²+2x+q＝0的两根分别为m，n.

(1)、若m＝2，n＝﹣4，求p，q的值；

(2)、若p＝3，q＝﹣1，求m+mn+n的值.

查看试题解析
8. 某地区2019年投入教育经费2000万元，2021年投入教育经费2880万元.

(1)、求2019年至2021年该地区投入教育经费的年平均增长率；

(2)、根据（1）所得的年平均增长率，预计2022年该地区将投入教育经费多少万元.

查看试题解析
9. 定义；若关于x的一元二次方程ax²+bx+c＝0有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，若函数G₁的图象与函数G₂的图象相交于A、B两点，其中一个点的横坐标等于另一点的横坐标的2倍，则称函数G₁与函数G₂互为“倍根函数”，A、B两点间的水平距离为“倍宽”.

(1)、若 $(x - 4) (2 x + k) = 0$ 是“倍根方程”，求k的值；

(2)、函数 $y = - m x$ 与 $y = x^{2} - k$ 互为“倍根函数”且“倍宽”为2，求 $m ， k$ 的值；

(3)、直线l：y＝tx+d与抛物线L：y＝2x²+px+q（q≠d）互为“倍根函数”，若直线l与抛物线L相交于A（x₁ ， y₁），B（x₂ ， y₂）两点，且2+2t²≤AB²≤3+3t² ，令6x₀＝|p﹣t|，若二次函数y₀＝﹣（x₀﹣m）²+m²+1有最大值4，求实数m的值.

查看试题解析
10. 利用完全平方公式进行因式分解，解答下列问题：

(1)、因式分解：x²﹣4x+4＝.

(2)、填空：
①当x＝﹣2时，代数式x²+4x+4＝.

②当x＝时，代数式x²﹣6x+9＝0.

③代数式x²+8x+20的最小值是.

(3)、拓展与应用：求代数式a²+b²﹣6a+8b+28的最小值.

查看试题解析
11. 如果关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 有两个实数根，且其中一个根为另一个根的 $k ((k > 0)$ 倍，则称这样的方程为“k系方程”.如方程 $(x - 1) (x - 2) = 0$ 的两根分别为： $x_{1} = 1 ， x_{2} = 2 ， x_{2} = 2 x_{1}$ ，则方程 $(x - 1) (x - 2) = 0$ 为“2系方程”.

(1)、下列方程是“3系方程”的是（填序号即可）；
① $(3 x + 1) (x + 1) = 0$ ；② $x^{2} - 2 x - 3 = 0$ ；③ ${(x - 4)}^{2} = 4$ .

(2)、若关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 是“2系方程”.
①求证： $b^{2} - \frac{9}{2} a c = 0$ ；

②若 $c = 2$ ，且关于x的函数 $y = a x^{2} - \frac{b^{2}}{3} x + 2$ ，当 $\frac{1}{a} \leq x \leq \frac{2 a + 1}{a}$ 时的最大值为1，求a的值.

查看试题解析
12. 机械加工需要用油进行润滑以减小摩擦，某企业加工一台大型机械设备润滑用油量为90千克，用油的重复利用率为60%，按此计算，加工一台大型机械设备的实际耗油量为36千克，为了建设节约型社会，减少油耗，该企业的甲、乙两个车间都组织了人员为减少实际耗油量进行攻关.

(1)、甲车间通过技术革新后，加工一台大型机械设备润滑用油量下降到70千克，用油量的重复利用率仍然为60%.问甲车间技术革新后，加工一台大型机械设备的实际耗油量是多少千克？

(2)、乙车间通过技术革新后，不仅降低了润滑用油量，同时也提高了用油的重复利用率，并且发现在技术革新前的基础上，润滑用油量每减少1千克，用油的重复利用率将增加1.6%，这样乙车间加工一台大型机械设备的实际耗油量下降到12千克，问乙车间技术革新后，加工一台大型机械设备的润滑用油量是多少千克？用油的重复利用率是多少？

查看试题解析
13. 随着某市养老机构建设的稳步推进，拥有的养老床位不断增加.

(1)、该市的养老床位数从2018年底的2万个增长到2020年底的2.88万个，求该市这两年（从2018年度到2020年底）拥有的养老床位数的平均年增长率；

(2)、若该市某社区今年准备新建一养老中心，其中规划建造三类养老专用房间共100间，这三类养老专用房间分别为单人间t个（1个养老床位），双人间（2个养老床位），三人间（3个养老床位），因实际需要（ $10 \leq t \leq 30$ ），且双人间的房间数是单人间的2倍.设该养老中心建成后能提供养老床位y个，求y与t的函数关系式

查看试题解析
14. 已知：关于x的一元二次方程 ${kx}^{2} - (4k + 1) x + 3k + 3 = 0$ （k是整数）.

(1)、求证：方程有两个不相等的实数根；

(2)、若方程的两个实数根分别为x₁ ， x₂（其中x₁＜x₂），设 $y = x_{2} - x_{1} - 2$ ，判断y是否为变量k的函数？如果是，请写出函数解析式；若不是，请说明理由.

查看试题解析
15. 已知关于 $x$ 的一元二次方程 $x^{2} - 4 x + m + 1 = 0$ 有实数根.

(1)、若1是方程的一个根，求出一元二次方程的另一根；

(2)、若方程的两个实数根为 $x_{1}$ ， $x_{2}$ ，且 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ =3，求 $m$ 的值.

查看试题解析
16. 列方程解应用题
如图是一个窗户的框架图，下面部分窗户的高是上面窗户部分的高的二倍，窗户的宽比窗户下面部分的高要多0.4m.

(1)、若窗户的面积是4.8m² ，请求出窗户的宽和高；

(2)、若一根铝合金料的长是4m，要做成上面的窗户需要准备几根这样的铝合金料？若是6m长的话又用几根？

查看试题解析
17. 某商场销售一批名牌衬衫，平均每天能售出20件，每件盈利40元。经调查发现：如果这种衬衫的售价每降低1元时，平均每天能多售出2件.设每件衬衫降价x元.

(1)、降价后，每件衬衫的利润为元，销量为件；（用含x的式子表示）

(2)、为了扩大销售，尽快减少库存，商场决定釆取降价措施。但需要平均每天盈利1200元，求每件衬衫应降价多少元？

查看试题解析
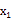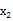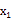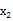18. 已知方程 +px+q＝0的两个根是，，那么 + ＝－p， $x_{1}$ $x_{2}$ ＝q，反过来，如果 $x_{1}$ + $x_{2}$ ＝－p， $x_{1}$ $x_{2}$ ＝q，那么以 $x_{1}$ ， $x_{2}$ 为两根的一元二次方程是 $x^{2}$ +px+q＝0．请根据以上结论，解决下列问题：

(1)、已知关于x的方程 $x^{2}$ +mx+n＝0(n≠0)，求出—个一元二次方程，使它的两根分别是已知方程两根的倒数．

(2)、已知a、b满足 $a^{2}$ －15a－5＝0， $b^{2}$ －15b－5＝0，求 $\frac{a}{b} + \frac{b}{a}$ 的值．

(3)、已知a、b、c均为实数，且a+b+c＝0，abc＝16，求正数c的最小值

查看试题解析
19. 我们不妨约定：若某函数图象上至少存在不同的两点关于原点对称，则把该函数称之为“H函数”，其图像上关于原点对称的两点叫做一对“H点”，根据该约定，完成下列各题

(1)、在下列关于x的函数中，是“H函数”的，请在相应题目后面的括号中打“√”，不是“H函数”的打“×”
① $y = 2 x$ （）

② $y = \frac{m}{x} (m \neq 0)$ （）

③ $y = 3 x - 1$ （）

(2)、若点 $A (1 ， m)$ 与点 $B (n ， - 4)$ 关于x的“H函数” $y = a x^{2} + b x + c (a \neq 0)$ 的一对“H点”，且该函数的对称轴始终位于直线 $x = 2$ 的右侧，求 $a ， b ， c$ 的值域或取值范围；

(3)、若关于x的“H函数” $y = a x^{2} + 2 b x + 3 c$ （a，b，c是常数）同时满足下列两个条件：① $a + b + c = 0$ ，② $(2 c + b - a) (2 c + b + 3 a) < 0$ ，求该H函数截x轴得到的线段长度的取值范围．

查看试题解析
20. 关于 $x$ 的一元二次方程 $x^{2} - 3 x + k = 0$ 有实数根．

(1)、求 $k$ 的取值范围；

(2)、如果 $k$ 是符合条件的最大整数，且一元二次方程 $(m - 1) x^{2} + x + m - 3 = 0$ 与方程 $x^{2} - 3 x + k = 0$ 有一个相同的根，求此时 $m$ 的值．

查看试题解析