陕西省宝鸡市陈仓区2021-2022学年九年级上学期数学期中考试试卷

试卷更新日期：2021-11-26 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程是一元二次方程的是（）

A、2x﹣3y+1 B、3x+y＝z C、x²﹣5x＝1 D、x²﹣ $\frac{1}{x}$ +2＝0

查看试题解析
2. 如图，将矩形ABCD沿对角线BD折叠，使点C落在F处，BF交AD于点E．若∠BDC＝62°，则∠DEF的度数为（）

A、31° B、28° C、62° D、56°

查看试题解析
3. 若方程 $x^{2} - 2 x + m = 0$ 没有实数根，则 $m$ 的值可以是（）

A、-1 B、0 C、0 D、 $\sqrt{3}$

查看试题解析
4. 如图，顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，则应添加的条件是（）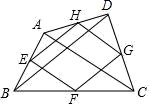

A、AB//CD B、AC⊥BD C、AC=BD D、AD=BC

查看试题解析
5. 某班学生做“用频率估计概率”的实验时，给出的某一结果出现如图所示的统计图，则符合这一结果的实验可能是（　　）

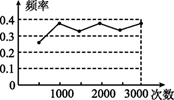A、抛一枚硬币，出现正面朝上 B、从标有1，2，3，4，5，6的六张卡片中任抽一张，出现偶数 C、从一个装有6个红球和3个黑球的袋子中任取一球，取到的是黑球 D、先后两次掷一枚质地均匀的正六面体骰子，两次向上的点数之和是7

查看试题解析
6. 如图，在菱形ABCD中，对角线AC，BD相交于点O，BD＝6，AC＝8，直线OE⊥AB交CD于点F，则EF的长为（）

A、4.8 B、 $2 \sqrt{7}$ C、5 D、6

查看试题解析
7. 已知 $x = 1$ 是一元二次方程 $(m - 2) x^{2} + 4 x - m^{2} = 0$ 的一个根，则m的值为（）

A、-1或2 B、-1 C、2 D、0

查看试题解析
8. 如图，在矩形ABCD中，AB＝5，AD＝3，点E为BC上一点，把△CDE沿DE翻折，点C 恰好落在AB边上的F处，则CE的长是（）

A、1 B、 $\frac{4}{3}$ C、 $\frac{3}{2}$ D、 $\frac{5}{3}$

查看试题解析

二、填空题

9. 中国古代数学家杨辉的《田亩比数乘除减法》中记载：“直田积八百六十四步，只云阔不及长一十二步，问阔及长各几步？翻译成数学问题是：一块矩形田地的面积为864平方步，它的宽比长少12步，问它的长与宽各多少步？利用方程思想，设宽为x步，则依题意列方程为．

查看试题解析
10. 已知关于 $x$ 的一元二次方程 $m x^{2} - x + 2 = 0$ 有两个不相等的实数根，则实数 $m$ 的取值范围是.

查看试题解析
11. 如图， $A D ∥ B C$ ， $A B ∥ D C$ ， $A B = 4$ ， $∠ A D E = 150 °$ ，那么 $∠ A =$ 时，四边形 $A B C D$ 是菱形.

查看试题解析
12. 若m是方程 $2 x^{2} - 3 x - 1 = 0$ 的一个根，则 $6 m^{2} - 9 m + 2020$ 的值为.

查看试题解析
13. 如图，在边长为 $4$ 的正方形 $A B C D$ 中，点 $E$ 、 $F$ 分别是边 $B C$ 、 $C D$ 上的动点.且 $B E = C F$ ，连接 $B F$ 、 $D E$ ，则 $B F + D E$ 的最小值为.

查看试题解析

三、解答题

14. 用配方法解方程 $2 x^{2} + 5 x = 12$ ．

查看试题解析
15. 公式法解一元二次方程：2x²﹣4x﹣1＝0.

查看试题解析

16. 小敏与小霞两位同学解方程

3 (x - 3) = {(x - 3)}^{2}

的过程如下框：

小敏：

两边同除以 $(x - 3)$ ，得

$3 = x - 3$ ，

则 $x = 6$ ．

小霞：

移项，得 $3 (x - 3) - {(x - 3)}^{2} = 0$ ，

提取公因式，得 $(x - 3) (3 - x - 3) = 0$ ．

则 $x - 3 = 0$ 或 $3 - x - 3 = 0$ ，

解得 $x_{1} = 3$ ， $x_{2} = 0$ ．

你认为他们的解法是否正确？若正确请在框内打“√”；若错误请在框内打“×”，并写出你的解答过程．

查看试题解析

17. 如图，四边形ABCD为正方形，连接AC，请用尺规作图法在边BC上求作一点P，使得点P到AC的距离等于BP的长度.（保留作图痕迹，不写作法）

查看试题解析

18. 王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀，让若干学生进行摸球试验，每次摸出一个球（有放回），表格是活动进行中的一组统计数据：

摸球的次数 $n$	100	150	200	500	800	1000
摸到黑球的次数 $m$	23	31	60	130	203	251
摸到黑球的频率 $\frac{m}{n}$	0.23	0.21	0.30	0.26	0.235	0.251

(1)、根据上表数据估计从袋中摸出一个球是黑球的概率是；（精确到

0.01

）

(2)、估算袋中白球的个数.

查看试题解析

19. “杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水箱亩产量700公斤的目标，第三阶段实现水稻亩产量1008公斤的目标．

(1)、如果第二阶段、第三阶段亩产量的增长率相同，求亩产量的平均增长率；

(2)、按照（1）中亩产量增长率，科研团队期望第四阶段水稻亩产量达到1200公斤，请通过计算说明他们的目标能否实现．

查看试题解析
20.
已知：如图，在矩形ABCD中，点E在边AB上，点F在边BC上，且BE=CF，EF⊥DF，求证：BF=CD．

查看试题解析
21. 为庆祝建党100周年，某大学组织志愿者周末到社区进行党史学习宣讲，决定从A ， B ， C ， D四名志愿者中通过抽签的方式确定两名志愿者参加．抽签规则：将四名志愿者的名字分别写在四张完全相同不透明卡片的正面，把四张卡片背面朝上，洗匀后放在桌面上，先从中随机抽取一张卡片，记下名字，再从剩余的三张卡片中随机抽取第二张，记下名字，

(1)、“A志愿者被选中”是事件（填“随机”或“不可能”或“必然”）；

(2)、请你用列表法或画树状图法表示出这次抽签所有可能的结果，并求出A ， B两名志愿者被选中的概率．

查看试题解析
22. 如图，将▱ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F．

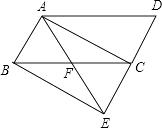(1)、求证：△ABF≌△ECF；

(2)、若∠AFC=2∠D，连接AC、BE，求证：四边形ABEC是矩形．

查看试题解析
23. 关于x的一元二次方程x²﹣3x＋k＝0有实数根.

(1)、求k的取值范围；

(2)、若k是符合条件的最大整数，求此时一元二次方程的解.

查看试题解析
24. 如图，矩形 $A B C D$ 中， $A B = 8$ ， $A D = 6$ ，点 $O$ 是对角线 $B D$ 的中点，过点 $O$ 的直线分别交 $A B$ 、 $C D$ 边于点 $E$ 、 $F$ .

(1)、求证：四边形 $D E B F$ 是平行四边形；

(2)、当 $D E = D F$ 时，求四边形 $D E B F$ 的面积.

查看试题解析
25. 列方程（组）解应用题
端午节期间，某水果超市调查某种水果的销售情况，下面是调查员的对话：

小王：该水果的进价是每千克22元；

小李：当销售价为每千克38元时，每天可售出160千克；若每千克降低3元，每天的销售量将增加120千克．

根据他们的对话，解决下面所给问题：超市每天要获得销售利润3640元，又要尽可能让顾客得到实惠，求这种水果的销售价为每千克多少元？

查看试题解析
26. 如图1，对角线互相垂直的四边形叫做垂美四边形.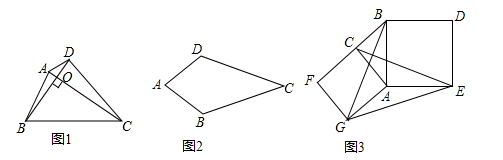

(1)、概念理解：如图2，在四边形 $A B C D$ 中， $A B = A D$ ， $C B = C D$ ，问四边形 $A B C D$ 是垂美四边形吗？请说明理由；

(2)、性质探究：如图1，四边形 $A B C D$ 的对角线 $A C$ 、 $B D$ 交于点 $O$ ， $A C ⊥ B D$ .试证明： $A B^{2} + C D^{2} = A D^{2} + B C^{2}$ ；

(3)、解决问题：如图3，分别以 $R t △ A C B$ 的直角边 $A C$ 和斜边 $A B$ 为边向外作正方形 $A C F G$ 和正方形 $A B D E$ ，连结 $C E$ 、 $B G$ 、 $G E$ .已知 $A C = 4$ ， $A B = 5$ ，求 $G E$ 的长.

查看试题解析