广西壮族自治区河池市凤山县2021-2022学年九年级上学期数学期中考试试卷
试卷更新日期:2021-11-26 类型:期中考试
一、单选题
-
1. 下列四个图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、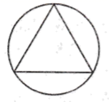 C、
C、 D、
D、 2. 一元二次方程 的二次项系数、一次项系数分别是A、3, B、3,1 C、 ,1 D、3,63. 如图,把△AOB绕点O顺时针旋转得到△COD,则旋转角是( )
2. 一元二次方程 的二次项系数、一次项系数分别是A、3, B、3,1 C、 ,1 D、3,63. 如图,把△AOB绕点O顺时针旋转得到△COD,则旋转角是( ) A、∠AOC B、∠AOD C、∠AOB D、∠BOC4. 将抛物线y=2x2平移后得到抛物线y=2x2+1,则平移方式为( )A、向左平移1个单位 B、向右平移1个单位 C、向上平移1个单位 D、向下平移1个单位5. 若关于x的一元二次方程的两个根为x1=1,x2=2,则这个方程可能是( )A、x2-3x+2=0 B、x2+3x+2=0 C、x2+3x-2=0 D、x2-2x+3=06. 如图,若要使 与 平行,则 绕点 至少旋转的度数是( )
A、∠AOC B、∠AOD C、∠AOB D、∠BOC4. 将抛物线y=2x2平移后得到抛物线y=2x2+1,则平移方式为( )A、向左平移1个单位 B、向右平移1个单位 C、向上平移1个单位 D、向下平移1个单位5. 若关于x的一元二次方程的两个根为x1=1,x2=2,则这个方程可能是( )A、x2-3x+2=0 B、x2+3x+2=0 C、x2+3x-2=0 D、x2-2x+3=06. 如图,若要使 与 平行,则 绕点 至少旋转的度数是( )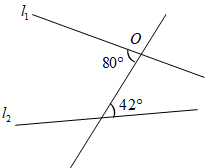 A、 B、 C、 D、7. 抛物线 , , 共有的性质是( )A、开口向上 B、对称轴是 轴 C、都有最高点 D、 随 值的增大而增大8. 若二次函数y=x2+mx的图象的对称轴是直线x=3,则关于x的方程x2+mx=7的解为( )A、x1=0,x2=6 B、x1=1,x2=7 C、x1=1,x2=-7 D、x1=-1,x2=79. 某商店今年1月份的销售额是2万元,3月份的销售额是4.5万元,从1月份到3月份,该店销售额平均每月的增长率是( )A、20% B、25% C、50% D、62.5%10. 如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )
A、 B、 C、 D、7. 抛物线 , , 共有的性质是( )A、开口向上 B、对称轴是 轴 C、都有最高点 D、 随 值的增大而增大8. 若二次函数y=x2+mx的图象的对称轴是直线x=3,则关于x的方程x2+mx=7的解为( )A、x1=0,x2=6 B、x1=1,x2=7 C、x1=1,x2=-7 D、x1=-1,x2=79. 某商店今年1月份的销售额是2万元,3月份的销售额是4.5万元,从1月份到3月份,该店销售额平均每月的增长率是( )A、20% B、25% C、50% D、62.5%10. 如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )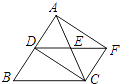 A、矩形 B、菱形 C、正方形 D、梯形11. 当ab>0时,y=ax2与y=ax+b的图象大致是( )A、
A、矩形 B、菱形 C、正方形 D、梯形11. 当ab>0时,y=ax2与y=ax+b的图象大致是( )A、 B、
B、 C、
C、 D、
D、 12. 如图,是抛物线 图象的一部分,抛物线的顶点坐标为 ,与 轴的一个交点为 .直线 经过点 和点 .以下结论:
12. 如图,是抛物线 图象的一部分,抛物线的顶点坐标为 ,与 轴的一个交点为 .直线 经过点 和点 .以下结论:① ;② ;③抛物线与 轴的另一个交点是 ;④方程 有两个不相等的实数根;⑤ ;⑥不等式 的解集为 .其中结论正确的是( )
 A、①④⑥ B、②⑤⑥ C、②③⑤ D、①⑤⑥
A、①④⑥ B、②⑤⑥ C、②③⑤ D、①⑤⑥二、填空题
-
13. 若点M(3,a﹣2),N(b,a)关于原点对称,则a+b= .14. 如果一元二次方程 的两根分别为 , ,那么 .15. 如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=3,则BE=.
 16. 关于x的一元二次方程 (a-1)x2+(2a+1)x+a=0 有两个不相等的实数根,则a的取值范围是.17. 若将图中的抛物线y=x2-2x+c向上平移,使它经过点(2,0),则此时的抛物线位于x轴下方的图象对应x的取值范围是.
16. 关于x的一元二次方程 (a-1)x2+(2a+1)x+a=0 有两个不相等的实数根,则a的取值范围是.17. 若将图中的抛物线y=x2-2x+c向上平移,使它经过点(2,0),则此时的抛物线位于x轴下方的图象对应x的取值范围是.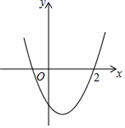 18. 如图,正方形 的点 在 轴的负半轴上,点 在 轴的负半轴上,抛物线 的顶点为 ,且经过点 、 .若 为等腰直角三角形,则 的值是.
18. 如图,正方形 的点 在 轴的负半轴上,点 在 轴的负半轴上,抛物线 的顶点为 ,且经过点 、 .若 为等腰直角三角形,则 的值是.
三、解答题
-
19. 用适当的方法解下列方程:(1)、 ;(2)、 .20. 如图, 的顶点坐标分别为 , .

⑴画出 关于点 的中心对称图形 ;
⑵画出 绕原点 逆时针旋转 的 ,直接写出点 的坐标
⑶若 内一点 绕原点 逆时针旋转 的上对应点为 ,请写出 的坐标.(用含 , 的式子表示).
21. 若关于x的二次方程(m+1)x2+5x+m2﹣3m=4的常数项为0,求m的值.22. 已知抛物线y=x2﹣(2m﹣1)x+m2﹣m.(1)、求证:此抛物线与x轴必有两个不同的交点;(2)、若此抛物线与直线y=x﹣3m+3的一个交点在y轴上,求m的值.23. 已知抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),B(3,0).(1)、求抛物线的解析式;(2)、过点D(0, )作x轴的平行线交抛物线于E,F两点,求EF的长;(3)、当y≤ 时,直接写出x的取值范围是.24. 如图是一张长10 dm,宽6 dm矩形纸板,将纸板四个角各剪去一个同样的边长为x dm的正方形,然后将四周突出部分折起,可制成一个无盖方盒.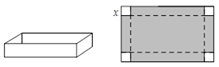 (1)、无盖方盒盒底的长为dm,宽为dm(用含x的式子表示)(2)、若要制作一个底面积是32dm2的一个无盖长方体纸盒,求剪去的正方形边长x.25. 如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)、无盖方盒盒底的长为dm,宽为dm(用含x的式子表示)(2)、若要制作一个底面积是32dm2的一个无盖长方体纸盒,求剪去的正方形边长x.25. 如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证: (1)、EA是∠QED的平分线;(2)、EF2=BE2+DF2 .26. 如图①,直线 分别交 轴和 轴于点 和点 ,将 绕点 逆时针旋转 得到 .抛物线 经过 、 、 三点.
(1)、EA是∠QED的平分线;(2)、EF2=BE2+DF2 .26. 如图①,直线 分别交 轴和 轴于点 和点 ,将 绕点 逆时针旋转 得到 .抛物线 经过 、 、 三点. (1)、求抛物线 的表达式;(2)、若与 轴平行的直线 以 秒钟一个单位长的速度从 轴向左平移,交线段 于点 、交抛物线 于点 ,求线段 的最大值;(3)、如图②,点 为抛物线 的顶点,点 是抛物线 在第二象限的上一动点(不与点 、 重合),连接 ,以 为边作图示一侧的正方形 .随着点 的运动,正方形的大小、位置也随之改变,当顶点 恰好落在 轴的负半轴时,试求出此时点 的坐标.
(1)、求抛物线 的表达式;(2)、若与 轴平行的直线 以 秒钟一个单位长的速度从 轴向左平移,交线段 于点 、交抛物线 于点 ,求线段 的最大值;(3)、如图②,点 为抛物线 的顶点,点 是抛物线 在第二象限的上一动点(不与点 、 重合),连接 ,以 为边作图示一侧的正方形 .随着点 的运动,正方形的大小、位置也随之改变,当顶点 恰好落在 轴的负半轴时,试求出此时点 的坐标.