广西壮族自治区崇左市江州区2021-2022学年九年级上学期数学期中考试试卷

试卷更新日期：2021-11-26 类型：期中考试

进入出卷网下载

一、单选题

1. 在下列函数中表示y关于x 的反比例函数的是（）

A、y=2x B、 $y = \frac{2}{x}$ C、 $y = \frac{2}{x - 1}$ D、 $y = \frac{2}{x^{2}}$

查看试题解析
2. 下列各组长度的线段（单位： $cm$ ）中，成比例线段的是（）

A、1，2，3，4 B、1，2，3，6 C、2，3，4，5 D、1，3，5，10

查看试题解析
3. 已知3x=5y（y≠0），则下列比例式成立的是（）

A、 $\frac{x}{3} = \frac{5}{y}$ B、 $\frac{x}{5} = \frac{y}{3}$ C、 $\frac{x}{y} = \frac{3}{5}$ D、 $\frac{x}{3} = \frac{y}{5}$

查看试题解析
4. 函数 $y = \frac{k}{x}$ 的图象经过点（－1，－2），则k的值为（）

A、 $\frac{1}{2}$ B、－ $\frac{1}{2}$ C、2 D、－2

查看试题解析
5. 若两个相似三角形的周长之比是1：2，则它们的面积之比是（　　）

A、1：2 B、1： $\sqrt{2}$ C、2：1 D、1：4

查看试题解析
6. 将抛物线y＝2x²向右平移2个单位，再向上平移3个单位所得新抛物线的表达式是（）

A、y＝2（x+2）²+3 B、y＝（x-2）²+3 C、y＝2（x+3）²-2 D、y＝2（x﹣2）²+3

查看试题解析
7. 下列命题中，是真命题的是（）

A、正方形都相似 B、矩形都相似 C、等腰三角形都相似 D、直角三角形都相似

查看试题解析
8. 已知（－2，y₁），（－1，y₂），（1，y₃）都在反比例函数上 $y = \frac{1}{x}$ 的图象上.下列结论正确的是（）

A、y₃>y₁>y₂ B、y₁>y₃>y₂ C、y₁>y₂>y₃ D、y₃>y₂>y₁

查看试题解析
9. 如图，CD是Rt△ABC斜边AB上的高，CD=6，BD=4，则AB的长为（）

A、11 B、12 C、13 D、14

查看试题解析
10. 如图，D，E分别是△ABC的边AB，AC上的点，添加下列条件仍不能判定△ADE与△ABC相似（）

A、DE∥BC B、∠ADE=∠ACB C、 $\frac{A D}{A C} = \frac{A E}{A B}$ D、 $\frac{A D}{A B} = \frac{D E}{B C}$

查看试题解析
11. 如图，点A是反比例函数y＝ $\frac{k}{x}$ 的图象上的一点，过点A作AB⊥x轴，垂足为B.点C为y轴上的一点，连接AC，BC.若△ABC的面积为4，则k的值是（）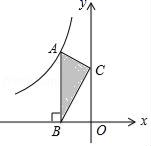

A、4 B、﹣4 C、8 D、﹣8

查看试题解析
12. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，给出下列四个结论：①abc>0；② $b^{2}$ －4ac>0；③a+b+c<0；④2a+b>0；其中结论正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 二次函数y=（x﹣1）²﹣2的顶点坐标是.

查看试题解析
14. 已知抛物线y=(m－1) x²开口向下，则m的取值范围是.

查看试题解析
15. 如图，在 $△ A B C$ 中， $D E / / B C$ ，若 $\frac{A D}{B D} = \frac{1}{2}$ ，则 $\frac{D E}{B C} =$ .

查看试题解析
16. 已知二次函数y＝x²﹣mx+4的顶点在x轴上，则m＝．

查看试题解析
17. 若反比例函数 $y = \frac{k - 2}{x}$ 的图象经过第一、三象限，则 $k$ 的取值范围是．

查看试题解析
18. 如图，一小孩将一只皮球从A处抛出去，它所经过的路线是某个二次函数图象的一部分，如果他的出手处A距地面的距离OA为1 m，当球飞越的水平距离为8米时，球到达最高点B处，离地面高度为9米，则这个二次函数的表达式为.

查看试题解析
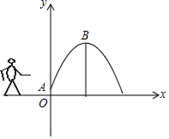19. 如图，D是△ABC的边AC上的一点，连接BD，已知∠ABD=∠C，AB=6，AD=4，求线段CD的长.

查看试题解析

三、解答题

20. 已知二次函数y=ax²＋bx的图象经过点(2，0)和(－1，6).

(1)、求二次函数的解析式；

(2)、求它的对称轴和顶点坐标.

查看试题解析
21. 如图，在边长为1的正方形网格中建立平面直角坐标系，已知△ABC三个顶点分别为A（－1，2），B（2，1），C（4，5）.

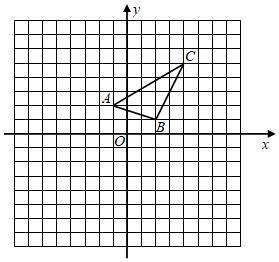
⑴画出△ABC关于x轴对称的△A₁B₁C₁；

⑵以原点O为位似中心，在x轴上方画出△A₂B₂C₂ ，使△A₂B₂C₂与△ABC位似，且相似比为2.

查看试题解析
22. 如图，已知一次函数y＝kx＋b的图象与反比例函数 $y ＝－ \frac{8}{x}$ 的图象交于A、B两点，且点A的横坐标和点B的纵坐标都是－2．

求：

(1)、一次函数的解析式；

(2)、△AOB的面积．

查看试题解析
23. 如图，在4×4的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.

(1)、填空：∠ABC=°，BC=；

(2)、判断△ABC与△DEF是否相似，并证明你的结论.

查看试题解析
24. 如图，在足够大的空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另三边一共用了100米木栏．

(1)、若a=20，所围成的矩形菜园的面积为450平方米，求所利用旧墙AD的长；

(2)、求矩形菜园ABCD面积的最大值．

查看试题解析
25. 如图，在矩形ABCD中，E，F分别是AB，AD的中点，连接AC，EC，EF，FC，且EC⊥EF.

(1)、求证：△AEF∽△BCE；

(2)、若AC= $2 \sqrt{3}$ ，求AB的长.

查看试题解析
26. 如图，已知抛物线 $y = a x^{2} + b x - 2$ 经过A（4，0），B（1，0）.

(1)、求抛物线的解析式；

(2)、P是抛物线上一动点（P不与点A，B，C重合），过点P作PM⊥x轴，垂足为M是否存在点P，使得以A，P，M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标，若不存在，请说明理由.

查看试题解析