广西壮族自治区北海市合浦县2021-2022学年九年级上学期数学期中考试试卷

试卷更新日期：2021-11-26 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程为一元二次方程的是（）

A、 $x^{2} + \frac{1}{x^{2}} = 1$ B、 $x^{2} + x y + 2 = 0$ C、 $a x^{2} + b x + c = 0$ D、 $x^{2} - 3 = 0$

查看试题解析
2. 下列函数中，y是x的反比例函数的是（）.

A、 $y = \frac{2}{x^{2}}$ B、 $y = - \frac{3}{x}$ C、 $y = 2 x$ D、 $\frac{y}{x} = 4$

查看试题解析
3. a，b，c，d是成比例线段，若 $a = 3 cm$ ， $b = 2 cm$ ， $c = 6 cm$ ，则线段d的长为（）

A、4cm B、5cm C、6cm D、7cm

查看试题解析
4. 用配方法解方程 $x^{2} + 4 x - 5 = 0$ 时，原方程应变形为（　　）

A、 ${(x - 2)}^{2} = 1$ B、 ${(x - 4)}^{2} = 11$ C、 ${(x + 2)}^{2} = 9$ D、 ${(x + 4)}^{2} = 21$

查看试题解析
5. 已知函数y＝ $m x$ 的图象在第二、四象限，那么方程mx²﹣3x+2＝0根的情况为（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
6. 下列图形中不一定是相似图形的是（）

A、两个等边三角形 B、两个顶角相等的等腰三角形 C、两个等腰直角三角形 D、两个矩形

查看试题解析
7. 如图，在 $△ A B C$ 中， $D E // B C$ ，若 $A D = 4$ ， $B D = 2$ ，则 $A E ： A C$ 的值为（）

A、 $0.5$ B、2 C、 $\frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
8. 如图， $△ A B C$ 与 $△ D E F$ 是位似图形，点 $O$ 为位似中心，已知 $B O ： O E = 2 ： 1$ ，则 $△ A B C$ 与 $△ D E F$ 的面积比是（）

A、2：1 B、3：1 C、4：1 D、5：1

查看试题解析
9. 如图，将一块正方形空地划出部分区域进行绿化后，原正方形空地一边减少了2m，另一边减少了3m，且剩余一块面积为20m²的矩形空地，设原正方形空地的边长为xm，则可列方程为（）

A、x²﹣5x﹣14＝0 B、x²+5x﹣14＝0 C、x²+5x+14＝0 D、x²﹣5x+14＝0

查看试题解析
10. 在同一直角坐标系中，函数 $y = k x + k$ 与 $y = \frac{- k}{x} (k \neq 0)$ 的图象大致为（）.

A、 B、 C、 D、

查看试题解析
11. 如图，点D、E分别在 $△ A B C$ 的边AB、AC的反向延长线上，下面比例式中，不一定能判断 $E D ∥ B C$ 的是（）

A、 $\frac{B A}{B D} = \frac{C A}{C E}$ B、 $\frac{E A}{A C} = \frac{D A}{A B}$ C、 $\frac{E D}{B C} = \frac{D A}{A B}$ D、 $\frac{A E}{A D} = \frac{A C}{A B}$

查看试题解析
12. 如图所示，为了测量文昌塔AB的高度，数学兴趣小组根据光的反射定理（图中 $∠ 1 = ∠ 2$ ），把一面镜子放在点C处，然后观测者沿着直线BC后退到点D.这时恰好在镜子里看到塔顶A，此时量得 $C D = 4 m$ ， $B D = 94 m$ ，观测者目高 $E D = 1.6 m$ ，则塔AB的高度为（）

A、35m B、36m C、37m D、38m

查看试题解析

二、填空题

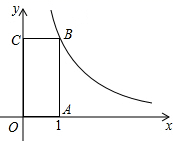
13. 方程 ${(x - 1)}^{2} = 9$ 的根是.

查看试题解析
14. 已知反比例函数 $y = \frac{m + 1}{x}$ 的图象具有下列特征：在所在象限内，y的值随x值的增大而增大.那么m的取值范围是.

查看试题解析
15. 三角形两边的长分别为2和5，第三边的长是方程 $x^{2} - 8 x + 15 = 0$ 的根，则该三角形的周长为 .

查看试题解析
16. 如图，点B在反比例函数 $y = \frac{3}{x}$ 的图象上，过点B分别向x轴，y轴作垂线，垂足分别为A，C，则矩形OABC的面积为.

查看试题解析
17. 如图，在 $△ A B C$ 中，EF∥BC， $A E = \frac{1}{2} B E$ ， $S_{四边形 B C F E} = 16$ ，则 $S_{△ A E F} =$ .

查看试题解析
18. 小明将3块拼图①、②、③拼成如图1所示一个矩形，也可以拼成如图2所示的“L”形状，且是轴对称图形.已知 $A B = 9$ ， $B C = 16$ ， $F G ⊥ A D$ ，则FG的长为.

查看试题解析

三、解答题

19. 解方程： $3 x^{2} + 4 x = - 1$ ．

查看试题解析
20. 已知反比例函数 $y = \frac{2 k + 1}{x}$ .

(1)、如果这个函数的图象经过点 $(2 ， - 1)$ ，求 $k$ 的值；

(2)、如果这个函数图象如图所示，求 $k$ 的取值范围.

查看试题解析
21. 关于 $x$ 的一元二次方程 $2 x^{2} - 4 x - k = 0$ 有两个不相等的实数根.

(1)、求k的取值范围；

(2)、若 $k = 1$ ，请用配方法求该方程的根.

查看试题解析
22. 如图，在 $Δ A B C$ 中，点 $D ， E$ 分别在边 $A B$ 、 $A C$ 上， $D C$ 与 $B E$ 相交于点 $O$ ，且 $D O = 2$ ， $B O = D C = 6$ ， $O E = 3$ .

(1)、求证： $Δ D O E ∽ Δ C O B$ ；

(2)、已知 $A D = 5$ ，求 $A B$ .

查看试题解析
23. 受各方面因素的影响，最近两年来某地平均房价由10000元/平方米，下降到8100元/平方米，如果在这两年里，年平均下降率相同.

(1)、求年平均下降率；

(2)、按照这个年平均下降率，预计下一年房价每平方米多少元？

查看试题解析
24. 如图，一次函数y＝ax＋b的图象与反比例函数 $y = \frac{k}{x}$ 的图象交于点A、B，与x轴交于点 $C (5 ， 0)$ ，若OC＝AC，且 $S_{△}_{O A C}$ ＝10

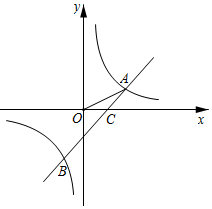(1)、求反比例函数与一次函数的表达式；

(2)、请直接写出不等式ax＋b＞ $\frac{k}{x}$ 的解集.

查看试题解析
25. 如图，已知 $△ A B C$ 和 $△ A D E$ 均为等腰三角形， $A C = B C$ ， $D E = A E$ .

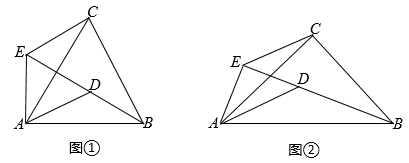(1)、问题发现：如图①，当 $∠ A C B = ∠ A E D = 60 °$ 时，点B、D、E在同一直线上，连接CE，请判断线段BD、CE之间的数量关系及 $∠ C E B$ 的度数，并说明理由：

(2)、拓展探究：如图②，当 $∠ A C B = ∠ A E D = 90 °$ 时，点B、D、E在同一直线上，连接CE，请判断线段BD、CE之间的数量关系及 $∠ C E B$ 的度数，并说明理由.

查看试题解析
26. 阅读材料：各类方程的解法：
求解一元一次方程，根据等式的基本性质，把方程转化为x=a的形式，求解二元一次方程组，把它转化为一元一次方程来解；类似的，三元一次方程组，把它转化为解二元一次方程组.求解一元二次方程，把它转化为两个一元一次方程来解.求解分式方程，把它转化为整式方程来解，由于“去分母”可能产生增根，所以解分式方程必须检验.各类方程的解法不尽相同，但是它们有一个共同的基本数学思想——转化，把未知转化为已知.

用“转化”的数学思想，我们还可以解一些新的方程.例如，一元三次方程x³+x²-2x=0，可以通过因式分解把它转化为 $x (x^{2} + x - 2) = 0$ ，解方程x=0和x²+x-2=0，可得方程x³+x²-2x=0的解.

(1)、问题：方程 $6 x^{3} + 14 x^{2} - 12 x = 0$ 的解是： $x_{1}$ =0， $x_{2}$ = ， $x_{3}$ =；

(2)、拓展：用“转化”思想求方程 $\sqrt{2 x + 3} = x$ 的解；

(3)、应用：如图，已知矩形草坪ABCD的长AD=21m，宽AB=8m，点P在AD上（AP＞PD），小华把一根长为27m的绳子一段固定在点B，把长绳PB段拉直并固定在点P，再拉直，长绳的另一端恰好落在点C，求AP的长.

查看试题解析