天津市南开区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-11-24 类型：期中考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点P（3，﹣1）关于坐标原点中心对称的点P的坐标是（）

A、（3，1） B、（﹣3，﹣1） C、（﹣3，1） D、（﹣1，3）

查看试题解析
2.
下列四个图形分别是四届国际数学家大会的会标，其中属于中心对称图形的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 一元二次方程 $3 x^{2} + 5 x + 1 = 0$ 根的情况是（）

A、没有实数根 B、有两个不相等的实数根 C、无法判断 D、有两个相等的实数根

查看试题解析
4. 关于二次函数 $y = 2 {(x - 4)}^{2} + 6$ 的最大值或最小值，下列说法正确的是（）

A、有最大值4 B、有最小值4 C、有最大值6 D、有最小值6

查看试题解析
5. 如图，四边形 $A B C D$ 为 $⊙ O$ 的内接四边形，若 $∠ A = 60 °$ ，则 $∠ C$ 等于（）

A、 $30 °$ B、 $60 °$ C、 $120 °$ D、 $300 °$

查看试题解析
6. 如图， $A ， B$ 是⊙O上的两个点， $B C$ 是弦，若 $∠ B = 32 °$ ，则 $∠ O A C =$ （）

A、 $64 °$ B、 $58 °$ C、 $68 °$ D、 $55 °$

查看试题解析
7. 如图， $A D$ 为⊙O的直径， $A D = 6 cm$ ， $∠ D A C = ∠ A B C$ ，则 $A C$ 的长度为（）

A、 $\sqrt{2}$ B、 $2 \sqrt{2}$ C、 $3 \sqrt{2}$ D、 $3 \sqrt{3}$

查看试题解析
8. 如图，在Rt△ABC中，∠BAC＝90°，将△ABC绕点A顺时针旋转90°后得到的△AB'C'（点B的对应点是点B'，点C的对应点是点C'），连接CC'．若∠CC'B'＝32°，则∠B的大小是（　　）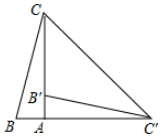

A、32° B、64° C、77° D、87°

查看试题解析
9. 已知⊙O的半径是4，点P到圆心O的距离d为方程x²﹣4x﹣5＝0的一个根，则点P在（　　）

A、⊙O的内部 B、⊙O的外部 C、⊙O上或⊙O的内部 D、⊙O上或⊙O的外部

查看试题解析
10. 如图，学校课外生物小组的试验园地的形状是长35米、宽20米的矩形．为便于管理，要在中间开辟一横两纵共三条等宽的小道，使种植面积为600平方米，则小道的宽为多少米？若设小道的宽为 $x$ 米，则根据题意，列方程为（）

A、 $35 \times 20 - 35 x - 20 x + 2 x^{2} = 600$ B、 $35 \times 20 - 35 x - 2 \times 20 x = 600$ C、 $(35 - 2 x) (20 - x) = 600$ D、 $(35 - x) (20 - 2 x) = 600$

查看试题解析
11. 如图，点A的坐标为（﹣3，2），⊙A的半径为1，P为坐标轴上一动点，PQ切⊙A于点Q ，在所有P点中，使得PQ长最小时，点P的坐标为（　　）

A、（0，2） B、（0，3） C、（﹣2，0） D、（﹣3，0）

查看试题解析
12. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值：

$x$

…

-2

0

1

3

…

$y$

…

6

-4

-6

-4

…

下列各选项中，正确的是

A、这个函数的图象开口向下 B、这个函数的图象与x轴无交点 C、这个函数的最小值小于-6 D、当 $x > 1$ 时，y的值随x值的增大而增大

查看试题解析

二、填空题

13. 已知关于x的方程x²+x+2a﹣4＝0的一个根是﹣1，则a的值是．

查看试题解析
14. 如图，将△ABC绕着点B逆时针旋转45°后得到△A'BC'，若∠A＝100°，∠C＝45°，则∠A'BC的度数为度．

查看试题解析
15. 已知抛物线与x轴只有一个交点，且抛物线的对称轴为直线x＝﹣1，请写出一个满足条件的抛物线的解析式．

查看试题解析
16. 抛物线 $y = - 2 {(x - 1)}^{2} + 3$ 向上平移1个单位后，再向右平移2个单位，得到的抛物线的解析式为．

查看试题解析
17. 如图，AB是半圆O的直径，点D在半圆O上，AB＝13，AD＝5，C是弧BD上的一个动点，连接AC ，过D点作DH⊥AC于H ．连接BH ，在点C移动的过程中，BH的最小值是．

查看试题解析
18. 如图，在平面直角坐标系中，A（0，4），B（4，4），C（6，2）．

（Ⅰ）若经过A、B、C三点的圆弧所在圆的圆心为M ，

点M的坐标为；⊙M的半径为；

（Ⅱ）若画出该圆弧所在圆，则在整个平面直角坐标系网格中该圆共经过个格点．

查看试题解析

三、解答题

19. 解一元二次方程

(1)、x²﹣4x＝0；

(2)、3x²﹣x﹣1＝0．

查看试题解析
20. 已知关于x的方程 $(k - 1) x^{2} - 2 x + 1 = 0$ 有两个实数根．

(1)、求k的取值范围；

(2)、当k取最大整数时，求此时方程的根．

查看试题解析
21. 已知二次函数y＝x²﹣4x+3．

(1)、将y＝x²﹣4x+3化成y＝a（x﹣h）²+k的形式：；

(2)、抛物线与x轴交点坐标为；

(3)、在平面直角坐标系中，画出这个二次函数的图象；

(4)、当y＜0时，x的取值范围是；

(5)、当0＜x＜3时，y的取值范围是．

查看试题解析
22. 已知⊙O中，弦AB⊥AC ，且AB＝AC＝8，点D在⊙O上，连接AD ， BD ， CD ．

(1)、如图1，若AD经过圆心O ，求BD ， CD的长；

(2)、如图2，若∠BAD＝2∠DAC ，求BD ， CD的长．

查看试题解析
23. 某水果超市经销一种高档水果，售价每千克50元．

(1)、若连续两次降价后每千克32元，且每次下降的百分率相同，求每次下降的百分率；
获得最大利润？最大利润是多少？

(2)、若按现售价销售，每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，超市决定采取适当的涨价措施，但超市规定每千克涨价不能超过8元，若每千克涨价1元，日销售量将减少20千克．现该超市希望每天盈利6000元，那么每千克应涨价多少元？

(3)、在（2）的基础上，利用函数关系式求出每千克水果涨价多少元时，超市每天可

查看试题解析
24. 把两个等腰直角△ABC和△ADE按如图1所示的位置摆放，将△ADE绕点A按逆时针方向旋转，如图2，连接BD ， EC ，设旋转角α（0°＜α＜360°）．

(1)、当DE⊥AC时，旋转角α＝度，AD与BC的位置关系是， AE与BC的位置关系是；

(2)、当点D在线段BE上时，求∠BEC的度数；

(3)、当旋转角α＝时，△ABD的面积最大．

查看试题解析
25. 如图1，抛物线y＝ax²+bx﹣8与x轴交于A（2，0），B（4，0），D为抛物线的顶点．

(1)、求抛物线的解析式；

(2)、如图2，若H为射线DA与y轴的交点，N为射线AB上一点，设N点的横坐标为t ， △DHN的面积为S ，求S与t的函数关系式；

(3)、如图3，在（2）的条件下，若N与B重合，G为线段DH上一点，过G作y轴的平行线交抛物线于F ，连接AF ，若NG=NQ ， NG⊥NQ ，且∠AGN＝∠FAG ，求F点的坐标．

查看试题解析

$x$	…	-2	0	1	3	…
$y$	…	6	-4	-6	-4	…