天津市津南区东部学区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-11-24 类型：期中考试

进入出卷网下载

一、单选题

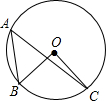
1. 将方程 $5 x^{2} - 1 = 4 x$ 化成一元二次方程的一般式，则一次项系数是（）

A、5 B、4 C、﹣4 D、﹣1

查看试题解析
2. 一元二次方程x²+x+6＝0的根的情况是（　　）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
3. 用配方法解方程x²﹣8x＋2＝0，配方后的方程是（）

A、（x﹣4）²＝14 B、（x﹣4）²＝2 C、（x﹣1）²＝6 D、（x﹣1）²＝﹣7

查看试题解析
4. 若方程5x²+x﹣5＝0的两个实数根分别为x₁ ， x₂ ．则x₁+x₂等于（　　）

A、 $- \frac{1}{5}$ B、 $\frac{1}{5}$ C、﹣1 D、1

查看试题解析
5. 关于x的一元二次方程 $x^{2} - 2 x + m = 0$ 有两个实数根，则m的取值范围是（　　）

A、m＞﹣1 B、m＞1 C、m≤1 D、m≤﹣1

查看试题解析
6. 对于抛物线y＝2（x﹣1）²+3的顶点坐标是（　　）

A、(1，3) B、(3，1) C、(﹣3，2) D、(2，3)

查看试题解析
7. 关于二次函数y＝x²﹣x的下列结论，错误的是（　　）

A、图象的开口向上 B、当x＜0时，y随x的增大而增大 C、图象经过点(2，2) D、图象的对称轴是直线x＝ $\frac{1}{2}$

查看试题解析
8. 如图，点A，B，C在⊙O上，∠A＝50°，则∠BOC的度数为（）

A、40° B、50° C、80° D、100°

查看试题解析
9. 下列说法正确的是（　　）

A、平分弦的直径垂直于弦 B、三个点确定一个圆 C、相等的圆心角所对的弧相等 D、圆内接四边形的对角互补

查看试题解析
10. 某中学九年级以班级为单位组织篮球比赛，每两班之间都要比赛一场，共比赛了15场，设参赛班级的个数为 $x$ ，则 $x$ 的值为（　　）

A、5 B、6 C、7 D、8

查看试题解析
11. 某种植基地2016年蔬菜产量为80吨，预计2018年蔬菜产量达到100吨，求蔬菜产量的年平均增长率，设蔬菜产量的年平均增长率为x，则可列方程为（）

A、80（1+x）²=100 B、100（1﹣x）²=80 C、80（1+2x）=100 D、80（1+x²）=100

查看试题解析
12. 已知二次函数y＝ax²+bx+c（a ， b ， c为常数，a≠0），其中，自变量x与函数值y之间满足下面对应关系：

x

……

$-$ 5

$-$ 3

$-$ 1

……

y＝ax²+bx+c

……

$-$ 2.5

1.5

1.5

……

则 $\frac{b (a + b + c)}{a}$ 的值是（　　）

A、﹣10 B、﹣5 C、﹣ $\frac{5}{2}$ D、﹣ $\frac{5}{4}$

查看试题解析

二、填空题

13. 方程 $4 x^{2} - 6 x = 0$ 的根为．

查看试题解析
14. 若m是方程2x²﹣3x﹣1＝0的一个根，则6m²﹣9m+2016的值为．

查看试题解析
15. 如图，AB是⊙O的直径，弦CD⊥AB于点E，OC=5cm，CD=8cm，则AE=cm．

查看试题解析
16. 把抛物线y＝ $\frac{1}{2} {(x + 2)}^{2} - 1$ 先向上平移2个单位长度，再向左平移1个单位长度，则平移后抛物线的解析式是．

查看试题解析
17. 如图，抛物线y＝ax²+bx+c（a＞0）的对称轴是直线x＝1，若点A(4，0)在该抛物线上，则4a﹣2b+c的值为．

查看试题解析
18. 已知二次函数y＝ax²+2ax+3a²+3（其中x是自变量），当x≥2时，y随x的增大而减小，且﹣2≤x≤1时，y的最大值为9，则a的值为．

查看试题解析

三、解答题

19. 解下列方程．

(1)、 $x^{2} + 10 x - 2 = 0$ （配方法）

(2)、3x²﹣6x﹣2＝0（公式法）

查看试题解析
20. 用因式分解法解方程

(1)、x（2x﹣5）＝2（2x﹣5）

(2)、4x²﹣4x+1＝（x+3）²

查看试题解析

21. 二次函数y＝ax²+bx+c（a≠0）的自变量x与对应的函数y的值（部分）如表所示：

x	…	﹣3	﹣2	﹣1	0	1	2	…
y	…	m	﹣2	﹣3	﹣2	1	6	…

解答下列问题：

(1)、表格中m的值等于；

(2)、求这个二次函数的解析式；

(3)、在直角坐标系中，画出这个函数的图象．

查看试题解析

22. 如图，四边形ABCD是⊙O的内接四边形，AD=CD ， ∠BAC＝70°，∠ACB＝50°．

(1)、求∠ABD的度数；

(2)、求∠BAD的度数．

查看试题解析
23. 已知点A ，点B ，点C在⊙O上，∠CAB的平分线交⊙O于点D ．

(1)、如图①，若BC为⊙O的直径，求∠CBD的大小；

(2)、如图②，若∠CAB＝60°，BD=5，求⊙O半径．

查看试题解析
24. 如图①，在一幅矩形地毯的四周镶有宽度相同的花边．如图②，地毯中央的矩形图案长6m、宽3m，整个地毯的面积是40m² ，求花边的宽．

(1)、设花边的宽为xm，用含x的代数式表示：
矩形地毯ABCD的长为m；

矩形地毯ABCD的宽为m；

矩形地毯ABCD的面积为m²；

(2)、列出方程，并求出问题的解．

查看试题解析
25. 某商品的进价为每件40元，售价为每件60元，每周可卖出300件．如果每件商品的售价每降价1元，每周可多卖20件（每件售价不能低于40元）．设每件商品的售价下降x元（x为正整数），每周的销售利润为y元．

(1)、求y与x的函数关系式，并直接写出自变量x的取值范围；

(2)、每件商品的售价定为多少元时，每周可获得最大利润？最大的周利润是多少元？

(3)、每件商品的售价定为多少元时，每周的利润恰好是5280元？

查看试题解析
26. 已知抛物线 $y = - \frac{1}{2} x^{2} + \frac{3}{2} x + 2$ ，与x轴交于两点A ， B（点A在点B的左侧），与y轴交于点C ．

(1)、求点A ， B和点C的坐标；

(2)、已知P是线段 $B C$ 上的一个动点．

①若 $P Q ⊥ x$ 轴，交抛物线于点Q，当 $B P + P Q$ 取最大值时，求点P的坐标；

②求 $\sqrt{2} A P + P B$ 的最小值．

查看试题解析

x	……	$-$ 5	$-$ 3	$-$ 1	……
y＝ax²+bx+c	……	$-$ 2.5	1.5	1.5	……