天津市津南区北部学区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-11-24 类型：期中考试

进入出卷网下载

一、单选题

1. 将方程 $5 x^{2} - 1 = 4 x$ 化成一元二次方程的一般式，则一次项系数是（）

A、5 B、4 C、﹣4 D、﹣1

查看试题解析
2. 一元二次方程x²+x+6＝0的根的情况是（　　）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
3. 用配方法解方程x²﹣8x＋2＝0，配方后的方程是（）

A、（x﹣4）²＝14 B、（x﹣4）²＝2 C、（x﹣1）²＝6 D、（x﹣1）²＝﹣7

查看试题解析
4. 若方程3x²＋7x﹣9＝0的两个实数根分别为x₁ ， x₂ ，则x₁x₂等于（）

A、 $- \frac{7}{3}$ B、 $\frac{7}{3}$ C、﹣3 D、3

查看试题解析
5. 已知关于x的一元二次方程(m－1)x²＋2x＋1＝0有实数根，则m的取值范围是（）

A、m＜2 B、m≤2 C、m＜2且m≠1 D、m≤2且m≠1

查看试题解析
6. 抛物线y＝ $\frac{1}{2}$ （x﹣1）²＋2的顶点坐标是（）

A、（1，2） B、（2，1） C、（﹣1，2） D、（2，﹣1）

查看试题解析
7. 如图，四边形ABCD内接于⊙O ，若它的一个外角∠DCE＝65°，∠ABC＝68°，则∠A的度数为（　　）.

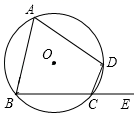A、112° B、68° C、65° D、52°

查看试题解析
8. 把抛物线 $y = \frac{1}{2} {(x + 2)}^{2} - 1$ 向上平移2个单位长度，则平移后抛物线的解析式是（）

A、 $y = \frac{1}{2} x^{2} - 1$ B、 $y = \frac{1}{2} {(x + 2)}^{2}$ C、 $y = \frac{1}{2} {(x + 2)}^{2} + 1$ D、 $y = \frac{1}{2} {(x + 4)}^{2} - 1$

查看试题解析
9. 如图，⊙O中，弦AB、CD相交于点P，若∠A＝30°，∠APD＝70°，则∠B等于（）

A、30° B、35° C、40° D、50°

查看试题解析
10. 要组织一次篮球联赛，赛制为单循环形式（每两队之间都赛一场），计划安排21场比赛，应邀请多少个队参加比赛．设应邀请x个队参加比赛，则x的值为（）

A、7 B、8 C、9 D、10

查看试题解析
11. 如图，把一块长为40cm，宽为30cm的矩形硬纸板的四角剪去四个相同小正方形，然后把纸板的四边沿虚线折起，并用胶带粘好，即可做成一个无盖纸盒.若该无盖纸盒的底面积为600cm² ，设剪去小正方形的边长为xcm，则可列方程为（）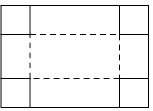

A、（30﹣2x）（40﹣x）＝600 B、（30﹣x）（40﹣x）＝600 C、（30﹣x）（40﹣2x）＝600 D、（30﹣2x）（40﹣2x）＝600

查看试题解析
12. 已知二次函数y＝ax²＋bx＋c中，其函数y与自变量x之间的部分对应值如下表所示：

x

…

0

1

2

3

4

…

y

…

4

1

0

1

4

…

点A(x₁ ， y₁)、B(x₂ ， y₂)在函数的图象上，则当1＜x₁＜2，3＜x₂＜4时，y₁与y₂的大小关系正确的是（）

A、y₁＞y₂ B、y₁＜y₂ C、y₁≥y₂ D、y₁≤y₂

查看试题解析

二、填空题

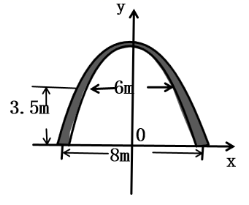
13. 方程x²+x=0的解是．

查看试题解析
14. 已知2是方程x²﹣4x＋m＝0的一个实数根，则实数m的值是．

查看试题解析
15. 抛物线 $y = x^{2} + 3 x + 2$ 的对称轴是直线．

查看试题解析
16. 小强用一根10m长的铁丝围成了一个面积为6m²的矩形，则这个矩形较大边的长是m．

查看试题解析
17. 如图，某大门的形状是一抛物线形建筑，大门的地面宽8m，在两侧距地面3.5m高处有两个挂单位名牌匾用的铁环，两铁环的水平距离是6m．若按图所示建立平面直角坐标系，则抛物线的解析式是．（建筑物厚度忽略不计）

查看试题解析
18. 如图，抛物线y＝ax²﹣x﹣ $\frac{3}{2}$ 与x轴正半轴交于点A（3，0）．以OA为边在x轴上方作正方形OABC ，延长CB交抛物线于点D ，再以BD为边向上作正方形BDEF ．

(1)、a的值为；

(2)、点F的坐标是．

查看试题解析

三、解答题

19. 解下列方程．

(1)、 $x^{2} + 10 x - 2 = 0$ （配方法）

(2)、3x²﹣6x﹣2＝0（公式法）

查看试题解析
20. 用因式分解法解方程．

(1)、 $x^{2} + 4 x - 21 = 0$

(2)、 ${(2 x - 1)}^{2} - {(x + 3)}^{2} = 0$

查看试题解析

21. 已知二次函数

y = \frac{1}{2} {(x + 2)}^{2} - 2

．

(1)、填写表中空格处的数值：

x	…	﹣5	﹣4	﹣3	﹣2	﹣1	0	1	…
$y = \frac{1}{2} {(x + 2)}^{2} - 2$	…	$\frac{5}{2}$			﹣2	$- \frac{3}{2}$	0		…

(2)、画出这个函数的图象．

查看试题解析

22. 如图，在⊙O中，点C是 $\overset{⌢}{A B}$ 的中点，弦AB与半径OC相交于点D，AB=12，CD=2.求⊙O半径的长.

查看试题解析
23.
如图，CD是⊙O的直径，点A在DC的延长线上，∠A=20°，AE交⊙O于点B，且AB=OC．

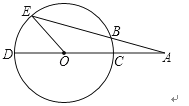(1)、求∠AOB的度数

(2)、求∠EOD的度数

查看试题解析
24. 抛物线 $y = x^{2} + b x + c$ 经过（﹣1，3），（2，6）两点．

(1)、求这条抛物线的解析式；

(2)、求这条抛物线的顶点坐标；

(3)、将此抛物线向上平移1个单位长，再向左平移2个单位长，得到抛物线C₁ ，写出抛物线C₁的解析式．

查看试题解析
25. 某商品的进价为每件40元，售价为每件60元，每周可卖出300件．如果每件商品的售价每降价1元，每周可多卖20件（每件售价不能低于40元）．设每件商品的售价下降x元（x为正整数），每周的销售利润为y元．

(1)、求y与x的函数关系式，并直接写出自变量x的取值范围；

(2)、每件商品的售价定为多少元时，每周可获得最大利润？最大的周利润是多少元？

(3)、每件商品的售价定为多少元时，每周的利润恰好是5280元？

查看试题解析
26. 已知抛物线y＝x²﹣（m﹣1）x﹣m（m是常数）与x轴交于点A（x₁ ， 0）和点B（x₂ ， 0），（x₁＜x₂），与y轴交于点C ，顶点为P ．

(1)、当抛物线的对称轴为直线x＝1时，
①求抛物线顶点P的坐标；

②求△ABC的面积；

(2)、当点A、B位于点（1，0）两侧时，
①求点A的坐标；

②若 $x > \frac{1}{2}$ ，函数值满足y随x的增大而增大，求m的取值范围．

查看试题解析