上海市普陀区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-11-24 类型:期中考试
一、单选题
-
1. 下列函数中,属于二次函数的是( )A、 B、 C、 D、2. 已知抛物线 ,a是常数,且 ,下列选项中可能是它大致图像的是( )A、
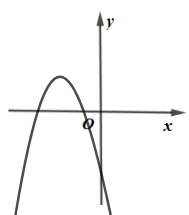 B、
B、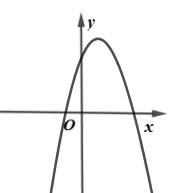 C、
C、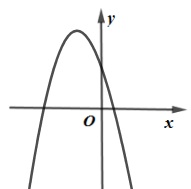 D、
D、 3. 下列关于向量的说法中,错误的是( )A、 B、如果 ,那么 C、 是非零向量, 是单位向量,那么 D、4. 下列各组条件中,一定能够判定 与 相似的是( )A、 , ; B、 , , , ; C、 三边长分别为 , , , 三边之比为 ; D、 , , .5. 如图,已知 , 与 相交于点O,点G是 的中点,过点G作 交 于点E,如果 , ,那么 等于( )
3. 下列关于向量的说法中,错误的是( )A、 B、如果 ,那么 C、 是非零向量, 是单位向量,那么 D、4. 下列各组条件中,一定能够判定 与 相似的是( )A、 , ; B、 , , , ; C、 三边长分别为 , , , 三边之比为 ; D、 , , .5. 如图,已知 , 与 相交于点O,点G是 的中点,过点G作 交 于点E,如果 , ,那么 等于( )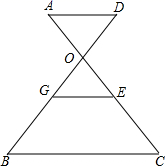 A、 B、 C、 D、6. 如图,在 中, 是边 上的高,那么下列条件不一定能推出 的选项是( )
A、 B、 C、 D、6. 如图,在 中, 是边 上的高,那么下列条件不一定能推出 的选项是( )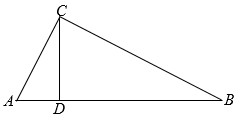 A、 ; B、 ; C、 ; D、 .
A、 ; B、 ; C、 ; D、 .二、填空题
-
7. 已知 ,那么 .8. 已知点 是线段 的黄金分割点,且 ,如果 ,那么 .9. 如图,直线 ,它们依次交直线m、n于点A、C、E和B、D、F,已知 , , ,那么 等于 .
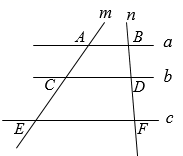 10. 将抛物线y=2 (x+1)2-3向右平移2个单位,再向上平移3个单位,则所得抛物线的表达式为 .11. 已知次函数 的一个函数值是2,那么对应的自变量x的值是 .12. 用“描点法”画二次函数 的图像时,列出了下面的表格:
10. 将抛物线y=2 (x+1)2-3向右平移2个单位,再向上平移3个单位,则所得抛物线的表达式为 .11. 已知次函数 的一个函数值是2,那么对应的自变量x的值是 .12. 用“描点法”画二次函数 的图像时,列出了下面的表格:0
1
1
根据表格上的信息回答问题:当 时, .
13. 如果向量 与单位向量 方向相反,且长度为 ,那么 . (用 表示)14. △ABC中,AD是中线,G是重心, ,那么 =(用 表示).15. 如图,矩形 的边 在 的边 上,顶点G、F分别在边 、 上,已知 , , ,那么边 上的高的长是 .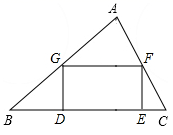 16. 如图,在 中,D是 上一点, , , ,如果 ,那么 的面积是 .
16. 如图,在 中,D是 上一点, , , ,如果 ,那么 的面积是 .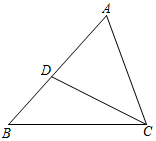 17. 如图,在平行四边形 中,过点A作 ,垂足为E,联结 ,F为线段 上一点,且 ,如果 , , ,那么 的长为 .
17. 如图,在平行四边形 中,过点A作 ,垂足为E,联结 ,F为线段 上一点,且 ,如果 , , ,那么 的长为 .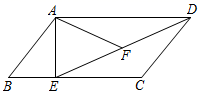 18. 在 中, , , ,点D、E分别在边 、 上,且 , ,将 绕点B旋转至 ,点D、E分别对应点 、 ,当 、 、 三点共线时, 的长为 .
18. 在 中, , , ,点D、E分别在边 、 上,且 , ,将 绕点B旋转至 ,点D、E分别对应点 、 ,当 、 、 三点共线时, 的长为 .三、解答题
-
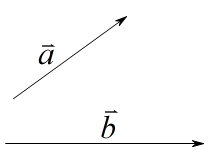
19. 如图,已知向量 、 ,求作向量 ,满足 .(不要求写作法,但要保留作图痕迹,并写出结论)
 20. 已知二次函数 的图像经过 、 , .(1)、求这个二次函数的解析式;(2)、如果点 和点 在函数图象上,那么当 时,请直接写出 与 的大小关系: .21. 在平面直角坐标系 中,已知抛物线 .(1)、写这条抛物线的开口方向、顶点坐标,并说明它的变化情况;(2)、我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”.试求抛物线 的“不动点”的坐标.22. 如图,已知 ,A是 上一点, , 交 于D, 交 于E,连接 .
20. 已知二次函数 的图像经过 、 , .(1)、求这个二次函数的解析式;(2)、如果点 和点 在函数图象上,那么当 时,请直接写出 与 的大小关系: .21. 在平面直角坐标系 中,已知抛物线 .(1)、写这条抛物线的开口方向、顶点坐标,并说明它的变化情况;(2)、我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”.试求抛物线 的“不动点”的坐标.22. 如图,已知 ,A是 上一点, , 交 于D, 交 于E,连接 . (1)、求证: ;(2)、设 与 的交点为点G,如果 , ,求 的值.23. 如图,在等腰直角 中, , ,过点C作射线 ,D为射线 上一点,E在边 上(不与B、C重合)且 , 与 交于点O.
(1)、求证: ;(2)、设 与 的交点为点G,如果 , ,求 的值.23. 如图,在等腰直角 中, , ,过点C作射线 ,D为射线 上一点,E在边 上(不与B、C重合)且 , 与 交于点O. (1)、求证: ;(2)、如果 ,求证: .
(1)、求证: ;(2)、如果 ,求证: .