山西省吕梁市交城县2021-2022学年九年级上学期期中考试数学试题
试卷更新日期:2021-11-24 类型:期中考试
一、单选题
-
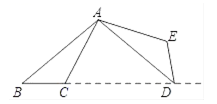
1. 下列方程中,是一元二次方程的是( )A、 B、 C、 D、2. 请判断一元二次方程 的实数根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定3. 下列二次函数中,其图象的顶点坐标为(-3,-1)的是( )A、 B、 C、 D、4. 如图,将△ABC绕点A逆时针旋转100°,得到△ADE.若点D在线段BC的延长线上,则 的大小为( )
 A、30° B、40° C、50° D、60°5. 若关于x的一元二次方程 可以通过配方写成 的形式,那么下列关于 的值正确的是( )A、 B、 C、 D、6. 如图,四边形ABCD中,AB=AD , CE⊥BD , CE= BD . 若△ABD的周长为20cm,则△BCD的面积S(cm2)与AB的长x(cm)之间的函数关系式可以是( )
A、30° B、40° C、50° D、60°5. 若关于x的一元二次方程 可以通过配方写成 的形式,那么下列关于 的值正确的是( )A、 B、 C、 D、6. 如图,四边形ABCD中,AB=AD , CE⊥BD , CE= BD . 若△ABD的周长为20cm,则△BCD的面积S(cm2)与AB的长x(cm)之间的函数关系式可以是( )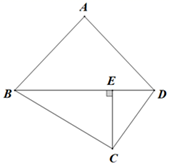 A、 B、 C、 D、7. 将抛物线 向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为( )A、 B、 C、 D、8. 如图是二次函数 的部分图象,由图象可知不等式 的解集是( )
A、 B、 C、 D、7. 将抛物线 向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为( )A、 B、 C、 D、8. 如图是二次函数 的部分图象,由图象可知不等式 的解集是( ) A、 B、 C、 D、 或9. 小希同学有一块长12cm,宽10cm的矩形卡纸,准备制作一个无盖的小礼盒.如图,她将矩形卡纸的四个角各剪掉一个边长为 cm的正方形后,剩余的部分刚好能围成一个底面积为48cm2的无盖长方体小礼盒.根据题意可列方程为( )
A、 B、 C、 D、 或9. 小希同学有一块长12cm,宽10cm的矩形卡纸,准备制作一个无盖的小礼盒.如图,她将矩形卡纸的四个角各剪掉一个边长为 cm的正方形后,剩余的部分刚好能围成一个底面积为48cm2的无盖长方体小礼盒.根据题意可列方程为( )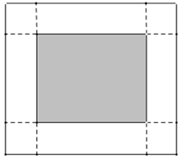 A、 B、 C、 D、10. 二次函数 ( )的图象如图所示,下列说法中错误的是( )
A、 B、 C、 D、10. 二次函数 ( )的图象如图所示,下列说法中错误的是( )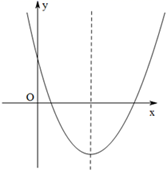 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 请写出一个与y轴交点为(0,5),对称轴为直线x=-1的抛物线的解析式(只需写一个).12. 如图,AB是⊙O的直径,C、D为半圆的三等分点,CE⊥AB于点E,∠ACE的度数为 .
 13. 飞机着陆后滑行的距离s(米)关于滑行的时间t(秒)的函数的解析式是 ,飞机着陆后滑行时间为秒才能停下来.14. 某校为了在学生中进行党史教育,决定在操场举行“中国共产党历史知识展览”,需要一块面积为480平方米的矩形场地.若矩形场地的一边靠墙(墙的长度足够),另外三边由总长为60米的围绳围成,并且在垂直于墙的边上各设置了一个开口宽为1米的入口和出口(如图).请根据方案计算出矩形场地的长米.
13. 飞机着陆后滑行的距离s(米)关于滑行的时间t(秒)的函数的解析式是 ,飞机着陆后滑行时间为秒才能停下来.14. 某校为了在学生中进行党史教育,决定在操场举行“中国共产党历史知识展览”,需要一块面积为480平方米的矩形场地.若矩形场地的一边靠墙(墙的长度足够),另外三边由总长为60米的围绳围成,并且在垂直于墙的边上各设置了一个开口宽为1米的入口和出口(如图).请根据方案计算出矩形场地的长米.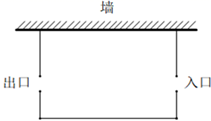 15. 如图,抛物线 与直线 交于A(-1,m),B(3,n)两点,则不等式 的解集是 .
15. 如图,抛物线 与直线 交于A(-1,m),B(3,n)两点,则不等式 的解集是 .
三、解答题
-
16. 解下列方程:(1)、(2)、17. 如图,D是等腰三角形ABC底边的中点,过点A、B、D作 .
 (1)、求证:AB是 的直径;(2)、延长CB交 于点E , 连接DE , 求证:DC=DE .18. 已知关于x的一元二次方程 .(1)、求证:该一元二次方程总有两个不相等的实数根;(2)、若该方程的两个根 是一个矩形的一边长和对角线的长,且矩形的另一边长为3,试求k的值.19. 按要求完成下列任务:
(1)、求证:AB是 的直径;(2)、延长CB交 于点E , 连接DE , 求证:DC=DE .18. 已知关于x的一元二次方程 .(1)、求证:该一元二次方程总有两个不相等的实数根;(2)、若该方程的两个根 是一个矩形的一边长和对角线的长,且矩形的另一边长为3,试求k的值.19. 按要求完成下列任务: (1)、用配方法把二次函数 写成 的形式;(2)、在下面的平面直角坐标系中画出 的图象;(3)、若A , B 是函数 图象上两点,且 ,请比较 , 的大小关系(直接写出结果);(4)、观察函数的图象:请回答x为何值时,y随x的增大而减小 ?这个问题的解答体现了什么数学思想?20. 请阅读下列材料,并按要求完成相应的任务:
(1)、用配方法把二次函数 写成 的形式;(2)、在下面的平面直角坐标系中画出 的图象;(3)、若A , B 是函数 图象上两点,且 ,请比较 , 的大小关系(直接写出结果);(4)、观察函数的图象:请回答x为何值时,y随x的增大而减小 ?这个问题的解答体现了什么数学思想?20. 请阅读下列材料,并按要求完成相应的任务:人类对一元二次方程的研究经历了漫长的岁月.一元二次方程及其解法最早出现在公元前两千年左右的古巴比伦人的《泥板文书》中.到了中世纪,阿拉伯数学家花拉子米在他的代表作《代数学》中给出了一元二次方程的一般解法,并用几何法进行了证明.我国古代三国时期的数学家赵爽也给出了类似的几何解法.赵爽在其所著的《勾股圆方图注》中记载了解方程 即 得方法.首先构造了如图1所示得图形,图中的大正方形面积是 ,其中四个全等的小矩形面积分别为 ,中间的小正方形面积为 ,所以大正方形的面积又可表示为 ,据此易得 .
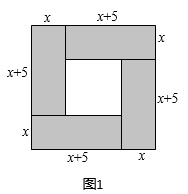

任务:
(1)、参照上述图解一元二次方程的方法,请在下面三个构图中选择能够说明方程 的正确构图是(从序号①②③中选择).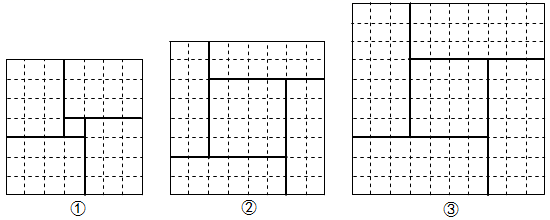 (2)、请你通过上述问题的学习,在图2的网格中设计正确的构图,用几何法求解方程 (写出必要的思考过程).21. 为了防控疫情的需要,某商店以每箱30元的价格购进一批消毒液.已知该商店第一天卖出消毒液80箱,每箱能获得10元的利润.后调查了解到:若每箱利润增加1元,每天就少卖4箱.某天该商店通过销售这批消毒液一共获得利润900元,则这天每箱消毒液的售价是多少元?22. 综合与实践
(2)、请你通过上述问题的学习,在图2的网格中设计正确的构图,用几何法求解方程 (写出必要的思考过程).21. 为了防控疫情的需要,某商店以每箱30元的价格购进一批消毒液.已知该商店第一天卖出消毒液80箱,每箱能获得10元的利润.后调查了解到:若每箱利润增加1元,每天就少卖4箱.某天该商店通过销售这批消毒液一共获得利润900元,则这天每箱消毒液的售价是多少元?22. 综合与实践
(情境呈现)
如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°.若固定△ABC , 将△DEC绕着点C旋转.
(1)、(初步探究)如图2,当△DEC绕点C旋转,点D恰好落在AB边的中点上时,请求出此时旋转角的度数.
(2)、如图2,当△DEC绕点C旋转,点D恰好落在AB边上时,若此时旋转角为 ,则∠CED的度数为(用含 的式子表示) .(3)、(拓展提升)当△DEC绕点C旋转到如图3所示的位置时,勤勉小组猜想:△BDC的面积与△AEC的面积相等,试判断勤勉小组的猜想是否符合题意,若符合题意,请你帮他们证明;若不符合题意,请说明理由.
23. 如图1,抛物线 与x轴交于A , B(3,0)两点,与y轴交于C(0,-2),直线AD交y轴于点E ,与抛物线交于A , D两点,点P是直线AD下方抛物线上一点(不与A , D重合). (1)、求抛物线的解析式与直线AD的解析式;(2)、如图1,过点P作PN∥y轴交直线AD于点N , 求线段PN的最大值;(3)、如图2,连接AP , DP , 是否存在点P , 使得三角形APD的面积等于2,若存在,求出此时点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式与直线AD的解析式;(2)、如图1,过点P作PN∥y轴交直线AD于点N , 求线段PN的最大值;(3)、如图2,连接AP , DP , 是否存在点P , 使得三角形APD的面积等于2,若存在,求出此时点P的坐标;若不存在,请说明理由.