山东省济南市章丘区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-11-24 类型：期中考试

进入出卷网下载

一、单选题

1. 矩形具有而菱形不具有的性质是( )

A、两组对边分别平行 B、对角线相等 C、对角线互相平分 D、两组对角分别相等

查看试题解析
2. 若关于x的一元二次方程kx²﹣2x﹣1＝0有两个不相等的实数根，则k的取值范围是（　　）

A、k＞1 B、k＞﹣1且k≠0 C、k＜1 D、k＜1且k≠0

查看试题解析
3. 用配方法解一元二次方程 $x^{2} - 4 x = 5$ 时，此方程可变形为（）

A、 ${(x + 2)}^{2} = 1$ B、 ${(x - 2)}^{2} = 1$ C、 ${(x + 2)}^{2} = 9$ D、 ${(x - 2)}^{2} = 9$

查看试题解析
4. 三角形两边长分别为3和6，第三边的长是方程x²﹣13x+36=0的两根，则该三角形的周长为（　　）

A、13 B、15 C、18 D、13或18

查看试题解析
5. 顺次连接矩形四边中点所得的四边形一定是（）

A、正方形 B、矩形 C、菱形 D、等腰梯形

查看试题解析
6. 如图，在四边形 $A B C D$ 中，如果 $∠ A D C = ∠ B A C$ ，那么下列条件中不能判定 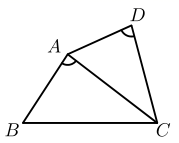$△ A D C$ 和 $△ B A C$ 相似的是（）

A、 $∠ D A C = ∠ A B C$ B、 $C A$ 是 $∠ B C D$ 的平分线 C、 $\frac{A D}{A B} = \frac{D C}{A C}$ D、 $A C^{2} = B C \cdot C D$

查看试题解析
7. 若 $x = - 1$ 是方程 $x^{2} + 3 x + c = 0$ 的一个根，则方程的另一个根为（）

A、 $x = 2$ B、 $x = - 2$ C、 $x = 4$ D、 $x = - 4$

查看试题解析
8. 某种花卉每盆的盈利与每盆的株数有一定的关系，每盆植3株时，平均每株盈利4元．若每盆增加1株，平均每株盈利减少0.5元，要使每盆的盈利达到15元，每盆应多植多少株？设每盆多植x株，则可以列出的方程是（　　）

A、（3+x）（4﹣0.5x）＝15 B、（x+3）（4+0.5x）＝15 C、（x+4）（3﹣0.5x）＝15 D、（x+1）（4﹣0.5x）＝15

查看试题解析
9. 若一个袋子中装有形状与大小均完全相同的4张卡片，4张卡片上分别标有数字﹣2，﹣1，2，3，现从中任意抽出其中两张卡片分别记为x，y，并以此确定点P（x，y），那么点P落在直线y=﹣x+1上的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
10. 如图，正方形ABCD的边长为4，G是BC边上一点，若矩形DEFG的边EF经过点A ， GD＝5，则FG长为（　　）

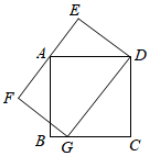A、2.8 B、3 C、3.2 D、4

查看试题解析
11. 如图，在等腰△ABC中，∠ABC＝∠ACB＝α，BC＝12，点D是边AB上一点，且BD＝4，点P是边BC上一动点，作∠DPE＝α，射线PE交边AC于点E ，当CE＝9时，则满足条件的P点的个数是（）

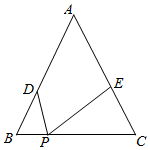A、1 B、2 C、3 D、以上都有可能

查看试题解析
12. 如图，已知菱形ABCD的两条对角线分别为6和8，M、N分别是边BC、CD的中点，P是对角线BD上一点，则PM+PN的最小值是（　　）

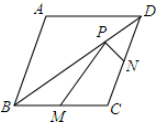A、5 B、10 C、6 D、8

查看试题解析

二、填空题

13. 已知 $\frac{a}{3} = \frac{b}{2}$ ，则 $\frac{a - b}{b}$ 的值是．

查看试题解析
14. 已知关于x的一元二次方程（a－1）x²－x + a²－1=0的一个根是0，那么a的值为.

查看试题解析
15. 某商品经过连续两次降价，销售单价由原来的125元降到80元，则平均每次降价的百分率为．

查看试题解析
16. 在▱ABCD中，E是AD上一点，且点E将AD分为2：3的两部分，连接BE、AC相交于F，则 $S_{Δ A E F} ： S_{Δ C B F}$ 是．

查看试题解析
17. 如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，H是AF的中点，那么CH的长是．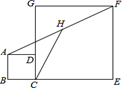

查看试题解析
18. 如图，点B₁在直线l：y＝ $\frac{1}{2}$ x上，点B₁的横坐标为2，过点B₁作B₁A₁⊥l ，交x轴于点A₁ ，以A₁B₁为边，向右作正方形A₁B₁B₂C₁ ，延长B₂C₁交x轴于点A₂；以A₂B₂为边，向右作正方形A₂B₂B₃C₂ ，延长B₃C₂交x轴于点A₃；以A₃B₃为边，向右作正方形A₃B₃B₄C₃ ，延长B₄C₃交x轴于点A₄；…；照这个规律进行下去，则第n个正方形A_nB_nB_n₊₁C_n的边长为（结果用含正整数n的代数式表示）．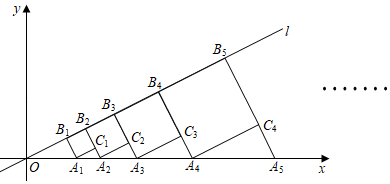

查看试题解析

三、解答题

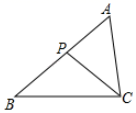
19. 解方程：

(1)、x²﹣4x﹣5＝0；

(2)、2x（x+1）＝x+1．

查看试题解析
20. 如图，在△ABC中，点P在AB边上，∠ABC＝∠ACP ．若AP＝4，AB＝9，求AC的长．

查看试题解析
21. 如图，菱形 $A B C D$ 的对角线 $A C ， B D$ 相交于点 $O ，$ 且 $D E / / A C ， A E / / B D$ ．求证：四边形 $A O D E$ 是矩形．

查看试题解析
22. 如图所示，某幼儿园有一道长为16米的墙，计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD．求该矩形草坪BC边的长．

查看试题解析
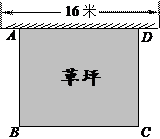23. 如图，△ABC是一块锐角三角形余料，边BC＝120mm，高AD＝80mm，要把它加工成矩形零件PQMN ，使一边在BC上，其余两个顶点分别在边AB、AC上．

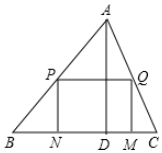(1)、求证：△APQ∽△ABC；

(2)、若这个矩形的边PN：PQ＝2：1，则这个矩形的长、宽各是多少？

查看试题解析
24. 某校开设了书画、器乐、戏曲、棋类四类兴趣课程，为了解全校学生对每类课程的选择情况，随机抽取了若干名学生进行调查（每人必选且只能选一类）.现将调查结果绘制成如下两幅不完整的统计图：

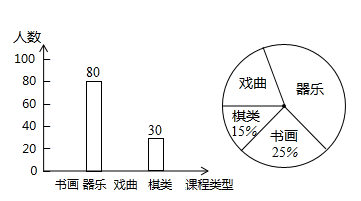(1)、本次随机调查抽取了多少名学生？

(2)、补全条形统计图中“书画”“戏曲”的空缺部分；

(3)、若该校共有1600名学生，请估计全校选择“戏曲”课程的学生有多少名；

(4)、学校从这四类课程中随机抽取两类参加“全市青少年才艺展示活动”，用列表或画树状图的方法求出恰好抽到“器乐”和“戏曲”课程的概率.（书画、器乐、戏曲、棋类可分别用字母 $A$ ， $B$ ， $C$ ， $D$ 表示）

查看试题解析
25. 如图，在长方形ABCD中，边AB、BC的长（AB＜BC）是方程x²-7x+12=0的两个根.点P从点A出发，以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动，运动时间为t（秒）.

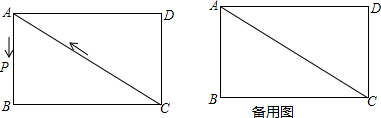(1)、求AB与BC的长；

(2)、当点P运动到边BC上时，试求出使AP长为 $\sqrt{10}$ 时运动时间t的值；

(3)、当点P运动到边AC上时，是否存在点P，使△CDP是等腰三角形？若存在，请求出运动时间t的值；若不存在，请说明理由.

查看试题解析
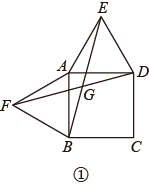
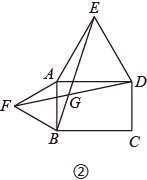
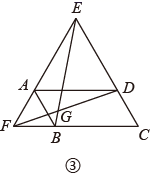26. 如图，以四边形 $A B C D$ 的边 $A B$ ， $A D$ 为边分别向外侧作等边三角形 $A B F$ 和等边三角形 $A D E$ ，连接 $E B$ ， $F D$ 相交于点G．

(1)、当四边形 $A B C D$ 为正方形时（如图①）， $E B$ 和 $F D$ 的数量关系是．（不用证明）

(2)、当四边形 $A B C D$ 为矩形时（如图②）， $E B$ 和 $F D$ 具有怎样的数量关系？并加以证明．

(3)、四边形 $A B C D$ 由正方形到矩形再到一般平行四边形的变化过程中， $∠ E G D$ 是否发生变化？如果改变，请说明理由；如果不变，请在图③中求出 $∠ E G D$ 的度数．

查看试题解析
27. 如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC ， GF⊥CD ．

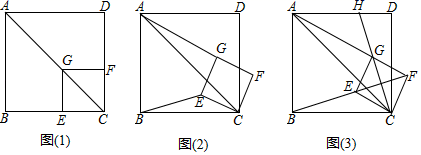(1)、①求证：四边形CEGF是正方形；
②推断： $\frac{AG}{BE}$ 的值为　▲　：

(2)、将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系；

(3)、正方形CEGF在旋转过程中，当B ， E ， F三点在一条直线上时，如图（3）所示，延长CG交AD于点H ．若AG＝6，GH＝2 $\sqrt{2}$ ，求正方形CEGF和正方形ABCD的边长．

查看试题解析