山东省滨州市博兴县2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-11-24 类型：期中考试

进入出卷网下载

一、单选题

1. 一元二次方程x²＝2x的根为（　　）

A、x＝0 B、x＝2 C、x＝0或x＝﹣2 D、x＝0或x＝2

查看试题解析
2. 一元二次方程 $x^{2} - 4 x - 1 = 0$ 配方后可化为（）

A、 ${(x + 2)}^{2} = 3$ B、 ${(x + 2)}^{2} = 5$ C、 ${(x - 2)}^{2} = 3$ D、 ${(x - 2)}^{2} = 5$

查看试题解析
3. 如果关于x的一元二次方程 $k x^{2} - 3 x + 1 = 0$ 有两个实数根，那么 $k$ 的取值范围是（）

A、 $k ⩾ \frac{9}{4}$ B、 $k ⩾ - \frac{9}{4}$ 且 $k \neq 0$ C、 $k ⩽ \frac{9}{4}$ 且 $k \neq 0$ D、 $k ⩽ - \frac{9}{4}$

查看试题解析
4. 已知抛物线 $y = - x^{2} + b x + 4$ 经过 $(- 2, n)$ 和 $(4, n)$ 两点，则n的值为（）

A、﹣2 B、﹣4 C、2 D、4

查看试题解析
5. 将抛物线 $y = x^{2} - 6 x + 5$ 向上平移两个单位长度，再向右平移一个单位长度后，得到的抛物线解析式是（）

A、 $y = {(x - 4)}^{2} - 6$ B、 $y = {(x - 1)}^{2} - 3$ C、 $y = {(x - 2)}^{2} - 2$ D、 $y = {(x - 4)}^{2} - 2$

查看试题解析
6. 二次函数 y=ax²+bx+c 部分图象如图所示，则下列结论中正确的是（）

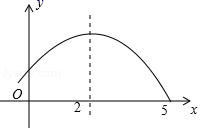A、a＞0 B、当 x＞2 时，y 随 x 的增大而增大 C、不等式 ax²+bx+c＞0 的解集是﹣1＜x＜5 D、a﹣b+c＞0

查看试题解析
7. 如图，在Rt△ABC中，∠C=90°，∠A=30°，AC=10．将直线CB绕着点C顺时针方向旋转，旋转过程中与边AB交于点D ，当旋转15°时，△ACD的面积为（）

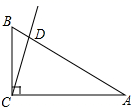A、25 B、25 $\sqrt{3}$ C、50 D、50 $\sqrt{3}$

查看试题解析
8. 如图，将△ABC绕点A逆时针旋转110°，得到△ADE ，若点D落在线段BC的延长线上，则∠B大小为（）

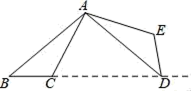A、30° B、35° C、40° D、45°

查看试题解析
9. 将等腰直角三角形AOB按如图所示放置，然后绕点O逆时针旋转90°至△A´OB´的位置．若点B的横坐标为2，则点A´的坐标为（）

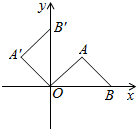A、（1，1） B、 $(- \sqrt{2} ， 2)$ C、（-1，1） D、 $(\sqrt{2} ， 2)$

查看试题解析
10. 如图，已知OA=OB=OC且∠ACB=30°，则∠AOB的大小是（）

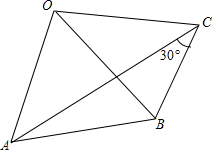A、40° B、50° C、60° D、70°

查看试题解析
11. 如图，在Rt△ABC中，∠ACB=90°， AC=3，以点C为圆心、CA为半径的圆与AB交于点D ，若点D巧好为线段AB的中点，则AB的长度为（）

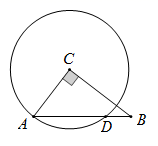A、 $\frac{3}{2}$ B、3 C、6 D、9

查看试题解析
12. 如图，两圆相交于A ， B两点，小圆经过大圆的圆心O ，点C ， D分别在两圆上，若∠ADB＝100°，则∠ACB的度数为(　　)

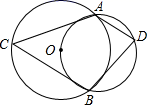A、35° B、40° C、50° D、80°

查看试题解析

二、填空题

13. 方程 $7 x = 2 x^{2} - 4$ 化为一般形式 $a x^{2} + b x + c = 0$ 后，a= ， b= ， c= ， $b^{2} - 4 a c =$ ．

查看试题解析
14. 关于x的一元二次方程 $(k - 1) x^{2} + 6 x + k^{2} - k = 0$ 的一个根是0，则k的值是．

查看试题解析
15. 若抛物线 $y = x^{2} - 2 x + m^{2} - 1$ 的顶点在x轴上，则m的值是．

查看试题解析
16. 已知二次函数 $y = - 3 {(x - 1)}^{2} + k$ 的图象上有三点A（-1， $y_{1}$ ）、B（2， $y_{2}$ ）、C（5， $y_{3}$ ），则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系为（用小于号“＜”连接）．

查看试题解析
17. 如图，E、F分别是正方形ABCD的边AB、BC上的点，BE=CF ，连接CE、DF ．若把△CDF视作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到，则旋转角的大小为．

查看试题解析
18. 如图，AB 是⊙O 的直径，C，D，E 在⊙O 上，若∠AED＝20°，则∠BCD 的度数为．

查看试题解析

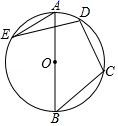
三、解答题

19. 根据要求解下列方程：

(1)、 $x^{2} + 4 x + 8 = 2 x + 10$ （公式法）；

(2)、 $2 x^{2} + 8 x - 6 = 0$ （配方法）．

查看试题解析
20. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，1），B（﹣4，2），C（﹣1，3）．

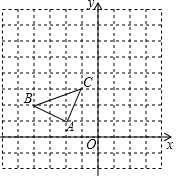
⑴作出△ABC关于y轴对称的△A₁B₁C₁ ，并写出C₁的坐标；

⑵画出△ABC绕C点顺时针旋转90°后得到的△A₂B₂C₂ ．

查看试题解析
21. 某地区2013年投入教育经费2500万元，2015年投入教育经费3025万元．

(1)、求2013年至2015年该地区投入教育经费的年平均增长率

(2)、根据（1）所得的年平均增长率，预计2016年该地区将投入教育经费多少万元

查看试题解析
22. 如图，四边形ABCD是正方形，△ADF按顺时针方向旋转一定角度后得到△ABE，点E落在AD边上，若AF＝4.AB＝7.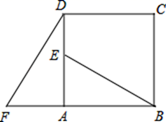

(1)、旋转中心为；旋转角度为；

(2)、求DE的长度；

(3)、指出BE与DF的关系如何？并说明理由.

查看试题解析
23. 已知二次函数 $y = - x^{2} - 2 x + 3$ 的图象与 $x$ 轴相交于 $A$ ， $B$ 两点，与 $y$ 轴交于 $C$ 点（如图所示），点 $D$ 在二次函数的图象上，且 $D$ 与 $C$ 关于对称轴对称，一次函数的图象过点 $B 、 D$ ：

(1)、求点 $D$ 的坐标；

(2)、求一次函数的解析式；

(3)、根据图象直接写出使一次函数值大于二次函数值的 $x$ 的取值范围；

查看试题解析
24. 如图，在⊙O中，AB是⊙O的弦，CD是⊙O的直径，且AB⊥CD ，垂足为G ，点E在劣弧 $\overset{⌢}{A B}$ 上，连接CE ．

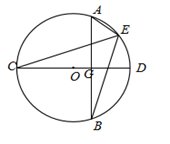(1)、求证：CE平分∠AEB；

(2)、连接BC ，若BC//AE ，求证：BC=BE ．

查看试题解析
25. 小明投资销售一种进价为每件20元的护眼台灯.经过市场调研发现，每月销售的数量y（件）是售价x（元/件）的一次函数，其对应关系如表：

x/（元/件）

22

25

30

35

…

y/件

280

250

200

150

…

在销售过程中销售单价不低于成本价，物价局规定每件商品的利润不得高于成本价的60%，

(1)、请求出y关于x的函数关系式.

(2)、设小明每月获得利润为w（元），求每月获得利润w（元）与售价x（元/件）之间的函数关系式，并确定自变量x的取值范围.

(3)、当售价定为多少元/件时，每月可获得最大利润，最大利润是多少？

查看试题解析

x/（元/件）	22	25	30	35	…
y/件	280	250	200	150	…