辽宁省沈阳市大东区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-11-24 类型:期中考试
一、单选题
-
1. 方程x2-2x=0的根是( )A、x1=x2=0 B、x1=x2=2 C、x1=0,x2=2 D、x1=0,x2=-22. 下列各组中的四条线段,能构成比例线段的是( )A、1cm,2cm,4cm,6cm B、2cm,4cm,0.4cm,7cm C、3cm,9cm,18cm,6cm D、3cm,4cm,5cm,6cm3. 用配方法解方程 时,配方后所得的方程为( )A、 B、 C、 D、4. 一元二次方程x2﹣2x﹣1=0根的情况是( )A、只有一个实数根 B、有两个相等的实数根 C、没有实数根 D、有两个不相等的实数根5. 若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )A、矩形 B、平行四边形 C、对角线相等的四边形 D、对角线互相垂直的四边形6. 小华、小强和小彬三位同学随机地站成一排做游戏,小华站在排头的概率是( )A、 B、 C、 D、17. 在△ABC中,点D,E,F分别在AB,BC,AC上,且DE∥AC,EF∥AB,若BD=2AD,则 的值为( )
 A、 B、 C、 D、8. 如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到对应的△A′B′O′.若点A的坐标是(﹣1,2),则点A′的坐标是( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到对应的△A′B′O′.若点A的坐标是(﹣1,2),则点A′的坐标是( )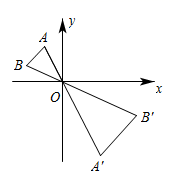 A、(4,﹣2) B、(2,﹣4) C、(﹣4,2) D、(﹣2,4)9. 如图,在菱形ABCD中,对角线AC , BD交于点O , AO=3,∠ABC=60°,则菱形ABCD的周长是( )
A、(4,﹣2) B、(2,﹣4) C、(﹣4,2) D、(﹣2,4)9. 如图,在菱形ABCD中,对角线AC , BD交于点O , AO=3,∠ABC=60°,则菱形ABCD的周长是( )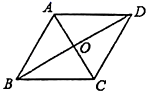 A、36 B、24 C、12 D、610. 如图,在矩形ABCD中,P为BC边的中点,E、F分别为AB、CD边上的点,若BE=2,CF=3,∠EPF=90°,则EF的长为( )
A、36 B、24 C、12 D、610. 如图,在矩形ABCD中,P为BC边的中点,E、F分别为AB、CD边上的点,若BE=2,CF=3,∠EPF=90°,则EF的长为( )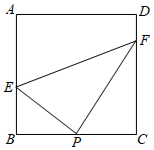 A、5 B、2 C、2 D、4
A、5 B、2 C、2 D、4二、填空题
-
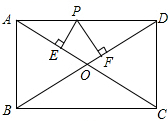
11. 已知 ,则 = .12. 两个相似三角形对应高的比为4:1,那么这两个相似三角形的面积比是 .13. 若直角三角形的两条直角边分别5和12,则斜边上的中线长为 .14. 在一个暗箱里放有m个大小相同、质地均匀的白球,为了估计白球的个数,再放入3个同白球大小、质地均相同,只有颜色不同的黄球,每次将球搅拌均匀后,任意摸出一个球记下颜色后再放回暗箱,通过大量重复试验后发现,摸到黄球的频率稳定在25%,推算m的值大约是 .15. 关于x的一元二次方程(m﹣3)x2+(2m﹣1)x+m2﹣9=0的一个根是0,则m的值是 .16. 如图,在矩形ABCD中,AB=6,AD=8,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足分别为E , F , 则PE+PF= .
三、解答题
-
17. 用公式法解方程:4x2-3=12x.18. “一方有难,八方支援”.2020年初武汉受到新型冠状肺炎影响,沈阳某医院准备从甲、乙、丙三位医生和A , B , C三名护士中选取一位医生和一名护士支援武汉.用树状图或列表法求恰好选中医生甲和护士A的概率.19. 如图,在菱形ABCD中,对角线AC , BD交于点O , E是CD中点,连接OE . 过点C作CF BD交OE的延长线于点F , 连接DF .
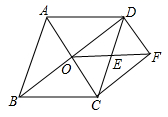 (1)、求证:四边形OCFD是矩形;(2)、若DF=2,CF=3,求菱形ABCD的面积.20. 沈阳街头随处可见单车出行,单车正逐渐成为人们喜爱的交通工具,据统计2021年某区8月份租用单车次数6400辆,10月份租用单车次数10000辆.(1)、若该区2021年8月至10月的单车租用次数的月平均增长率相同,求该区单车租用次数的月平均增长率是多少?(2)、若单车租用次数的月平均增长率保持不变,预计该区11月份单车次数租用辆.21. 如图,在平行四边形ABCD中,E是AB延长线上的一点,DE交BC于点F .
(1)、求证:四边形OCFD是矩形;(2)、若DF=2,CF=3,求菱形ABCD的面积.20. 沈阳街头随处可见单车出行,单车正逐渐成为人们喜爱的交通工具,据统计2021年某区8月份租用单车次数6400辆,10月份租用单车次数10000辆.(1)、若该区2021年8月至10月的单车租用次数的月平均增长率相同,求该区单车租用次数的月平均增长率是多少?(2)、若单车租用次数的月平均增长率保持不变,预计该区11月份单车次数租用辆.21. 如图,在平行四边形ABCD中,E是AB延长线上的一点,DE交BC于点F . (1)、求证:△DFC∽△EFB;(2)、若DC=6,BE=4,DE=8,求DF的长度.22. 小红和小丁玩纸牌优秀,如图是同一副扑克中的4张牌的正面,将它们正面朝下洗匀后放在桌面上,小红先从中抽出一张,小丁从剩余的3张牌中也在、抽出一张,比较两人抽取的牌面上的数字,数字大者获胜,请用树状图或列表法求小红获胜的概率.
(1)、求证:△DFC∽△EFB;(2)、若DC=6,BE=4,DE=8,求DF的长度.22. 小红和小丁玩纸牌优秀,如图是同一副扑克中的4张牌的正面,将它们正面朝下洗匀后放在桌面上,小红先从中抽出一张,小丁从剩余的3张牌中也在、抽出一张,比较两人抽取的牌面上的数字,数字大者获胜,请用树状图或列表法求小红获胜的概率. 23. 已知:在矩形ABCD中,AB=6,BC=3,BD的垂直平分线EF分别交AB , CD于点E , F , 垂足为O .
23. 已知:在矩形ABCD中,AB=6,BC=3,BD的垂直平分线EF分别交AB , CD于点E , F , 垂足为O .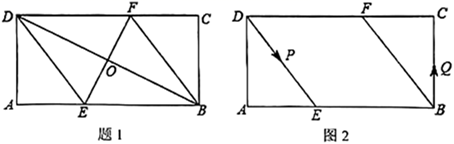 (1)、如图1,连接DE , BF .
(1)、如图1,连接DE , BF .①求证:四边形DEBF为菱形;
②直接写出AE的长 .
(2)、如图2,动点P , Q分别从D , B两点同时出发,沿 DEA和 BCF各边匀速运动一周,即点P自D→E→A→D停止,点Q自B→C→F→B停止,在运动过程中,若点P , Q的运动路程分别为x , y(xy≠0),已知A , C , P , Q四点为顶点的四边形是平行四边形,请直接写出x与y满足的数量关系式.24. 某专卖店为了清理商品库存,对原来平均每天可销售40件,每件盈利60元的商品,进行降价处理,现每件商品每降价1元,商场平均每天可多销售2件.(1)、每件商品降价多少元时,该商店日盈利可达到3150元?(2)、试问,商店日盈利能否达到3300元?若能请求出此时商品售价,若不能,请说明理由.25.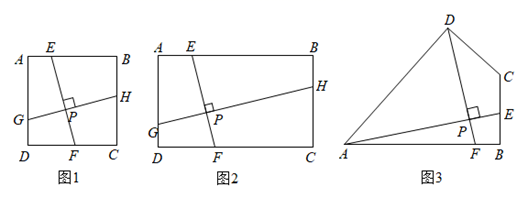 (1)、在矩形ABCD中,AB=a , BC=b , EF⊥GH于P , EF分别交AB , CD于点E , F , GH分别交AD , BC于点G , H .
(1)、在矩形ABCD中,AB=a , BC=b , EF⊥GH于P , EF分别交AB , CD于点E , F , GH分别交AD , BC于点G , H .①如图1,当a=b时,线段EF与线段GH的数量关系是;
②如图2,当a≠b时,①中的结论是否仍然成立?若成立,请说明理由,若不成立,请写出正确的结论,并说明理由;
(2)、如图3,在四边形ABCD中,BC=CD=10,∠B=∠ADC=90°,AE⊥DF于P , 点E , F分别在边BC , AB上,若 ,请直接写出AB的长.