山东省泰安市2021-2022学年七年级上学期期中数学试题
试卷更新日期:2021-11-24 类型:期中考试
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
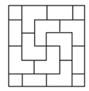 B、
B、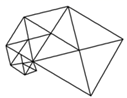 C、
C、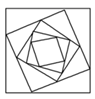 D、
D、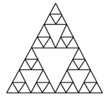 2. 如图,若 ,则 等于( )
2. 如图,若 ,则 等于( ) A、 B、 C、 D、3. 下列各组中的三条线段不能组成三角形的是( )A、3,4,5 B、4,4,9 C、5,6,6 D、5,5,14. 将一个直角三角形的三边长同时扩大10倍,得到的三角形是( )A、钝角三角形 B、锐角三角形 C、直角三角形 D、等腰三角形5. 下列关于轴对称性质的说法中,错误的是( )A、对应线段互相平行 B、对应线段相等 C、对应角相等 D、对应点连线与对称轴垂直6. 在 和 中,① ,② ,③ ,④ ,⑤ ,⑥ ,则下列( )组条件不能保证 .A、具备①②③ B、具备②④⑤ C、具备①②④ D、具备②③⑥7. 如图,以点O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画出射线OB,则∠AOB=( )
A、 B、 C、 D、3. 下列各组中的三条线段不能组成三角形的是( )A、3,4,5 B、4,4,9 C、5,6,6 D、5,5,14. 将一个直角三角形的三边长同时扩大10倍,得到的三角形是( )A、钝角三角形 B、锐角三角形 C、直角三角形 D、等腰三角形5. 下列关于轴对称性质的说法中,错误的是( )A、对应线段互相平行 B、对应线段相等 C、对应角相等 D、对应点连线与对称轴垂直6. 在 和 中,① ,② ,③ ,④ ,⑤ ,⑥ ,则下列( )组条件不能保证 .A、具备①②③ B、具备②④⑤ C、具备①②④ D、具备②③⑥7. 如图,以点O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画出射线OB,则∠AOB=( ) A、30° B、45° C、60° D、90°8. 下列各组数中,不是勾股数的是( )A、5,12,13 B、8,15,17 C、9,12,15 D、10,14,159. 如图, , ,则下面说法错误的是( )
A、30° B、45° C、60° D、90°8. 下列各组数中,不是勾股数的是( )A、5,12,13 B、8,15,17 C、9,12,15 D、10,14,159. 如图, , ,则下面说法错误的是( ) A、 垂直平分 B、 垂直平分 C、 D、10. 如图,在△ABC中,AB=10,BC=8,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN , 则线段BN的长是( )
A、 垂直平分 B、 垂直平分 C、 D、10. 如图,在△ABC中,AB=10,BC=8,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN , 则线段BN的长是( )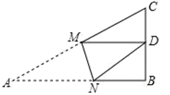 A、3 B、3.5 C、4.2 D、511. 如图的2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有( )
A、3 B、3.5 C、4.2 D、511. 如图的2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有( )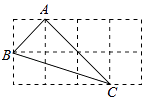 A、2个 B、3个 C、4个 D、5个12. 三个全等三角形按如图的形式摆放,则 的度数是( )
A、2个 B、3个 C、4个 D、5个12. 三个全等三角形按如图的形式摆放,则 的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 等腰三角形一个角等于100°,则它的底角是.14. 如果等腰三角形的两边长分别为7和12,则它的周长为 .15. 如图,若 , ,则 .
 16. 若三角形的边长分别为6、8、10,则它的最长边上的高为.17. 如图,OC平分∠AOB,点P是OC上一点,PM⊥OB于点M,点N是射线OA上的一个动点,若PM=5,则PN的最小值为 .
16. 若三角形的边长分别为6、8、10,则它的最长边上的高为.17. 如图,OC平分∠AOB,点P是OC上一点,PM⊥OB于点M,点N是射线OA上的一个动点,若PM=5,则PN的最小值为 . 18. 已知如图, , , 于点C , 则 .
18. 已知如图, , , 于点C , 则 . 19. 如图所示,在△ABC中,已知点D,E,F分别是BC,AD,CE的中点,且△ABC的面积为6,则△BEF的面积为.
19. 如图所示,在△ABC中,已知点D,E,F分别是BC,AD,CE的中点,且△ABC的面积为6,则△BEF的面积为. 20. 已知等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为40o , 则此等腰三角形的顶角度数为
20. 已知等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为40o , 则此等腰三角形的顶角度数为三、解答题
-
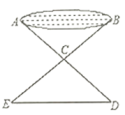
21. 如图,有一个池塘,要测池塘两端 , 的距离,可先在平地上取一个点 ,从点 不经过池塘可以直接达到点 和 ,连接 并延长到点 ,使 ,连接 并延长到点 ,使 ,连接 ,那么量出 的长度就是 , 的距离,为什么?
 22. 在讲完全等三角形后,教数学的王老师布置了一道数学题:如图所示,已知 ,其中 , ,则 与 有何位置关系?请说明理由.
22. 在讲完全等三角形后,教数学的王老师布置了一道数学题:如图所示,已知 ,其中 , ,则 与 有何位置关系?请说明理由. 23. 尺规作图:如图,某地有两个工厂M、N和两条相交叉的公路a,b现计划修建一座物资仓库,希望仓库到两个工厂的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.(保留作图痕迹).
23. 尺规作图:如图,某地有两个工厂M、N和两条相交叉的公路a,b现计划修建一座物资仓库,希望仓库到两个工厂的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.(保留作图痕迹). 24. 如图,在8×6正方形方格中,点A、B、C在小正方形的顶点上.
24. 如图,在8×6正方形方格中,点A、B、C在小正方形的顶点上. (1)、在图中画出与△ABC关于直线l成轴对称的△AB′C′;(2)、连接CC′,则线段CC′被直线l;(3)、在直线l上找一点P , 使线段PB+PC的长最短.(不写作法,保留作图痕迹)25. 绿地广场有一块三角形空地将进行绿化,如图,在 ABC中,AB=AC , E是AC上的一点,CE=5,BC=13,BE=12.
(1)、在图中画出与△ABC关于直线l成轴对称的△AB′C′;(2)、连接CC′,则线段CC′被直线l;(3)、在直线l上找一点P , 使线段PB+PC的长最短.(不写作法,保留作图痕迹)25. 绿地广场有一块三角形空地将进行绿化,如图,在 ABC中,AB=AC , E是AC上的一点,CE=5,BC=13,BE=12. (1)、判断 ABE的形状,并说明理由;(2)、求线段AB的长.26. 如图,已知 , 相交于点O , , , 过点O分别交 , 于点E、F .
(1)、判断 ABE的形状,并说明理由;(2)、求线段AB的长.26. 如图,已知 , 相交于点O , , , 过点O分别交 , 于点E、F . (1)、根据所给的条件,写出图中所有的全等三角形;(2)、请说明 的理由.27.
(1)、根据所给的条件,写出图中所有的全等三角形;(2)、请说明 的理由.27. (1)、如图1,△ABC与△ADE均是顶角相等的等腰三角形,BC、DE分别是底边.请说明:BD=CE;(2)、如图2,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE , 则∠AEB的度数为;线段BE与AD之间的数量关系是(直接写出结论);(3)、拓展探究:如图3,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE , 写出∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.
(1)、如图1,△ABC与△ADE均是顶角相等的等腰三角形,BC、DE分别是底边.请说明:BD=CE;(2)、如图2,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE , 则∠AEB的度数为;线段BE与AD之间的数量关系是(直接写出结论);(3)、拓展探究:如图3,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE , 写出∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.