山东省临沂市费县2021-2022学年七年级上学期期中数学试题

试卷更新日期：2021-11-24 类型：期中考试

进入出卷网下载

一、单选题

1. -2021的倒数是（）

A、2021 B、 $\frac{1}{2021}$ C、-2021 D、 $- \frac{1}{2021}$

查看试题解析
2. 已知a与－3互为相反数，则|－a |的值是（）

A、3 B、－3 C、±3 D、不能确定

查看试题解析
3. “浮云游子意，明月故乡情”，今年初我国向非洲国家免费提供新冠疫苗2700000支，其中2700000用科学记数法表示为（）

A、 $2.7 \times 10^{6}$ B、 $27 \times 10^{5}$ C、 $2.7 \times 10^{5}$ D、 $0.27 \times 10^{7}$

查看试题解析
4. 用四舍五入法按要求对0.7831取近似值，其中正确的是（）

A、0.783（精确到百分位） B、0.78（精确到0.01） C、0.7（精确到0.1） D、0.7830（精确到0.001）

查看试题解析
5. 下面两个数互为相反数的是（）

A、+30和﹣（﹣30） B、﹣0.2和﹣（+0.2） C、2.5和﹣[+（﹣ $\frac{5}{2}$ ）] D、+（﹣0.1）和﹣（﹣ $\frac{1}{10}$ ）

查看试题解析
6. 某交警在违规多发地段沿东西方向巡逻．若规定向东行走为正方向，该交警从出发点开始所走的路程（单位： $m$ ）分别为 $500 m$ ， $- 360 m$ ， $210 m$ ， $- 100 m$ ， $- 130 m$ ，则最后该交警距离出发点（）

A、 $1300 m$ B、 $580 m$ C、 $120 m$ D、 $300 m$

查看试题解析
7. 如图，数轴上的点A、B分别对应实数a、b，下列结论中正确的是（）

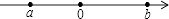A、a＞b B、|a|＞|b| C、﹣a＜b D、a+b＜0

查看试题解析
8. 已知a是相反数等于本身的数，b是倒数等于本身的数，则 $| a - 2 | - b^{2021}$ 的值为（）

A、1 B、3 C、 $\pm 1$ D、1或3

查看试题解析
9. 整式： $- 0.34 x^{2} y$ ， $π$ ， $\frac{a + 1}{2}$ ， $- 5^{2} x y z^{2}$ ， $\frac{1}{3} x^{2} - \frac{1}{5} y$ ， $- \frac{1}{3} x y^{2} - \frac{1}{2}$ 中，单项式有 $($ 　　 $)$

A、2个 B、3个 C、4个 D、5个

查看试题解析
10. 下列各组中，不是同类项的是（）

A、 $12 a^{3} y$ 与 $\frac{2 y a^{3}}{3}$ B、 $\frac{3}{2} x^{3} y$ 与－ $\frac{1}{2} x y^{3}$ C、 $2 a b x^{3}$ 与 $2 b a x^{3}$ D、 $6 a^{2} n$ 与 $- 9 a^{2} n$

查看试题解析
11. 关于整式，下列说法正确的是（　　）

A、x²y的次数是2 B、0不是单项式 C、3πmn的系数是3 D、x³﹣2x²﹣3是三次三项式

查看试题解析
12. 下面去括号正确的是（）

A、 $2 n + (- m - n) = 2 n + m - n$ B、 $a - 2 (3 a - 5) = a - 6 a + 10$ C、 $n - (- m - n) = n + m - n$ D、 $x^{2} + 2 (- x + y) = x^{2} - 2 x + y$

查看试题解析
13. 计算： $1 - (+ 2) + 3 - (+ 4) + 5 - (+ 6) + \dots - (+ 2022) =$ （）

A、2022 B、-2022 C、-1011 D、1011

查看试题解析
14. 观察下列等式： $7^{1} = 7$ ， $7^{2} = 49$ ， $7^{3} = 343$ ， $7^{4} = 2401$ ， $7^{5} = 16807$ ， $7^{6} = 117649$ ，…，那么： $7^{1} + 7^{2} + 7^{3} + \dots + 7^{2020}$ 的末位数字是（）

A、9 B、7 C、6 D、0

查看试题解析

二、填空题

15. 用“>”或“<”填空： $- \frac{5}{6}$ $- \frac{4}{5}$

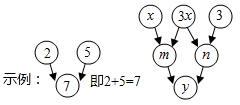
查看试题解析
16. 若 $3 a^{m} b^{2}$ 与﹣2a³bⁿ是同类项，则m+n＝．

查看试题解析
17. 已知 $a^{2} + 2 a = 5$ ，则 $2 a^{2} + 4 a - 2$ 的值为．

查看试题解析
18. 若 $| a | = 3$ ， $| b | = 4$ ，且 $a$ ， $b$ 异号，则 $| a + b | =$ ．

查看试题解析
19. 式子 $- 6 + | x + 2 |$ 的最小值为．

查看试题解析
20. 如图，约定：上方相邻两数之和等于这两个数下方箭头共同指向的数．当 $y = 17$ 时， $n$ 是．

查看试题解析
21. 黑、白两种颜色的正六边形地砖按如图所示的规律拼成若干个图案：则第n个图案中有白色地砖块．（用含n的代数式表示）

查看试题解析

三、解答题

22. 计算：

(1)、 $- (- 4) + (- 1) - (+ 5)$

(2)、 $\frac{5}{2} \div (- \frac{5}{6}) \times (- \frac{1}{3})$

(3)、 $- 1^{4} + | 5 - 8 | + 27 \div (- 3) \times \frac{1}{3}$

(4)、 $(\frac{1}{3} - \frac{5}{6} + \frac{3}{4}) \times (- 36)$

查看试题解析
23. 先化简，再求值： $\frac{1}{3} (6 x^{2} - 9 x y) - (x^{2} - x y) + (y^{2} - x^{2})$ ，其中 $x = 2$ ， $y = - 1$ ．

查看试题解析
24. 已知A＝3x²+y²﹣2xy ， B＝xy﹣y²+2x² ，求：

(1)、2A﹣3B；

(2)、若|x+2|+（y﹣3）²＝0，求2A﹣3B的值．

查看试题解析
25. 如图，数轴上的三点A、B、C所对应的数分别为a、b、c ．

(1)、填空： $a － b$ 0； $a + c$ 0； $b + c$ 0．（填“＞”“＜”或“＝”）

(2)、化简：丨 $a － b$ 丨－丨 $a + c$ 丨+丨 $b + c$ 丨．

查看试题解析
26. 阅读材料：我们知道， $4 x - 2 x + x = (4 - 2 + 1) x = 3 x$ ，类似地，我们把 $(a + b)$ 看成一个整体，则 $4 (a + b) - 2 (a + b) + (a + b) = (4 - 2 + 1) (a + b) = 3 (a + b)$ ．“整体思想”是中学数学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．尝试应用整体思想解决下列问题：

(1)、把 ${(a - b)}^{2}$ 看成一个整体，合并 $3 {(a - b)}^{2} - 6 {(a - b)}^{2} - 2 {(a - b)}^{2}$ ；

(2)、已知 $x^{2} - 2 y = 4$ ，求 $3 x^{2} - 6 y - 11$ 的值；

(3)、已知 $a - 2 b = 2$ ， $2 b - c = - 5$ ， $c - d = 10$ ，求 $(a - c) + (2 b - d) - (2 b - c)$ 的值．

查看试题解析